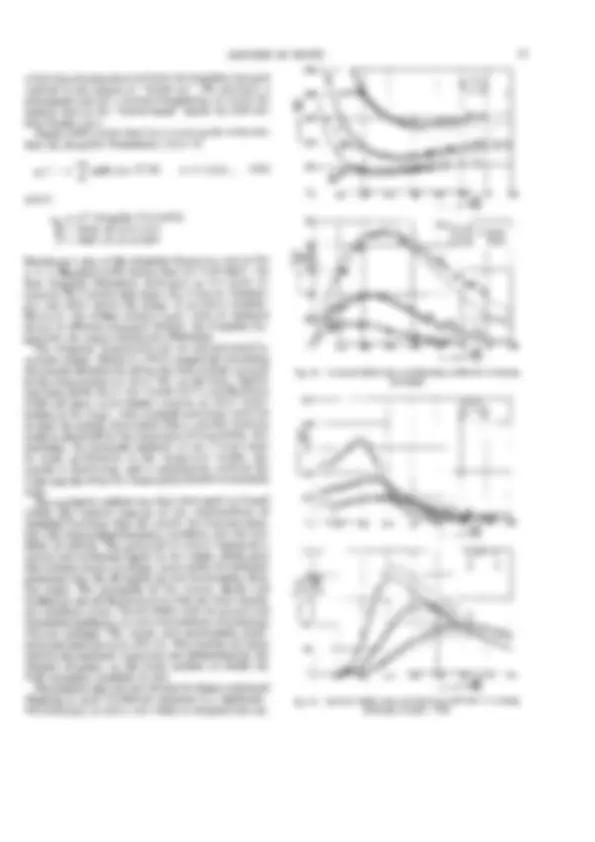
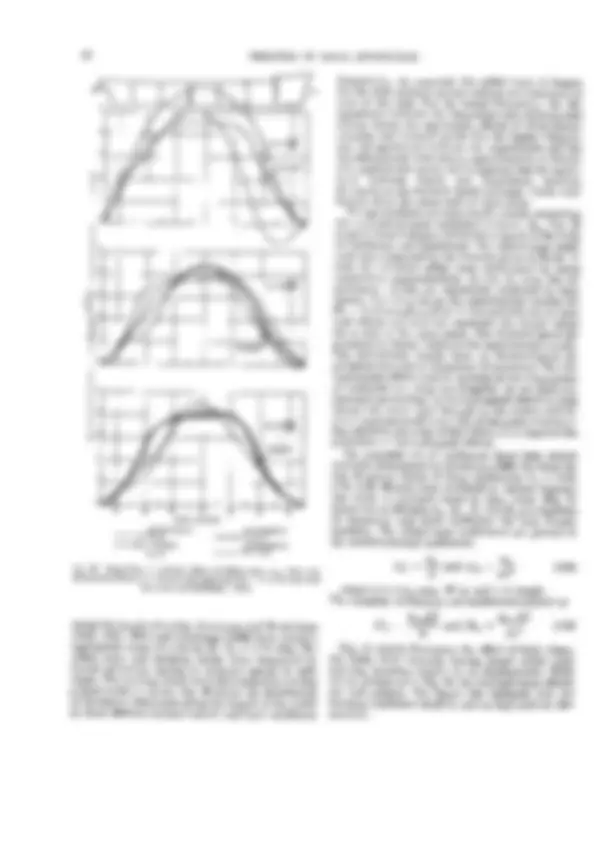
Pré-visualização parcial do texto
Baixe Principles Of Naval Architecture Vol III - Motions in Waves and Conttrollability e outras Notas de estudo em PDF para Engenharia Naval, somente na Docsity!
Volume III « Motions in Waves and Controllability Edward V. Lewis, Editor Published by The Society of Naval Architects and Marine Engineers 601 Pavonia Avenue Jersey City, NJ Copyright & 1989 by The Society of Naval Architects and Marine Engineers. Tt is understood and agreed that nothing expressed herein is intended or shall be construed to give any person, firm, or corporation any right, remedy, or claim against SNAME or any of its officers or members. Library of Congress Catalog Card No. 8860829 ISBN No. 0939773023 Printed in the United States of America First Printing, November, 1989 PREFACE (22401b), which numerically is 1.015 x metric ton. Power is usually in kilowatts (1 kW = 1.34 hp). A conversion table also is included in the Nomenclature at the end of each volume The first volume of the third edition of Principles of Naval Architecture, com- prising Chapters I through IV, deals with the essentially static principles of naval architecture, leaving dynamic aspects to the remaining volumes. The second vol- ume consists of Chapters V Resistance, VI Propulsion and VII Vibration, each of which has been extensively revised or rewritten. Volume III contains the two final chapters, VIII Motions in Waves and IX Controllability. Because of important recent theoretical and experimental devel- opments in these fields, it was necessary to rewrite most of both chapters and to add much new material. But the state-of-the-art continues to advance, and so extensive references to continuing work are included. November 1989 Edward V. Lewis Editor Table of Contents Volume III Page Page Preface ......n.ocis ii icsitesecrereereren ii Acknowledgments..........csi iii vi Chapter 8 (VII) MOTIONS IN WAVES ROBERT F. BECK, Professor, University of Michigan; WILLIAM E, CUMMINS,** David Taylor Research Center; JOHN F. DALZELL, David Taylor Research Center; PHILIP MANDEL,* and WILLIAM C, WEBSTER, Professor, University of California, Berkeley 1. Introduction. 1 5. Derived Responses .... 2. Ocean Waves 3 6. Control of Ship Motion 8. Ship Responses to Regular Waves 41 7. Assessing Ship Seaway Performance 137 4. The Ship in a Segway... Ba 8 Design Aspects.... css 160 References . 177 Nomenelature 188 Chapter 9 (IX) CONTROLLABILITY C. LINCOLN CRANE,** Exxon Corporation; HARUZO EDA, Professor, Stevens Institute of Technology: ALEXANDER €. LANDSBURG, U.S. Maritime Administration 1. Introduction 191 9. Theoretical Prediction of Design 2. The Control Loop and Basic Coefficient and Systems Equations of Motion ................ 192 Kentification ..........c oie 3. Motion Stability and 10. Accelerating, Stopping and Backing. Linear Equations... 195 11, Automatic Control Systems . 4. Analysis of Course Keeping— 12. Effects of the Environment. Controls-Fixed Stability . 13. Vessel Waterway Interactions. 5. Stability and Control... 14. Hydrodynamies of Control Surfaces... 6. Analysis of Turning Ability . 15. Maneuvering Trials and Performance 7. Free Running Model Tests Requirements 316 and Hydraulic Models ............... 215 16. Application to Design .. =... B2T 8. Nonlinear Equations of Motion 17. Design of Rudder and Other Control and Captive Model Tests ............ 21 Devices. .....ceceeeemeseseeeeseeeees References .... Nomenclature . General Symbols 421 Index... 424 * Now retired ** Deceased Note: The office affiliations given arc those at the time of writing the chapters. John F. Dalzeil, Philip Mandel Robert F. Beck, William E. Cummins William €C. Webster CHAPTER VIII Motions in Waves Section 1 Introduction ' 1.1 Ship motions at sea have always been a problem for the naval architect. His or her responsibility has been to insure not onty that the ship can safely ride out the roughest storms but that it can proceed on course under severe conditions with a minimum of delay, or carry out other specific missions successfully. However, the problem has changed through the years. Sailing vessels followed the prevailing winds—Colum- bus sailed west on the northeast trades and rode the prevailing westerlies farther north on his return voy- ages. The early clipper ships and the later grain racers from Australia to kurope made wide detours to take advantage of the trade winds. In so doing they made good time in spite of the extra distance travelled, but the important fact for the present purpose is that they seldom encountered head seas. With the advent of steam, for the first time in the history of navigation, ships wcre able to move directly to windward. Hence, shipping water in heavy weather caused damage to superstructures, deck fittings and hatches to increase, and structural bottom damage near the bow appeared as a result of slamming. Strue- tural improvements and easing of bottom lines for- ward relieved the latter situation, and for many years moderately powered cargo ships could use full engine power in almost any weather, even though speed was reduced by wind and sea. The same is true even today for giant, comparatively low-powered tankers and many dry-bulk carriers. For many years the pilot charts issued by the US. Navy Oceanographie Office still showed special routes for “low-powered steamers” to avoid head winds and seas. It should be emphasized that the routes shown for the North Atlantic, for example, did not involve avoiding bad weather as such, for eastbound the routes for low and high-powered steamers were the same; but they did attempt to avoid the prevailing head winds 'This section written by the editor. and head seas westbound that greatly reduced the speed of low-powered ships. The situation is different for today's modern fast passenger vessels and high-powered cargo ships. In really rough head seas, their available power is ex- cessive and must be reduced voluntarily to avoid ship- ping of water forward or incurring structural damage to the bottom from slamming. Hence, maintaining schedule now depends as much on ship motions as on available power, Similarly, high-powered naval vessels must often slow down in rough seas in order to reduce the motions that affect the performance of their particular mission or function—such as sonar search, landing of aireraft or helicopters and convoy escort duty. Furthermere, new and unusual high-performance craft—compara- tively small in size—have appeared whose perform- ance is even more drastically affected by ocean waves. These include high-speed planing craft, hydrofoil boats, catamarans and surface effect ships, most but not all being developed or considered for military uses. A very different but related set of problems has arisen in the development of large floating structures and platforms that must he towed long distances and be accurately positioned in stormy seas for ocean-drill- ing and other purposes. As seakeeping problems have thus became more se- rious, particularly for the design of higher-speed oceangoing vessels, rapid expansion began in the mid- 1950s in the application of hydrodynamic theory, use of experimental model techniques and collection of full. scale empirical data. These important developments led to a better understanding of the problems and ways of dealing with them. Along with remarkable advances in oceanography and computer technology, they made it possible to predict in statistical terms many aspects of ship performance at sea. Furthermore, they could be applied to the seagoing problems involved in the design of the unusual new high-speed craft and float- ing platforms previously mentioned. 2 PRINCIPLES OF NAVAL ARCHITECTURE in view of the increasing importance of theoretical approaches to seakecping problems, it is fe to be essential to cover in this chapter in a general way the basic hydrodynamie principles and mathematica! tech- niques involved in predicting ship molions in both reg- ular and irregular seas (Sections 2, 3 and 4). Some readers may wish to proceed directly to Sections 5-8, which discuss more practical aspects of ship motions and the problems of design for good seakecping per- formance. The understanding of ship motions at sea, and the ability to predict the behavior of any ship or marine structure in the: design stage, begins with the study of the nature of the ocean waves that constitute the environment of the seagoing vessel. The outstanding characteristic of the open ocean is its irregularity, not only when storm winds arc blowing but even under relatively calm conditions. Oceanographers have found that irregular seas can be described by statistical mathematics on the basis of the assumption that a large number of regular waves having different lengths, directions, and amplitudes are linearly super- imposed. This powerful! concept is discussed in Section 2 of this chapter, but it is important to understand that the characteristics of idealized regular waves, found in reality only in the laboratory, are also fun- damental for thc description and understanding of re- alistic irregular seas. Conseguently, in Section 2—after a brief discussion of the origin and propagation of occan waves—the theory of regular gravity waves of simple form is presented. Mathematical models describing the com- plex irregular patterns actually observed at sea and encountered by a moving ship are then discussed in some detail. The essential feature of thesc models is the concept of a spectrum, defining the distribution of energy among the different hypothetical regular components having various frequencies (wave lengths) and directions. It is shown that various sta- tistical characteristics of any seaway can be deter- mined from such spectra. Sources of data on wave characteristics and spectra for various oceans of the world arc presented. It has been found that the irregular motions of a ship in a seaway can be described as the linear super- position of the responses of the ship to all the wave components of such a seaway. This principle of su- perposition, which was first applicd ta ships by St. Denis and Pierson (1953),* requires knowledge of both the sea components and the ship responses to them. Hence, the vitally important linear theory of ship motions in simple, regular waves is next developed in Section 3. It begins with the simple case of pitch, heave and surge in head seas and then goes on to the general case of six degrees of freedom. The equations of mo- “Complete references are listed at end of chaper tion are presented and the hydrodynamie forces cval- uated on the basis of potential theory. The use of strip theory is then described as a convenient way to per- form the integration for a slender body such as a ship. Finally, practical data and experimental results for two cascs are presented: the longitudinal motions of pitch-heave-surge alone, and lhe transverse motions of roli-sway-yaw. In Section 4 Lhe extension of the problem of ship motions to realistie irregular seas is considered in de- tail, the object being to show how modern techniques make it possible to predict molions of almost any type of craft or floating structure in any seaway in prob- ability terms. It is shown that, knowing the wave spce- trum and the characteristic response of à ship to the component waves of the irregular sca, à response spec- trum can be determined. From it various statistical parameters of response can be obtained, just as wave characteris are obtainable from wave spectra. Re- sponses to long-erested seas are treated first, and then the more general case of short-crested seas. Particular attention is given to the short-term statistics of peaks, or maxima, of responses such as pitch, heave and roll; both motions and accelerations. Examples of typical calculations are included. Section 5 considers the prediction of responses other than the simple motions of pitch, heave, roll, etc. These so-valled derived responses include first the vertical motion (and velocity and acceleration) of any point in a ship as the result of the combined effect of all six modes, or degrees of freedom. Consideration is given next to Lhe relative motion of points in the ship and the water surface, which leads to methods of calculating probabilities of shipping water on deck, bow emergence and slamming. Non- linear effects come in here and are discussed, along with non-linear responses such as added resistance and power in waves. Finally, various wave-induced loads onaship's hull structure are considered, some of which also involve non-linear effects. Section 6 discusses the control of ship motions by means of various devices. Passive devices Lhat do not require power or controls comprise bilge keels, anti- rolling tanks and moving weights. Five performance criteria for such devices are presented, and the influ- ence of each is shown by calculations for a ship relling in beam seas. Active devices, suth as gyroscopes, con- trollable fins and controlled rudders are then dis- cussed. Section 7 deals with criteria and indexes of sea- keeping performance. Tt is recognized that, in order for new designs to be evaluated and their acceptability determined, it is essential to establish standards of performance, just as in other chapters where criteria of stability, subdivision and strength arc presented. Various desirable features of ship behavior have been listed from time to time under the heading of seakindiiness. These include easy motions, (i.c., low 4 PRINCIPLES OF NAVAL ARCHITECTURE to review the physical processes of storm wave gen- eration and of wave propagation in a general way Storm waves arc generated by the interaction of wind and the water surface. There are at lcast two physical processes involved, these being the friction between air and water and the local pressure fields associated with the wind blowing over the wave sur- face. Although a great deal of work has been done on the theory of wave generation by wind, as piunmarized by Korvin-Kroukovsky (1961) and Ursell (1956), completely salisfactory mechanism has yet been de. vised to explain the transfer of encrgy from wind to sea. Nevcrtheless, it seems reasonable to assume that the total storm wave system is the result of many local interactions distributed over space and time. These events can be expected to be independent unless they are very close in both space and time. Each event will add a small local disturbance to the existing wave system. Within the storm area, there will be wave interac- tions and wave-breaking processes that wil] affect and limit the growth and propagation of waves from the many local disturbances. Nevertheless, wave studies show that if wave amplitudes are small the principle of linear superposition governs the propagation and dispersion of the wave systems outside the generating area. Specifically, if (x,y, t) and £áa, yy t) are two wave systems, L( Lx, y, t) is also a wave system. This implies that one wave system can move through another wave system without modification. While this statement is not absolutely true, it is very nearly so, except when the sum is steep enough for wave breaking to oceur, A second important characteristic ol water waves that affcets the propagation of wave systems is that in deep wator the phase velocity, or celerity, of a sim- ple regular wave, such as can be generated in an esx- perimental tank, is à function of wavelength. Longer waves Lravel faster than shorter waves. Study and analysis of ocean wave records has shown that any local system can be resolved into a sum of component regular waves of various Jengths and directions, using Fourier Integral techniques. By an extension of the prineiple of superposition, the subsequent behavior of the sum of these component regular wave systems will determine the visible system of waves, Since these component waves have different celeritics and direc- tions, the propagating pattern will slowly change with time. If the propagating wave system over a short period of time is the sum vuf a very large number of separate random contributions, all essentially independent, the surface elevation is Ur y = gt) [e and the laws of statisties yield some very uscful con- clusions. Since water is incompressible, the average value of vertical displacement at any instant, £ in a regular component wave, é, is zero 61 it is assumed to be of sinusoidal form, as discussed subsequently), and thercforc the average valuc for the wave system, Cry 8) zero. However, the variance (or mean square deviation from the mean) of £,, which is the average value of 2, wrilten (12), is a positive quantity that measures the severity of the sea. A fun- damental theorem of statisti ates that the variance of the sum of a set of independent random variables tends asymptotically to the sum of the variances of the component variables. Thus, for a very large (infi nite) number of components, assumed to be indepen- dent, =2 43 (2 A final statistical conclusion is a consequence of the central limit theorem of statistics. In the case under discussion, this theorem implies that L(2, y, t) willhave a normal (or Gaussian) density function, even if the component variables ils, y £) are not distributed nor- mally. The importance of this result is that the density function of a normal random variable is known if its mean and variance are known. Therefore, if the vari- ance of the surface elevation in the multi-component wave system can be estimated, its probability density as a random variable is known. Ochi (1986) deals with the analysis of non-Gaussian random processes. These conclusions from the laws of statistics all di pend upon the previously mentioned principle of su- perposition, which holds approximately but not absolutely for water waves, and on the assumption of independence of component waves. Therefore, the con- clusions themselves are approximate and this should be remembered. However, it has been found that over the short term, deviations become significant only when the waves are very steep, and even then pri- marily in those characteristies that arc strongly influ- enced by the crests. lt will be shown that the short-term deseriptive model that has been described leads to a mathematical technique for describing the irregular sea at a given location and time, while conditions remain steady or stationary. Each sea condition can for short periods of time be as unique as a fingerprint, and yet, as with a fingerprint, it has order and pattern, as defined by its directional spectrum, to be explained subsequently (Section 2.6). However, since the wind velncities and directions are continually, albeit slowly, changing, the short-term mathematical description will also change. Hences, à broader model is also needed to cover large variations in time, involving wind effects on growth and decline of local wave systems, as well as propa- gation and dispersion. Fig. 1(a) symbolizes a storm-wave generation area. It may be assumed that disturbances are being gen- erated by the interaction of the wind and sea surface throughout the storm area from the time the wind MOTIONS IN WAVES 5 FETCOH —— £ & L,/2), 2 =g/k=g9Ld2m (10) For many problems the most important aspect of waves is the distribution of pressure below the surface. It is convenient to compute the pressure relative to horizontal lines of constant pressure in still water. The elevation £ of lines of equal pressure in a wave relative to the still-water pressure lines, Fig. 2, is obtained from the expression 106 got which is derived in hydrodynamies texts (Lamb, 1924) by means of Bernoulli's theorem for a gravity force acting on a body of fluid under uniform atmospheric pressure, assuming that wave height is small (strictly speaking, infinitesimal). Then for water of any depth - KEV? cosh k(z + À) g sinh kh Since from Equation (8) AV2/g = tanh kh, this can be simplified to — +cosh(z + h) t=. cosh kh In deep water (large A) the ratio cosh k(z + k)/ cosh kh approaches e“, and L=Le“cosk(tr— Vt) These expressions show that contours of equal pres- sure at any depth are cosine curves which are functions of time when observed at a fixed point x, or a function of distance 4 at a particular instant t,. Since e” de- creases as z decreases, the contours of equal pressure are attenuated with depth, approaching zero amplitude as z —> — ce, These contours are the same as those generated by the orbital motions of individual parti- cles. To obtain the surface wave profile, z is taken equal to zero in Equation (13) or (14). Then ty = Tocos kr — Vit) for both deep and shallow water. A more convenient form for the equation of a simple harmonic wave can be obtained by using circular fre- quency w = 27/7T,. The period T. is the time required for the wave to travel one wave length, and hence the relationship between wave length and period in deep water can be derived from Equation (10). aa Sine - (o) a a) cos k(x — Vt) (12) £ cos (x — V.) (13) (14) (15) (16) FT, 7 IN WAVES 7 Hence, circular frequency 2êm ( 2m ) (7.7 9 Te to = E cos (kz — wi) When observed at a fixed point, with yz = O = (gt = kV. (M o and as to =T cos(— at) = É cos vt Alternatively, if the wave profile is studied at t = O lo = Tocos kz The slope of the wave surface is obtaincd by difler- entiation: dh = kl sin ky (19) The slope is maximum when kx = w/2 and sin kx = 10. Then dt, Loma Max = L = LT where A, is the wave height from hollow to crest. This maximum slope occurs midway between a crest and a hollow. The contours of constant pressure that have been derived in Equations (13) and (14) also indicate the increase or decrease in pressure relative to still water at any point in terms of depth or head. Hence, to obtain the pressure p at any point we need only multiply the head by density pg, or p=pgioz+ O In deep water, then, from Equations (11) and (14) = ki 2 (20) --pgz + Epge” cos (kz — wi) As previously noted, z should be measured to the cen- ter of the circular path described by the particle at the point in question. Evaluation of the equation for pressure in a deep- water wave under the crest, at 2% below the original stillwater level (2 = —2£), gives, for example p= —pyt-25) + Epgoti = plo(2 + 2%) and for k = 0.015, and É = 10, for example: p= pig(2O + 074) = plg(278) If the pressure were directly proportional to depth below the surface, it would be p$ 9(3.0) at this point. The difference represents the so-called Smith efect (Smith, 1883). Similarly, under the wave hollow at a depth of 2E below still-water level (2 = —28), p = pEg(20 — 0.74) = plg(1.26) instead of pZg(1.0). Thus under the crest the pressures 8 PRINCIPLES OF NAVAL ARCHITECTURE are decreased, and under the hollow the pressures are increased, by the Smith effect. The energy in a train of regular waves consists of Kinetic energy associated with the orbital motion of water particles and potential energy resulting from Lhe change of water level in wave hollows and crests. The kinetic energy can be derived from the velocity potential. For one wave length L, the kinetic energy per unit breadth of a wave of small height is given im books on hydrodynamies (Lamb, 1924; Korvin-Krou- kovsky, 1961), as “4 4 CP fog This is evaluated for a simple cosine wave as “pgLy The potential energy due to the elevation of water in one «ave length is obtained by taking static moments about the still-water level, À unit increment of area is tdx and the lever arm is &,/2. Hence, integrating, potential energy is polia! 2Xadr a = em [ gar For a cosine wave, W=TEcosktg-— Vt) andatt = 0 s— É cos kr Hence, potential energy is AE pgL, These derivations show that wave energy is half kinetie and half potential when averaged over a wave length. Total energy is da PE E Or the average energy per unit area of surface, Y pot* (21) Another useful! property of waves, especially irreg- ular waves to be discussed in Section 2.6, is the var- iance, or the mean-square value of surface elevation as a function of time, In general, the variance of a continuous function with zero mean is given by, Ave. unit Energy [qr = Lim 7| Tom TD qa where the brackets ( ) indicate mean value of, In the case of a simple harmonic wave, as given by Equation (18) at x = 0, T can be taken as the wave period, and it can be shown that CU) Elo de (22) O) = nt? (23) That is, the variance of wave elevation of a single cycle of a sine wave is equal to onc-half the square of the amplitude. This theorem is also true for a finite number of complete eycles, or in the limit as 7 — «s in Equation (22). For the work ta follow, the two-dimensional regular wave can be considered to be a three-dimensional wave train with straight, infinitely long crests, i.e., a long- crested regular wave. Furthermore, with axes fixed in the earth the surface elevation of such waves traveling at any angle, qu, to the x-axis can be described by the gencral equation, tlr, y t)= E cos [k(xeos p (24) where e is a phase angle. For the case q = O this equation reduces to Equation (18), except for the phase angle, which is needed when more than one wave is present. If a fixed point at the origin is considered (x = 0, y = 0), the equation becomes tt) = É cos (— (25 Wave Properties. The following is a summary of the properties of two-dimensional harmonic waves and waves of finite height in deep water (any consistent units): + gysing) — vt + € ot + e) Wave number k=27/L.= w'lg Surface profile = L cos k(x — Vá) (15) (first approxima- o tion) so cos (kz — wt) (18) Velvcity potential = —LVe” sin ktr — o (4 - (E) 8 Sh 9 2a e o Wave celerity T (10) o VE gTE Wave length besta = (16) Wave period Te= (EoLlg)? 06) Maximum wave 7 h slope (first ap- kE = 27 É. — Thy proximation) Leo Ls (20) Wave energy per - unit area upg é! (21) Wave variance (M=tr (23) In feet-seconds units: Wave celerity V. = 2.26L, is often taken to represent the complex amplitude, in which case the imaginary part defines the phase angie and is unnecessary. 10 PRINCIPLES OF NAVAL ARCHITECTURE E RADIUS OF ROLLING CIRCLE. SEE FIG.5 + DIRECTION OF WAVE ADVANCE dr conreseonons | t- I Eve SATER A VOLUME SUCH AS ABCD IN STILL WATER IS DISTORTED ÁS ABCD IN WAVE WATER Fig. 4 Trochoidal wave motion TRACK OF ROLLING CIRCLE T T r Fig. 5 Geomery of trochoid If we call the orbit radius 7 and the amplitude £, then é = , Quantities referring to the surface wave are denoted by subseript O; Lhus É = r;. If R is the radius of the rolling circle and L,. is the wave length from crest to crest, L, = 27R. To draw a Lrochoidal- wave surface, the selected wave length is divided by a convenient number of cqually spaced points, and, with each as a center, a circle of diameter equal to the selected wave height is described. In these cireles are drawn radii at successive angles which increase by lhe same fraction of 360 deg as the spacing of the circles in relation to wave length, The curve connecting the ends of those radii is the desired trochoid. In Fig. 5, an ordinate z upward, and an angular velocity w counterclockwise, are considered positive. Prom an initial position, shown at the left, the large circle is assumed to be rolling steadily, counterclock- wise, and after time t to have reached the position OCP, having turned through the angle 8 = ct. In this case 8 is positive since o is counterclockwise. The parametric equations of the trochoid in Fig. 5 are x— RO +rsin6=Reottrsnawt! z=R+rcs6=R-rcos ut (28) The radii of the circles in which the particles move decrease exponentially with depth; that is, as in the case of the harmonie wave r= res where r, is the radius of a particle at the surface, and * is measured to the center of the circle in which the particle moves. The twochoidal wave is somewhat sharp im the crest and flat in the trough like a simple wave in a model tank, and like the Stokes wave, Fig. 3. Consequently, for equal water volumes the lines of orbit centers must be somewhat above the corresponding still-water lev- els in order that the amount of water in the crest will equal the amount removed in the hollow. Tt can be shown that this rise of orbit centers is »2/2R, Pig. 4. Although the trochoidal wave is reasonably realístic for waves up to about £,/20 in height, the limiting case of R = » gives un impossibly sleep wave with very sharp cusps. Other characteristics of the trochoidal wave, such as velocity, period, pressure change with depth, are the same as for the simple harmonie wave previously discussed, Obviously the pressure at any point-on the surface of a wave is atmospheric. Furthermore, the sum of all the hydrodynamic and buoyant forces acting on a sur- face particle is perpendicular to Lhe surface, as dem- onstrated by Froude with a little float carrying à pendulum. Although this statement can be proved on the basis of the theory of a simple harmonic wave, it is most easily demonstrated by means of trochoidal theory. Following Froude's approach, it is convenient to deal with the inertial reactions to the water-pressure (orces acting on the particle P in Fig. 6, although the latter could aiso be determined directly. Às previously shown, the buoyancy and hydrodynamic pressure forces in the wavc cause the particle to move in a circular path, and the equal and opposite reactions consist of gravity mg acting downward and a centrif- ugal reaction QF" resulting from orbital motion of the particle mrw? it can be shown that in a trochoidal gravity wave q” = q/R and therefore the centrifugal reaction is mg(r/R) The resultant is PF in Fig. 6, In triangles QCP and F'FP, PF“ is in line with QP and F"F is parallel to QC. Also r r Cid = (ima a)/ 19 ROO o PF Fr MOTIONS IN WAVES NM c I £ x R No mesuitant PRESSURE ! N FORCE F Fig. 6 Inertial reactions on water particle in trochoidol wave Hence the two triangles are similar and PF, the resultant, is in line with CP and normal to the tro- choidal surface. Any particle in the surface is acted upon, therefore, by a resultant pressure force which is normal to the surface. The net wave pressure force on the particle is equal and opposite to PF. Since no tangential force exists, the surface must be one of equal pressure, 2.5 Compound Gravity Waves. The highly idealized simple harmonie regular wave provides the hydrody- namie basis for short-term stochastic models of ocean waves, but its physical existence is for practical pur- poses limited to the laboratory. As described in Section 2.1, natural waves may usually he considered to be sums of many independent regular waves—or surface disturbances which can Lhemselves be treated as sums of simple regular waves. Before treating these sto- chastic models, it is useful to consider several com- pound wave systems that exhibil important physical effects, even though they are just as idealized as lhe regular progressive wave. (a) Standing Waves. Suppose we superimpose two regular waves of the samc amplitude and period, but travelling in opposite directions. From Fiquation (18) the sum of surface elevations can be written ta, t) = É [eos (kz — et) + cos (kr + wt)] = 2E cos ke cos wt (29) When t = 0, Tu 27, - -, the wave form is a cosine curve with crests at ), Lis 2Lao + When t = UT To + - - the form is the negalive of the first form, with troughs ata = 0, Lu, ++ Whent= à Ta, Y To, the surface is completely flat. At inter- mediate times, the surface has the samc shape as at £ = 0, but with amplitude 2Z cos wt. Thus, the crests never move but decrease in place and become troughs after passing through zero. This is known as a stand- ing wave. By adding the velocity potentials of the two component progressive waves, it can be shown that the particle velocity at « = 0 is always vertical, and ata = L/4,3L,/4, + - -, (the nodes), the velocity is always horizontal. Therefore, the wave form is the same as it would be if a wall were placed at x = 0, and, in fact, a standing wave is gencrated when a progressive regular wave is reflected from a vertical wall perpendicular to its direction of advance. (b) Wave Groups. Itis frequently observed that natural waves may appear to exist in packets or groups, with relatively calm patches between groups. In effect, the waves have an envelope that ilself rises and falls with time and distance. This phenomenon is particularly characteristic of swell waves and is of importance in wave propagation. An idealized wave group pattern can be simulated by a sum of two progressive waves of the same am- plitude but with slightly different frequencies, moving in the same direction. Thus, te, t) = E [cos (k, « — wt) + cos (kr — «a,)] = 2E cosllk, + foz — (ot mt] tky oz — (6; — ot] (30) The first cosine factor in this equation has the form of a progressive regular wave with wave length Le = 2m/hlk, + ko) , cos or, 1 1 1 - L L, a Thus, the wavelength of this factor is the harmonie mean of the wavelengths of the two components. The factor is multiplied by another cosine factor with wave- length, L,= êm/iuth, ko) and period T, = 27! ey — 6%) Since k, and k, have been considered to be nearly equal, the wavelength of this factor is very large com- pared with the wavelength of the first cosine factor. Therefore, it bchaves like an envelope slowly advane- ing. It has the velocity, MOTIONS IN WAVES 13 d is taken to be very small, See Fig. 8. More important than the component amplitudes, however, is the total variance of the wave system, usually designated E, which is a good measure of the severity of the sea. E = UM) The components on the right-hand side of (33) have been assumed to be independent random variables by virtue of their random phases. Since, as noted in Sec- tion 2.1, the variance of the sum of a large number of independent random variables approaches the sum of the variances of these variables, Equation (2) gives E= (UN) =D?) or integrating Equation (34) and substituting, E= r So) do em That is, the area under the spectrum is equal to the variance, E, of the wave system. Referring to the typical plot of a variance spectrum ata point (Fig. 8), the areas of the elemental rectan- gles, S(w;) 8w, may be seen from (34) to define the variances of the wave components: Strietly speaking, the foregoing interpretation of the spectrum in terms of component waves is valid only for the limiting case da — O and the number of components — «o. By Equation (36) the elemental rectangles also define the amplitudes of the components in the limit. How- ever, when a large number of components is assumed, say 15 or 20, a fair finite-sum model of a unidirectional (long-crested) sea is obtained. (A multi-directional, short-crested, sea requires many more). Since any par- ticular rectangle represents the variance in that band of frequencies, a wave of the indicated finite amplitude would have the same variance as the infinite number of components within that band. Hence, the algebraic addition of these 15 or 20 component waves, shown at the bottom of Fig. 8, will give a pattern that has the same total variance and closely resembles the record from which the spectrum was obtained. Tt will also have many of the same statistical properties. However, we can never match the record exactly, no matter how many components are assumed, for although an arti- ficial wave can be made to repeat itself, a real ocean wave record never does so. This is actually no handi- cap, for it is statistical information that we ultimately need for application to ship design. It is of interest to plot five or more sine curves through several eyeles and to add successive ordinates algebraically or to carry out the same procedure on an electronic computer. The resulting curve will dem- onstrate clearly that the sum of even a small number of regular sine waves is an irregular pattern, provided that the component waves are in random phase. it should be emphasized that the component waves are not directly visible either at sea or in a wave record. However, the variance spectrum defining these com- ponents can be obtained from a wave record by ap- plying the techniques of generalized harmonie analysis (Wiener, 1930, 1949), provided that the record is long enough (15 to 20 min) and that sea conditions remain steady. Such records have been obtained mainly by means of shipborne recorders aboard stationary ves- sels (such as wcather ships). Airborne laser and radar scanning have also been used, and radar altimeters on spacecraft are under development (Pierson, 1974). Tn the analysis procedure developed by Tukey (1949) and Rice (1945 and 1954) points are first read from the record at equal increments of time, Then the autocor- relation function of the data sample is obtained by evaluating the integral [um -ae+ ode for discrete values of time lag, 7. The raw point spec- trum is then obtained by taking the Fourier cosine transform of the autocorrelation function. Some Spiuo 4 ei da q F FREQUENCY U=27/7 fo] SPECTRUM SCALE OF TIME OR DISTANCE th) COMPONENT wavES Fig. 8 Typicel variance spectrum of waves, showing approximotion by a finite sum of components 14 PRINCIPLES OF NAVAL ARCHITECTURE [—— 100 eo 29 w =27r (sec Fig. 9 Typical sea spectra, winds from 24 to 47 knois (Moskowitr, et al, 1962) “smoothing” of the raw spectrum is desirable to im- prove the accuracy of the estimate, involving one of several smoothing functions. Finally, the theory pro- vides a means of evaluating the accuracy, that is, de- fining the confidence bands of the spectral estimates, taking account of the sampling interval 3t, the number of data points in the sample, and the number of lags. (The procedure is summarized by Korvin-Kroukovsky (1961), and discussed in detail by Bendat and Piersol 97). The foregoing operations can be readily carried ouL on a digital computer. However, in recent years, it has been found to be more expeditious to employ standard Fast Fourier programs, which also provide superior resolution (Bendat and Piersol, 1971). The effects of using different analysis methods on the same data are considered by Donelan and Pierson (1983). Many ex- amples of point spectra have been derived from ocean wave records. Several of these are shown in Fig. 9. It should be noted that some authors prefer to use a spectrum form hased on wave period rather than frequency, since it is more consistent with wave ob- servations and when plotted gives more emphasis to the important low frequencies and less to the less important high frequencies. It has been shown in Section 2.2 that energy per unit surface area in a simple harmonic wave is pro- portional to the square of the amplitude, or, more spe- cifically, a pgé* (21) Eguations (34) and (35) show that the variance of the wave components within a band of frequencies, 3, is UM) = So) do (88) which differs only by a factor of pg from the unit energy of Equation (21). Hence, the spectrum S(c), which describes the allocation of the variance ofa wave system among components can also be considered an allocation of Energy /pg. For this reason, it is some- times called, somewhat loosely, the energy spectrum. Note that if the sea were unidirectional, or long- crested, the point spectrum, together with the direc- tion, would be a complete statístical definition of the seaway, assuming it to be a Gaussian random process, with zero mean. This condition is sometimes approxi- mated in nature when the predominant waves are from a síngle distant storm. Although the variance E, obtained from a point spee- trum is a good measure of the severity of any sea, it will be shown that the seaway can be more completely characterized by considering the component wave di- rections by means of a directional spectrum. Coming now to this more general three-dimensional case, a single wave train is described by Equation (24). The general equation for the total wave system of com- ponents moving in different directions, x, is then tgp O) = BD E, cos [kl cos p, Unit Energy = + ysing)— ot + e) (39) In a manner similar to the case of the point spectrum, the wave elevation may be considered at a point (x = 0; 4 = 0), but component wave direction, u, must still be accounted for. Hence, “U)= 35 T,cos(-ot + e) (40) and UM) =E=45DE, e pão =[[ So, pl dudo (41) b where the variance E, as previously noted, is an im- portant statistical parameter, and the components are defined by both frequency, «, and direction, q, with à and ; referring to specific values of « and q, respec- tively, and the directional spectrum S(c, gu) defines the allocation by frequency and direction of the variances of the components of the wave system. Each of the infinite number of wave components is assumed to have a definite frequency and direction, with random phase angle. The component amplitudes are defined for the incremental areas, 38, in the limit as 8« and ôg > 0, when