Resolução de Exercícios sobre Transformada de Fourier, Exercícios de Comunicação

Baixe Resolução de Exercícios sobre Transformada de Fourier e outras Exercícios em PDF para Comunicação, somente na Docsity!

Exercícios Resolvidos

Séries e Transformada de Fourier

1. Mostre que X (t) ←→ 2 πx(−ω).

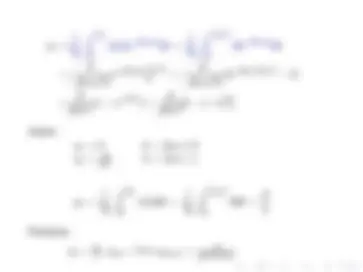
Esta transformada é conhecida como propriedade da dualidade.

Sabendo que a transformada inversa de Fourier é dada por: 1 2 π

−∞

X (ω)ejωt^ d ω = x(t)

∫ (^) ∞

−∞

X (ω)ejωt^ d ω = 2 πx(t)

Se trocarmos t por −t

∫ (^) ∞

−∞

X (ω)e−jωt^ d ω = 2 πx(−t)

Se trocarmos agora t por ω

∫ (^) ∞

−∞

X (t)e−jωt^ dt = 2 πx(−ω)

2. Mostre que

x(t). cos(ω 0 t) ←→ 1 2

X (ω − ω 0 ) + 1 2

X (ω + ω 0 )

Que é conhecida como Teorema da Modulação.

Solução: Lembrando que:

cos(ω 0 t) =

[

ejω^0 t^ + e−jω^0 t

]

Teremos:

x(t). cos(ω 0 t) = 1 2

x(t)ejω^0 t^ + 1 2

x(t)e−jω^0 t

Finalmente, aplicando a propriedade do deslocamento em frequência: ejω^0 t^ x(t) ←→ X (ω − ω 0 )

x(t). cos(ω 0 t) ←→ 1 2

X (ω − ω 0 ) + 1 2

X (ω + ω 0 )

3. Determine a transformada de Fourier do sinal

x(t) = e−|a|t^ a > 0 Solução: O sinal x(t) pode ser reescrito como:

x(t) = e−|a|t^ =

e−at^ (t > 0 ) eat^ (t < 0 )

Logo, aplicando na denição:

X (ω) =

−∞

eat^ e−jωt^ dt +

0

e−at^ e−jωt^ dt

−∞

e(a−jω)t^ dt +

0

e−(a+jω)t^ dt

E nalmente resolvendo a integral:

X (ω) = 1 a − jω

a + jω

4.Determine a transformada de Fourier dos seguintes sinais, usando apenas as propriedades.

a) x(t) = ejω^0 t^ ; b) x(t) = e−jω^0 t^ ; c) x(t) = cos(ω 0 t)

Solução: a)

Lembrando que: 1 ←→ 2 πδ(ω)

E aplicando a propriedade do deslocamento em frequência:

ejω^0 t^ x(t) ←→ X (ω − ω 0 )

Chegamos facilmente a transformada:

ejω^0 t^ ←→ 2 πδ(ω − ω 0 )

Solução: b)

Usando as mesmas propriedades da letra a), e lembrando que:

e−jω^0 t^ x(t) ←→ X (ω + ω 0 )

Chegamos a transformada:

e−jω^0 t^ ←→ 2 πδ(ω + ω 0 )

5. Determine a representação em série de Fourier exponencial complexa do sinal:

x(t) = cos( 4 t) + sen( 6 t)

Solução: Sabendo que, para garantir a periodicidade o seguinte

critério deve ser garantido:

x(t + T ) = x 1 (t + T 1 ) + x 2 (t + T 2 ) = x 1 (t + mT 1 ) + x 2 (t + kT 2 ).

Isto implica que:

mT 1 = kT 2 = T (∗)

ou

T 1 T 2

= k m

= Racional

T 1

T 2 =^

k m =^ Racional

Pode-se observar que:

ω 1 = 4 =

2 π T 1 →^ T^1 =^

π 2 ω 2 = 6 = 2 π T 2

→ T 2 = π 3

Assim, podemos observar que, usando a relação (*), teremos que:

m π 2

= k π 3

→ m = 2 e k = 3 ⇒ T = π

Conhecendo o período do sinal, podemos determinar a frequência angular:

ω 0 =

2 π T =^

2 π π =^2

6. Considere a onda quadrada periódica x(t) mostrada abaixo. determine a série de Fourier de x(t)

Solução:

Seja

x(t) =

∑^ ∞

k=−∞

ck ejkω^0 t^ ω 0 = 2 π T 0

Usando a expressão para o cálculo dos coecientes

ck =

T 0

∫ T 0

0

x(t)e−jkω^0 t^ dt = (^) T^1 0

∫ T 0 / 2

0

Ae−jkω^0 t^ dt

ck =

T 0

∫ T 0

0

x(t)e−jkω^0 t^ dt =

T 0

∫ T 0 / 2

0

Ae−jkω^0 t^ dt

= A −jkω 0 T 0

e−jkω^0 t^ |T 0 0 /^2 = A −jkω 0 T 0

(e−jkω^0 T^0 /^2 − 1 )

= (^) jkA 2 π ( 1 − e−jkπ) = (^) jkA 2 π [ 1 − (− 1 )k^ ]

Assim: ck = 0 k = 2 m 6 = 0 ck = (^) jkAπ k = 2 m + 1

c 0 = 1 T 0

∫ T 0

0

x(t)dt = 1 T 0

∫ T 0 / 2

0

Adt = A 2

Portanto,

c 0 = A 2 , c 2 m = 0 e c 2 m+ 1 = (^) j( 2 mA+ 1 )π