















































































Estude fácil! Tem muito documento disponível na Docsity

Ganhe pontos ajudando outros esrudantes ou compre um plano Premium


Prepare-se para as provas
Estude fácil! Tem muito documento disponível na Docsity
Prepare-se para as provas com trabalhos de outros alunos como você, aqui na Docsity
Os melhores documentos à venda: Trabalhos de alunos formados
Prepare-se com as videoaulas e exercícios resolvidos criados a partir da grade da sua Universidade
Responda perguntas de provas passadas e avalie sua preparação.

Ganhe pontos para baixar
Ganhe pontos ajudando outros esrudantes ou compre um plano Premium
Comunidade
Peça ajuda à comunidade e tire suas dúvidas relacionadas ao estudo
Descubra as melhores universidades em seu país de acordo com os usuários da Docsity
Guias grátis
Baixe gratuitamente nossos guias de estudo, métodos para diminuir a ansiedade, dicas de TCC preparadas pelos professores da Docsity
Apostila de Concreto Armado - volume 3: uma revisão geral, diferenças e objetivo do seu uso
Tipologia: Notas de estudo

Oferta por tempo limitado
Compartilhado em 30/10/2014
3.5
(2)2 documentos
1 / 93

Esta página não é visível na pré-visualização
Não perca as partes importantes!























































































Em oferta
- 2014/2 -
ANEXOS – Ábacos adimensionais para dimensionamento na flexão composta reta 69
1.2. Coeficientes de ponderação
A NBR 6118, em seus itens 11.6.1 e 12.2, define os valores característicos para as grandezas envolvidas nas verificações dos estados limites (ou seja, as ações e as resistências).
1.2.1 Valores característicos para as resistências Os valores característicos fk a serem considerados para as resistências de um material são definidos como os valores que têm uma probabilidade de apenas 5% de não serem atingidos em um determinado lote do material. Admite-se uma distribuição normal para estas resistências.
fck = fcm - 1,65 sc fk = fm - 1,65 s fyk = fym - 1,65 sy
n 1
(f f ) s
n
i 1
2 i m
A NBR 6118, em seu item 8.2.1, define classes de resistência em MPa para o concreto. Para superestruturas de concreto armado, o concreto deve ser no mínimo de classe C20 ( fck = 20 MPa). Para estruturas de fundações e em obras provisórias, o concreto pode ser de classe C15 ( fck = 15 MPa). A NBR6118, em sua versão 2014, é aplicável para concretos de classe até C90. A resistência característica do aço à tração, fyk (ou à compressão, fyck ) é definida em função da tensão mínima de escoamento, real ou convencional, fixada como sendo a tensão correspondente à deformação específica permanente de 0,2%, determinada de acordo com a NBR 6152. Os aços para concreto armado são classificados pela NBR 7480, de acordo com o valor característico da sua resistência de escoamento, nas categorias CA-25, CA-50 e CA-60.
1.2.2 Valores de cálculo para as resistências As resistências de cálculo são estabelecidas pela NBR 6118, no seu item 12.3, a partir dos respectivos valores característicos e dos coeficientes de ponderação das resistências. Estes coeficientes levam em conta a variabilidade da resistência dos materiais envolvidos, as diferenças entre resistências medidas em corpos de provas e nas estruturas, desvios ocorridos na construção das estruturas e aproximações feitas no projeto, do ponto de vista das resistências. Para verificações estruturais realizadas com concreto de idade igual ou superior a 28 dias, as expressões abaixo se aplicam.
1.2.3 Valores característicos e valores representativos para as ações e solicitações Os valores característicos a serem considerados para as ações Fk são definidos nas diversas Normas Brasileiras pertinentes, em função de uma probabilidade de estes valores serem ultrapassados durante a vida útil da construção. Para as cargas permanentes, a NBR 8681 define os valores característicos como os seus próprios valores médios. Para as cargas acidentais, os valores característicos são aqueles que têm de 25% a 35% de probabilidade de serem ultrapassados no sentido desfavorável em 50 anos, o que corresponde a períodos de recorrência de, respectivamente 174 e 117 anos. Não se dispondo de dados estatísticos
suficientes, como é o caso em geral para as ações variáveis, os valores característicos a serem considerados são os valores nominais fixados pelas Normas Brasileiras específicas, para cada tipo de carregamento. Para vento e sismo, as probabilidades de ultrapassagem em 50 anos são fixadas nas Normas NBR 6123 e NBR 15421 em 63% e 10%, respectivamente, o que corresponde a períodos de recorrência de 50 e 475 anos.
1.2.4 Valores de cálculo para as ações e solicitações A NBR 6118, no seu item 11.7, define valores de cálculo para as ações, por meio de
atuação das ações, desvios gerados na construção não explicitamente considerados no cálculo e as aproximações feitas no projeto do ponto de vista das solicitações. Os valores de cálculo das ações são genericamente, os valores das ações representativas vezes os coeficientes de majoração:
Nos casos em que os pilares e pilares-parede tenham sua menor dimensão entre 14 e 19 cm,
menor dimensão da seção transversal do pilar em cm, de acordo com o item 13.2.3 da NBR 6118. Este coeficiente adicional é justificado pela maior probabilidade de falhas de construção em peças esbeltas e da maior importância relativa dos desvios construtivos, por exemplo, nos cobrimentos. Pilares de
1.2.5 Ponderação das ações nos estados limites últimos (ações variáveis de só um tipo): Fd = 1,4 Fgk + 1,4 F (^) qk + 1,2 F k. (condições normais, quando as ações são desfavoráveis) (ou 1,0 Fgk , 0,0 F (^) qk , 0,0 F k. ) (condições normais ou de construção, quando as ações são favoráveis) Fd = 1,3 Fgk + 1,2 F (^) qk + 1,2 F k. (condições de construção, quando as ações são desfavoráveis)
( Fgk - ação permanente característica, Fqk - ação variável característica, F k. - ação característica devida a deformações próprias e impostas: recalques de apoio, retração, temperatura, etc.) No caso dos efeitos da carga variável decorrerem da atuação simultânea de cargas acidentais e de vento, considera-se a baixa probabilidade dos dois carregamentos atingirem simultaneamente o seu valor máximo. Neste caso, se considera a soma dos efeitos máximos de um carregamento, com o outro reduzido por um fator ψ 0 (aplica-se uma redução também para os efeitos de temperatura):
Fd g.Fgkq.(Fq 1 k 0 j.Fqjk)q . 0 .Fqk
As seguintes combinações devem ser verificadas (Tabela 11.3 da NBR 6118):
1.2.5.3 Exemplo 3: Seja um pilar de concreto simples, de área igual a Ap em que a força normal de compressão é: Np = Ng + Nq A tensão de compressão atuante no concreto é de:
A tensão de rutura em um dado corpo de prova padronizado do concreto do pilar é de:
Onde Ne é a força de compressão que rompe o corpo de prova e Ae é a área do corpo de prova. A verificação de segurança ( é ilustrada na figura abaixo:
1.2.6 Ponderação das ações nos estados limites de serviço: Pode ser sempre conservadoramente considerado:
cargas acidentais, de vento e de temperatura podem ser considerados, conforme item 11.7.2 da NBR
1.3 Características dos aços Para o cálculo nos estados limites últimos, considera-se o diagrama tensão-deformação bilinear genérico para os aços, definido pela NBR 6118 em seu item 8.3.6. O patamar de escoamento é bem definido e sem acréscimo de tensões após a deformação de escoamento. A aplicação dos critérios de dimensionamento que serão a seguir detalhados leva ao diagrama tensão-deformação de projeto dado a seguir.
Considera-se, para todos os tipos de aço, Es = 210 000 MPa = 21 000 kN/cm^2 = 21. 10^7 kN/m^2. No caso, por exemplo, do aço CA-50: f yd = f ycd = 50/1,15 = 43,48 kN/cm^2 yd = f yd / Es = 43,48/21000 = 0,002070 = 2,070 0 / 00 Os valores de f yd e yd para os três tipos de aço são fornecidos na tabela abaixo:
As bitolas da tabela a seguir são as das barras normalizadas pela NBR 7480 (“Barras e fios destinados a armaduras para concreto armado”). É fornecida também a área em cm^2 de cada bitola.
para concretos de classes até C50: c2 = 2,0^0 / 00 cu = 3,5^0 / 00 para concretos de classes de C50 até C90: c2 = 2,0^0 / 00 + 0,085^0 / 00 .( fck - 50)0, cu = 2,6^0 / 00 + 35^0 / 00 .[(90 - fck )/100]^4
Estimativa para o módulo de elasticidade inicial (item 8.2.8 da Norma), a ser utilizado nas análises globais de uma estrutura, quando não forem realizados ensaios para a determinação deste parâmetro (unidade, MPa):
1 / 3 ck (^1) , 25 10
^^ f , para f ck de 55 MPa a 90 MPa.
O parâmetro E depende da rocha matriz da brita empregada:
Estimativa para o módulo de elasticidade secante a ser utilizado nas análises locais e seccionais de uma estrutura:
Ecs = i. Eci
f^ ck ≤ 1,
Coeficiente de Poisson = 0,2 (item 8.2.9 da Norma) Coeficiente de dilatação térmica = 10-5^ /^0 C (item 8.2.3 da Norma)
1.5 Hipóteses básicas no dimensionamento à flexão simples no estado limite último.
O dimensionamento de uma peça composta de um material homogêneo, com comportamento suposto como elástico linear, pode ser efetuado pelo método das tensões admissíveis. Por exemplo, para uma viga de seção retangular (b x h), submetida à flexão simples (momento fletor igual a M), as tensões máximas de compressão e de tração são ambas iguais a = 6M/bh^2 , devendo esta tensão ser comparada com um valor de tensão admissível definido para este material. Para o dimensionamento do concreto armado, o problema é bem mais complexo, devendo ser considerados os diagramas não-lineares tensão-deformação já definidos para o concreto e para o aço, e as hipóteses básicas a seguir enunciadas.
d
cu
%
c x
0,85 fcd
y=λx
αc fcd ou 0,9 αc fcd
^ (Domínio 3) s
Deformação plástica excessiva: reta a : tração uniforme. domínio 1 : tração não uniforme, sem compressão. domínio 2 : flexão simples ou composta, sem ruptura à compressão do concreto, aço a 10^0 / 00 Ruptura: domínio 3 : flexão simples (seção sub-armada) ou composta, com ruptura à compressão do concreto, e com escoamento do aço. domínio 4 : flexão simples (seção super-armada) ou composta, com ruptura à compressão do concreto, e com aço tracionado sem escoamento. domínio 4a : flexão composta com armaduras comprimidas. domínio5 : compressão não uniforme, sem tração. reta b : compressão uniforme.
2.1 Dimensionamento na flexão composta reta – fck ≤ 50 MPa
As diversas possibilidades de dimensionamento e verificação das seções de concreto armado na flexão composta reta se realizam quando os diversos domínios de deformações específicas no estado limite último são percorridos: tração simples, flexão composta com tração, flexão simples, flexão composta com compressão e compressão simples. Durante este desenvolvimento, a profundidade da linha neutra assume os valores: Domínio 1: de - ∞ a 0 Domínio 2: de 0 a 0,259 d Domínios 3 e 4: de 0,259 d a d Domínio 4a: de d a h Domínio 5: de h a + ∞ A retangularização do diagrama tensão-deformação do concreto só será considerada para concretos com fck ≤ 50 MPa. Para concretos com resistência superior a esta, a retangularização leva a resultados muito imprecisos, obrigando à consideração dos diagramas tensão-deformação reais. São inicialmente definidas as notações a serem seguidas, através das figuras abaixo:
s c
i s si d
t d'
1
d
( (^) s c).(ti d') si s
d
( (^) c).(ti d') si
De acordo com o diagrama tensão-deformação definido no item 2.3, as tensões na armadura serão:
yd si yd si
si si (^) .f ^
A força Fsi (de tração) na armadura genérica i é dada por: Fi = Asi. σsi O equilíbrio entre forças externas aplicadas e forças internas leva aos esforços externos equilibrantes:
Nd (^) Fi ; d (^) d Fi.ti
h M N. 2 Nas peças submetidas à tração pura ou composta com flexão é necessária a verificação à fissuração, de acordo com o item 17.3.3, da NBR 6118. A NBR 6118 (versão 2007), em seu item 17.3.3, fornece uma alternativa ao cálculo analítico da abertura esperada de fissuras. Para os diversos diâmetros das barras, é definida uma tensão máxima nas mesmas, em condições de serviço, e um espaçamento máximo das armaduras. Desta forma, esperam- se aberturas máximas de fissuras da ordem de 0,3 mm. É atendido desta forma o estado limite de fissuração. Estes valores são definidos na tabela a seguir.
Diâmetro da armadura (Ф)
Tensão máxima em serviço (σs), em MPa
Espaçamento máximo (smax), em cm
Acréscimo da armadura (CA-50) 10 360 5 1, 12,5 320 10 1, 16 280 15 1, 20 240 20 1, 25 200 25 1, 32 160 30 1, 2.1.2 Equações para o Domínio 2 O Domínio 2 corresponde a diversas condições de equilíbrio em que a parte superior da seção está comprimida e as armaduras superiores encontram-se tracionadas ou comprimidas. O estado limite
corresponde a diversas situações de flexão composta com tração, flexão simples e flexão composta com compressão.
O Domínio 2 é definido pelas seguintes condições de deformação específica:
Profundidade da linha neutra x :
c s 1
x d. c
d
x k (^) x ,max max
Para o cálculo das deformações específicas no nível da armadura genérica i , vale a expressão
forças nas armaduras também são determinadas com as expressões do Domínio 1. A força de compressão Fc , resultante das tensões de compressão atuantes no concreto, é determinada com a expressão a seguir, devendo Fc ser tomado com o sinal negativo (compressão):
Fc 0 , 85 .fcd.b. 0 , 8 .x Para o equilíbrio de momentos é necessário definir a distância do ponto de aplicação da força Fc à face inferior da seção:
tc h 0 , 4 .x O equilíbrio entre forças externas aplicadas e forças internas leva aos esforços externos equilibrantes:
Nd Fc Fi ;
F.t F.t 0 2
h M (^) d Nd. c c i i d (^) d Fc.tc Fi.ti h M N. 2 2.1.3 Equações para o Domínio 3 O Domínio 3 corresponde a diversas condições de equilíbrio em que a parte superior da seção está comprimida e as armaduras encontram-se tracionadas ou comprimidas. O estado limite se caracteriza pelo esgotamento da capacidade de encurtamento do concreto, suposto com sua máxima
simples e flexão composta com compressão. O Domínio 3 é definido pelas seguintes condições de deformação específica:
O cálculo da profundidade de linha neutra é igual ao do Domínio 2, sendo que no Domínio 3,
d
x k (^) x ,max max
As expressões do Domínio 2 para o cálculo das deformações específicas no nível da armadura genérica i , de tensões e forças nas armaduras, da força de compressão no concreto e de equilíbrio entre forças externas aplicadas e forças internas permanecem válidas.
2.1.4 Equações para os Domínios 4 e 4a O Domínio 4 corresponde a diversas condições de equilíbrio em que a parte superior da seção está comprimida e as armaduras encontram-se tracionadas ou comprimidas. O estado limite se caracteriza pelo esgotamento da capacidade de encurtamento do concreto, suposto com sua máxima
Substituindo 7 14
c
c .
x h.
, vem:
( 3 .h. )/( 7 14 )
t ( 3 .h. )/( 7 14 ) h . c c
i c c si c
c
i c i c c si c .h.
.t. .t .h. .h. .h .
3
.h
.t (^) i.c .ti .h.c .h si (^) 3
As expressões do Domínio 3 para tensões e forças nas armaduras, da força de compressão no concreto e de equilíbrio entre forças externas aplicadas e forças internas permanecem válidas.
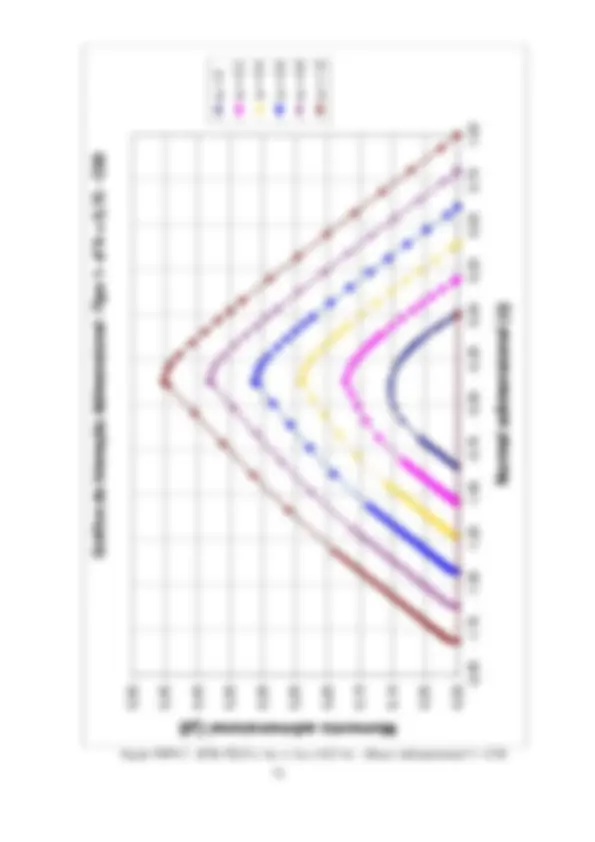
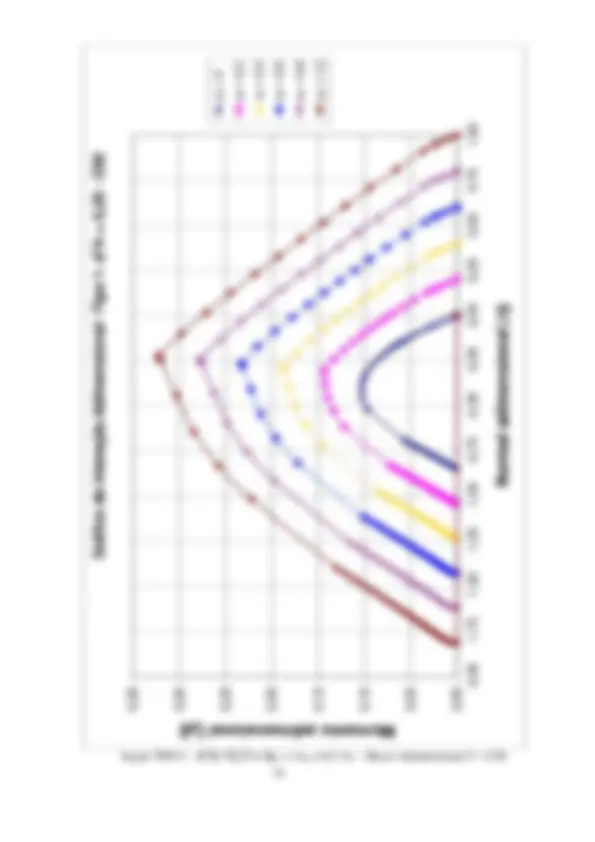
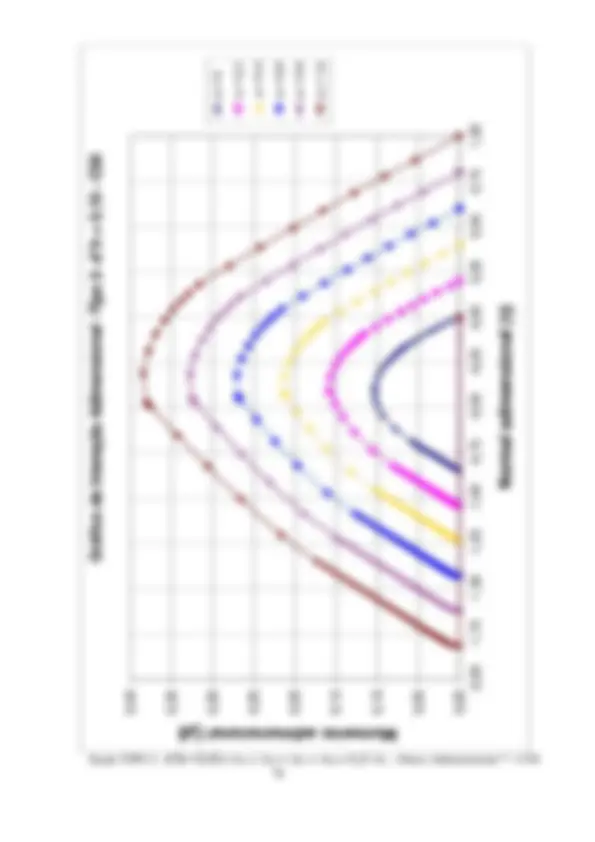
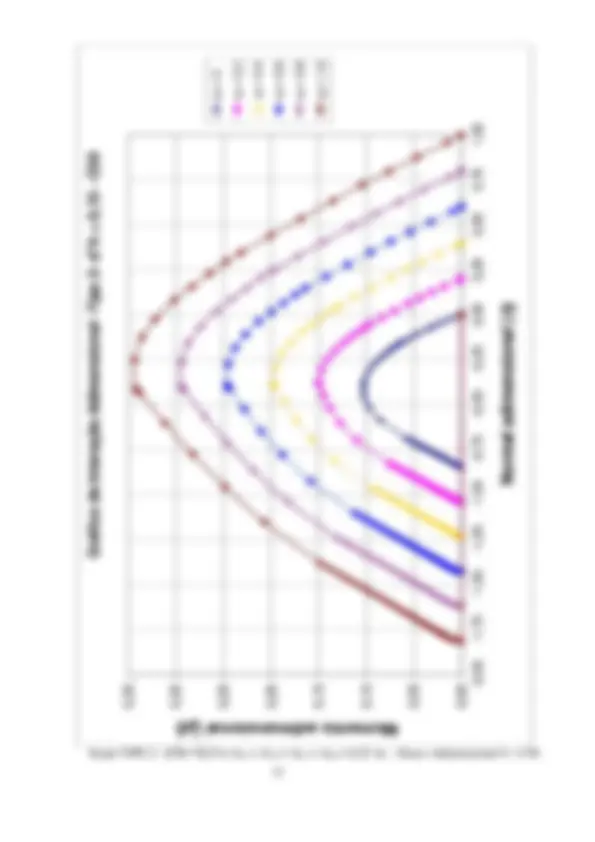
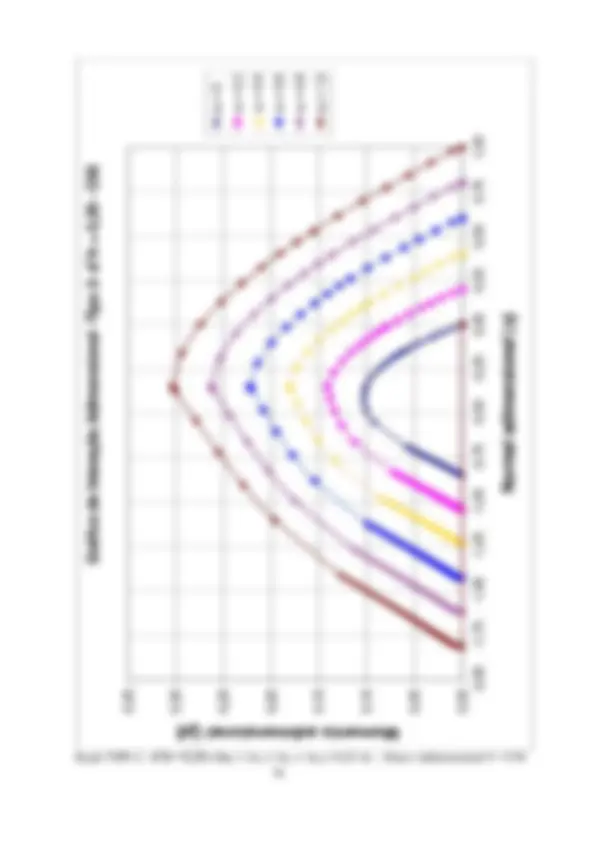
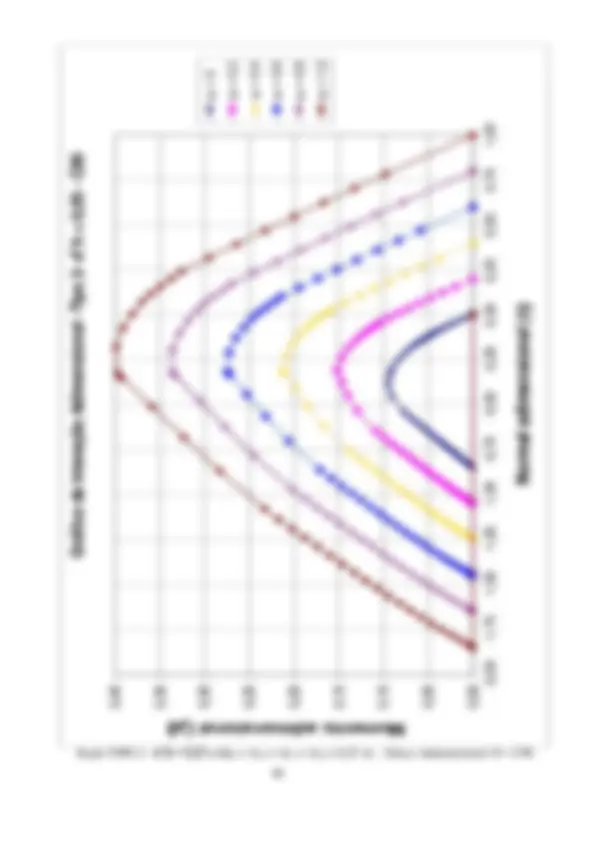
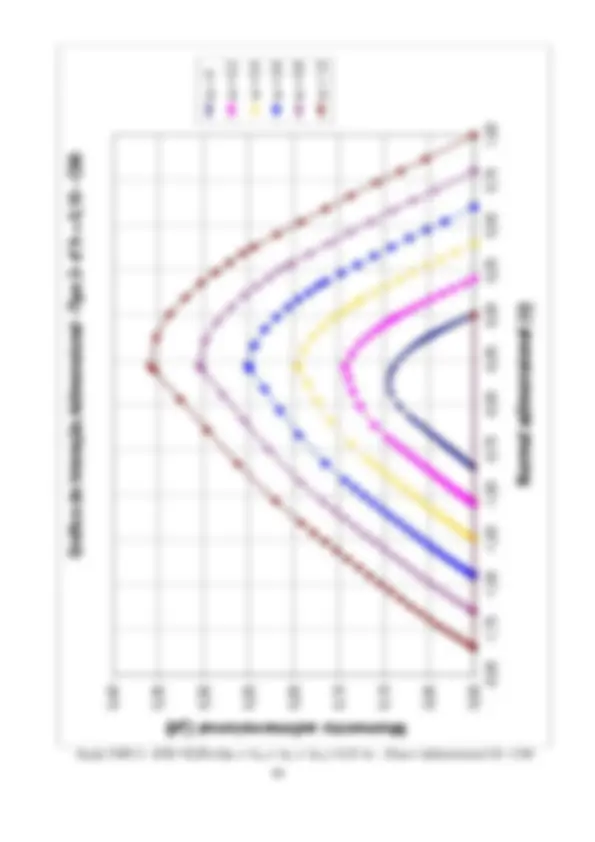
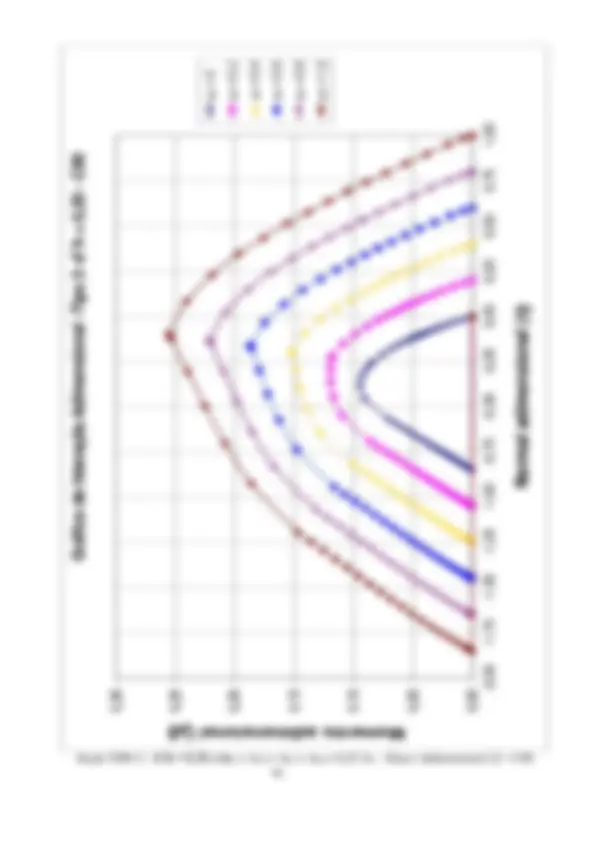
2.2 Planilhas de dimensionamento. Ábacos de interação ( fck ≤ 50 MPa)
A formulação apresentada no item 2.1 é sistematizada através de planilhas EXCEL. Estas planilhas têm um formato que permitem a verificação de uma seção retangular qualquer submetida à flexão composta reta. Também com estas planilhas serão geradas tabelas adimensionais, que expressas graficamente, permitirão o dimensionamento através de ábacos de interação. Estas planilhas consideram a retangularização do diagrama tensão-deformação do concreto, considerada como adequada para concretos com fck ≤ 50 MPa.
2.2.1 Exemplo de dimensionamento. Duas camadas, armadura simétrica. É apresentada, nas páginas seguintes, a planilha correspondente ao primeiro exemplo (arquivo “FlexãoComposta-Dimensionamento ou FlexãoComposta-Dimensionamento-Bitolas”).
A planilha EXCEL da página seguinte fornece os seguintes dados e resultados, sendo cada linha correspondente às diversas configurações deformadas, nos diversos Domínios da NBR 6118: x(m) – profundidade da linha neutra. No Domínio 5, foi limitada, para viabilizar o cálculo automático da compressão no concreto, a h/0,8.
concreto e das armaduras As1 e As. s1 (kN/cm^2 ) e s1 (kN/cm^2 ) – tensões nas armaduras As1 e As2. pares de valores resistentes Nd , Md para a armadura fornecida e para As = 0 e valores atuantes na seção. Na figura em página posterior, estes valores de Nd e Md são plotados em curvas de interação. Observar que, com a armadura adotada, os valores atuantes estão na região segura (interna) do ábaco. É traçada uma linha reta, unindo dois pares de valores com a mesma posição de linha neutra, para a armadura fornecida e para As = 0, passando próximo ao ponto correspondente ao par de esforços atuante. Observar, que nesta reta, os acréscimos nos pares de esforços resistentes são proporcionais à armadura adotada, permitindo assim uma interpolação (ou extrapolação). A adoção deste procedimento no exemplo leva às armaduras As1 = As2 = 3cm^2 , o que é uma excelente aproximação para a solução exata. Resolvendo pelos ábacos de interação adimensionais, a serem apresentados no item 2.2.2, considerando o ábaco Adimensional 3:
0 , 117 0 , 6. 0 , 3. 20000 / 1 , 4
b.h .f
b.h.f
2 cb
2
d cd
d^
Com este par de valores, encontra-se, por interpolação, no Ábaco, ω = 0,1.
Como: s^2 cd
s yd 5 , 9 cm 50 / 1 , 15
b.h.f
A .f ,
o que confirma que a armadura acima avaliada.