Baixe MODELO DE CÁLCULO DE SAPATA ISOLADA SUBMETIDA À CARGA CENTRADA e outras Notas de aula em PDF para Engenharia Civil, somente na Docsity!
MODELO DE CÁLCULO DE SAPATA ISOLADA SUBMETIDA À
CARGA CENTRADA
1) O caso mais usual em edifícios.
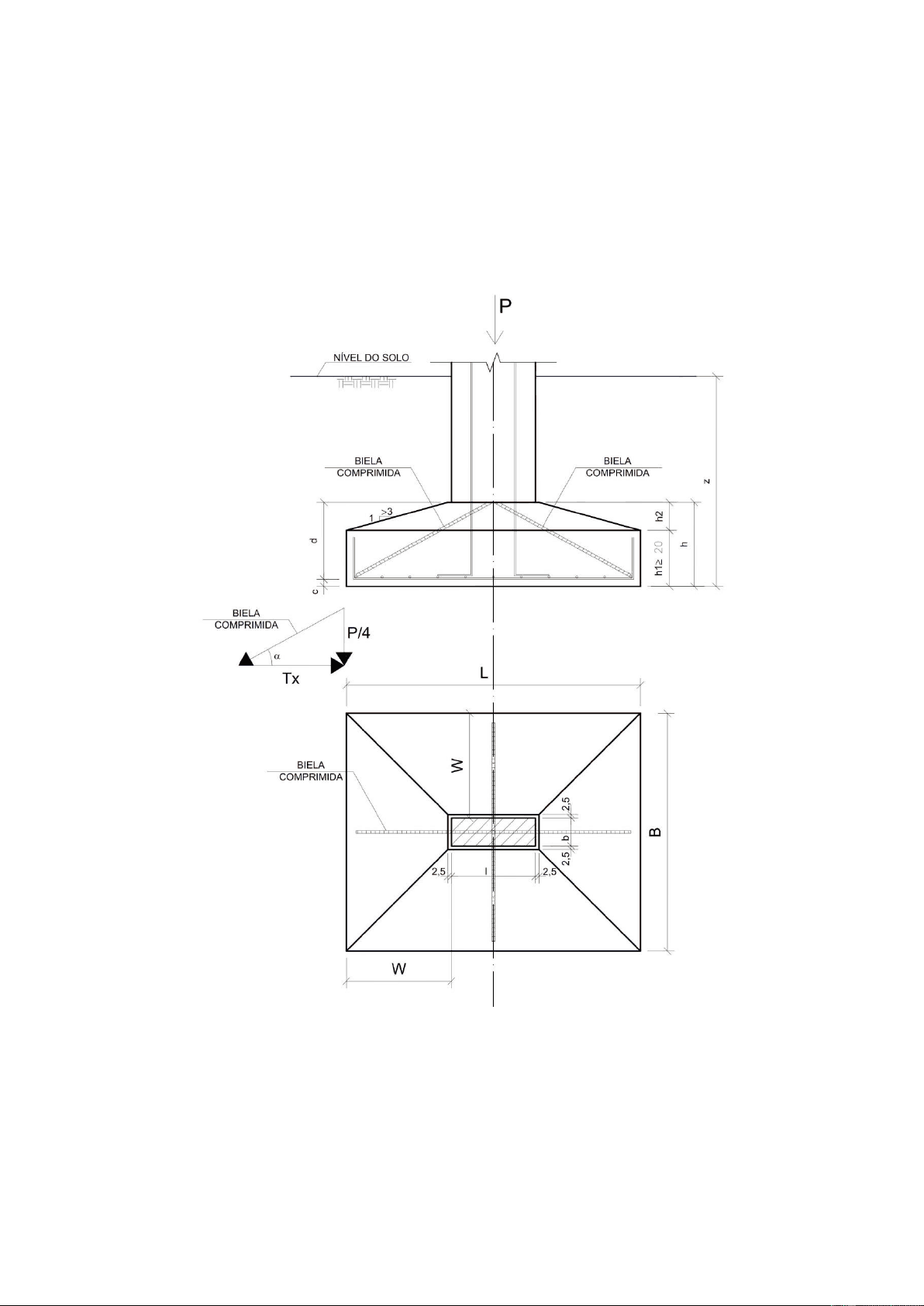
Considere o desenho esquemático da sapata:
O dimensionamento de sapatas é um processo interativo, visto que a tensão aplicada ao solo é fruto da soma da carga aplicada ao pilarete, do peso próprio da sapata e do peso de solo sobre a sapata - reaterro – dividido pela área adotada. O modelo proposto admite que o peso próprio e o reaterro, inicialmente, sejam uma parcela da carga aplicada, para,
posteriormente, serem confirmados após o dimensionamento. Tal parcela
varia entre 15% e 25% da carga aplicada normalmente.
L.B =
P(1+k) σadm
Recomenda-se que:
L B ≤ 2,
Posteriormente a esta etapa, verifica-se a tensão final aplicada ao solo.
σa =
P+ Pf+ Ps L.B
Recomenda-se a seguinte relação de trabalho:
σa σadm^ ≤ 1,
Caso esta relação não seja atendida, a sapata deverá ser
redimensionada.
A altura da sapata é determinada de forma que a sapata seja classificada
como rígida, sendo possível o emprego do método das bielas para o
dimensionamento. Deve-se levar em conta também o fato de que a
sapata trabalha a punção, portanto deve apresentar altura suficiente para
absorver tais solicitações.
Neste modelo será usado o método proposto por Caquot para se
proceder a um pré-dimensionamento da altura útil, mas, posteriormente,
a sapata será verificada a punção conforme as recomendações da
ABNT: NBR 6118:2003.
Para que a sapata seja considerada rígida, deve possuir altura de acordo
com a equação abaixo, conforme dispõe o item 22.4.1 da NBR 618:2003:
Por analogia, na direção y:
Ty=
P (B − b) 8d
Considerando:
γs = 1,15 e γ = 1,
γs. γ = 1,15 × 1,40 = 1,
Portanto, a armadura na direção x pode ser determinada pela expressão:
Asx =
1,61 × Tx fyk → armadura paralela ao lado L
E, por analogia:
Asy =
1,61 × Ty fyk → armadura paralela ao lado B
3) Verificação da punção conforme item 19.5.3.
δsd≤ δrdz = 0,27. αy. fcd
Onde:
αy = 1 -
fck 250 , com o fck em MPa
δsd =
Fsd μ. d (item 19.5.2.1 da NBR 6118: 2003)
Como: Fsd = 1,4 P
δsd =
1,4 P
μo. d
Onde: d é a altura útil da sapata e μo é o perímetro de c (contorno do pilarete),
dado por:
μo = 2b + 2l ∴ μo = 2(b + l)
Convém observar que no caso de sapata rígida o cisalhamento ocorre por compressão diagonal e não apresenta ruptura por tração diagonal. Isso porque a sapata rígida fica inteiramente dentro do cone hipotético de punção, não havendo, portanto, possibilidade física de punção.
4) Observações importantes A norma brasileira considera como rígida a sapata que apresenta altura;
h ≥ {
L − l 3 B − b 3
No entanto, alguns trabalhos apresentados na literatura definem como rígidas
as sapatas que apresentam a seguinte altura útil:
d ≥ {
L − l 4 B − b 4 O dimensionamento econômico será aquele que conduz a momentos aproximadamente iguais nas duas direções. Nestas condições:
B = b + 2w
L = l + 2w
EXERCÍCIO
Dimensionar a sapata de forma econômica para receber um pilar de 20 x 60 cm
e carga de 1000 kN, sendo fornecida a sondagem ( Standard Penetration Test )
conforme a NBR 6484. Considerar fck = 25 MPa e aço CA-50.
Solução:
- Determinação da pressão admissível do solo e escolha da cota de assentamento da sapata.
Observando o relatório de sondagem é possível determinar a cota de assentamento das fundações. Neste caso, será adotada a profundidade de 1,50 m, a qual atende aos seguintes quesitos básicos:
1.1. Encontra-se acima do nível d’água. 1.2. Não há acréscimo significativo do número de golpes nas camadas inferiores. 1.3. O número de golpes das camadas inferiores encontra-se entre 7 e 25 (região de estudo). 1.4. A profundidade mínima recomendada pela NBR 6122 é de 1,50 m, portanto a mais econômica, requerendo menos escavação.
Pressão admissível do solo – baseado no modelo proposto por Terzaghi e Peck (1948).
Inicialmente, pré-dimensione o elemento considerando apenas o número de
golpes na camada de assentamento e desconsiderando o peso próprio da
fundação e o peso de solo sobre a fundação. O elemento é suposto quadrado.
NSPT 0 = 11
σadm0 =
NSPT 0
50 ∴ σadm0^ = 0,22 MPa
B 0 = √
P
σadm
∴ B 0 = 2,13 m
z = 2,0. B 0 = 2,0. 2,13 = 4,26 m
C. A. ≤ z ≤ C. A. +2,0. B 0 1,5 m ≤ z ≤ 1,5 + 4, 1,50 m ≤ z ≤ 5,76 m
NSPT =
4 ∴ NSPT = 16
σadm =
NSPT
50 ∴ σadm^ = 0,32 MPa
Pressão admissível do solo – baseado na tabela 4 da NBR 6122
- Solo abaixo da cota de assentamento da sapata – argila rija, classe 11, portanto: σ 0 = 0,2 MPa
Como se trata de solo compreendido entre as classes 10 e 15 – argiloso – e
que o corpo de fundação é menor que 10 m², conforme item 6.2.2.7 da NBR
6122 σadm = σ 0 , logo:
σadm = 0,2 MPa
Para métodos empíricos, como a referida tabela, o item 6.2.1.4 da NBR
6122/1996 recomenda que as cargas não sejam superiores a 1000 kN.
Para continuação deste exercício será adotado o primeiro método – Terzaghi e
Peck – portanto:
σadm = 0,32 MPa
Determinação da altura:
σa = 0,85. (
fck 1,96) = 0,28. 25000 ∴ σa^ = 10.842 kPa
d ≥ 1,44 √
10842 ∴ d ≥ 0,44 m
h = d + 5,0 cm
h = 0,44 + 0,05 ∴ h = 0,49 m
h ≥ {
L − l 3 =
3 = 0,52 m B − b 3 =
3 = 0,52 m
Adotando h = 0,55 m:
h 2 ≤ {
L − (l + 0,05) 6 =
6 = 0,25 m B − (b + 0,05) 6 =
6 = 0,25 m
Adotado:
Vf = (0,2. 0,60. 0,95) + (1,75. 2,15. 0,30) + {
3 [(0,25. 0,65) + (1,75. 2,15) + √0,25. 0,65. 1,75. 2,15 ]}
Vf = 1,62 m^3
Vs = (2,15. 1,75. 1,50) − 1,
Vs = 4,02 m³
Pf = Vf. γf = 1,62. 25 ∴ Pf = 40,50 kN
Ps = Vs. γs = 4,02. 18 ∴ 72,36 kN
σa =
P + Pf + Ps L. B
h 2 = 0,25 m
h 1 = 0,30 m
σa =
2,15. 1,75 ∴ σa^ = 295,78 kPA
σa σadm^ =
320 ∴^
σa σadm^ = 0,
Verificação da pressão aplicada ao solo:
σa σadm^ ≤ 1,05^ NÃO OK
Adotando k = 0,15:
L. B =
320 ∴ L. B = 3,59 m²
O dimensionamento econômico é obtido quando:
L − B = 60 − 20 L − B = 40 cm ∴ L − B = 0,40 m
Para obter as dimensões econômicas, B e L devem atender, simultaneamente,
as duas equações, portanto resolve-se o seguinte sistema de equações:
{L − B = 0,40L. B = 3,59^ II
∴ L = 0,40 + B I
Substituindo I em II:
L. B = 3, (0,40 + B ). B = 3, B^2 + 0,40. B − 3,59 = 0 Δ = 0,40^2 − (−4. 1. 3,59) ∴ Δ = 14,
𝐵′^ = −2,
Adotado: B = 1,70 m
Vs = 3,87 m³
Pf = Vf. γf = 1,49. 25 ∴ Pf = 37,25 kN
Ps = Vs. γs = 3,87. 18 ∴ 70,02 kN
σa =
P + Pf + Ps L. B
σa =
2,10. 1,70 ∴ σa^ = 310,16 kPA
σa σadm^ =
320 ∴^
σa σadm^ = 0,
Verificação da pressão aplicada ao solo:
σa σadm^ ≤ 1,05^ OK
- Dimensionamento das armaduras
Tx =
P (L − l) 8d =
- 0,45 ∴ Tx^ = 416,67 kN
Ty =
P (B − b) 8d =
- 0,45 ∴ Tx^ = 416,67 kN
Como: Tx = Ty
Asx = Asy =
1,61 T
fyk =
Asx = Asy = 13,42 cm²
Adotando a barra de 10,0 mm de diâmetro, temos:
Af =
π ϕ^2 4 =
π. 1,0^2 4 ∴ Af = 0,7854 cm
2
Número de ferros – igual nas duas direções, pois, neste caso, Asx = Asy
Nf =
As Af =^
Adotado: Nf = 14
Espaçamento entre ferros: Na direção x – armadura paralela ao lado L
Espx =
B − 2c Nfx − 1 =
17 − 1 ∴ Espx^ ≅ 10,0 cm
Na direção y – armadura paralela ao lado B
Espy =
L − 2c Nfy − 1 =
17 − 1 ∴ Espy^ ≅ 12,5 cm
- Verificação do cisalhamento – compressão diagonal
μ 0 = 2(b + l) = 2(0,2 + 0,60) ∴ μ 0 = 1,60 m
d = h − 0,05 = 0,50 − 0,05 ∴ d = 0,45 m
F = σa (L. B − l. b)
F = 310,16. [(2,10. 1,70) − (0,20. 0,60)] ∴ F = 1070,05 KN
τsd =
1,60. 0,45 ∴ τsd^ = 2,08 MPa
τRd2 = 0,27. αv. fcd
αv = 1 −
fck 250 = 1 −^
250 ∴ αv^ = 0,
τRd2 = 0,27. 0,.
1,4 ∴ τRd2^ = 6,08 MPa
τsd < τRd2 OK
Usar 17 Φ 10,00 mm nas duas direções
Relatório de Sondagem:
