Método de Gauss-Seidel para a
solução numérica de equações
lineares
Ruyano Gabriel Almeida de Resende
Prepare-se para as provas
Estude fácil! Tem muito documento disponível na Docsity
Ganhe pontos para baixar
Ganhe pontos ajudando outros esrudantes ou compre um plano Premium
Guias e Dicas
Prepare-se para as provas
Estude fácil! Tem muito documento disponível na Docsity
Encontrar documentos
Prepare-se para as provas com trabalhos de outros alunos como você, aqui na Docsity
Pesquisar documentos Store
Os melhores documentos à venda: Trabalhos de alunos formados
Videoaulas
Prepare-se com as videoaulas e exercícios resolvidos criados a partir da grade da sua Universidade
Quiz
Responda perguntas de provas passadas e avalie sua preparação.
Ganhe pontos para baixar
Ganhe pontos ajudando outros esrudantes ou compre um plano Premium
Comunidade
Pergunte à comunidade
Peça ajuda à comunidade e tire suas dúvidas relacionadas ao estudo
Ranking universidades
Descubra as melhores universidades em seu país de acordo com os usuários da Docsity
Guias grátis
Os eBooks que salvam estudantes!
Baixe gratuitamente nossos guias de estudo, métodos para diminuir a ansiedade, dicas de TCC preparadas pelos professores da Docsity
Método de Gauss-Seidel para solução numérica de equações lineares, Notas de estudo de Cálculo
O documento explica o método gauss-seidel, uma variante do método jacobi-richardson, utilizada na solução numérica de equações lineares. Ele apresenta o objetivo, o que é aproveitado, as modificações e critérios de convergência. O autor também inclui observações importantes.
O que você vai aprender
- Em que situações o método Gauss-Seidel é mais indicado para solucionar equações lineares numéricas?
- Qual é a finalidade do método Gauss-Seidel em relação ao método Jacobi-Richardson?
- Quais iterações definem o processo de Gauss-Seidel?
- Como se diferenciam as matrizes dos coeficientes em Gauss-Seidel e Jacobi-Richardson?
- Quais são os critérios de convergência do método Gauss-Seidel?
Tipologia: Notas de estudo
2022
1 / 19
Esta página não é visível na pré-visualização
Não perca as partes importantes!
Documentos relacionados
Pré-visualização parcial do texto
Baixe Método de Gauss-Seidel para solução numérica de equações lineares e outras Notas de estudo em PDF para Cálculo, somente na Docsity!
Método de Gauss-Seidel para a
solução numérica de equações
lineares
Ruyano Gabriel Almeida de Resende
O que é o método de Gauss-Seidel?
O método de Gauss-Seidel é uma modificação do método de
Jacobi-Richardson, criado com o objetivo de acelerar a
convergência, ou seja utilizar menos iterações para chegar
mais próximo à resposta.
Obs.: Apesar do objetivo ser uma conversão mais rápida em comparação ao método de Jacobi-Richardson existem exemplos onde isso não ocorre.
O que muda?
Dado o sistema: Por Jacobi-Richardson temos:
O que muda?
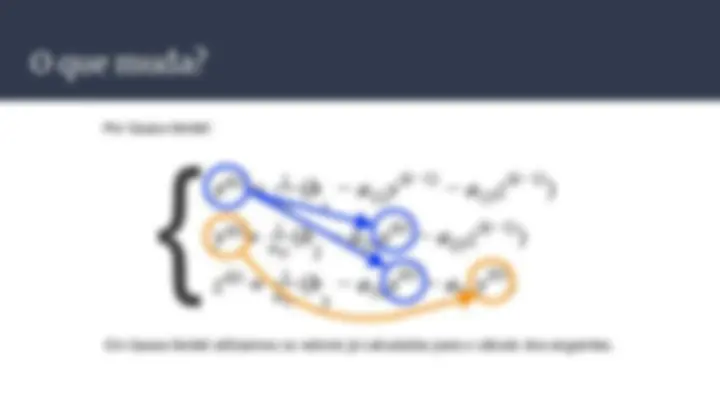
Em Gauss-Seidel utilizamos os valores já calculados para o cálculo dos seguintes.
Por Gauss-Seidel:
1 - Critério de Sassenfeld
Dado o cálculo de 𝞫i:
É satisfeito se o maior 𝞫 do sistema for menor que 1.
2 - Critério das linhas
Mesmo do aplicado em Jacobi-Richardson:
Observações:
- Pode acontecer de um sistema linear seja convergente quando aplicado Jacobi-Richardson enquanto que se aplicado em Gauss-Seidel será divergente e vice-versa.
- Se o critério de Sassenfield não for satisfeito a convergência pode ser bastante lenta.
- Uma permutação das linhas do sistema pode reduzir o valor encontrado quando aplicado o critério de Sassenfield.
- A convergência não depende do vetor inicial, porém é evidente que quanto melhor a aproximação do vetor inicial, menor será o número de iterações necessárias para atingir a precisão desejada.
Exemplo:
Resolver o sistema:
Pelo método de Gauss-Seidel com 𝜺<
Critério das linhas
Assim por esse método não é possível garantir a convergência
Aplicando o critério das linhas temos:
Critério de Sassenfeld
Aplicando o critério de Sassenfeld temos:
Como o maior 𝞫 é menor que 1 temos que o critério de Sassenfeld é satisfeito e podemos garantir que o sistema converge pelo processo de Gauss-Seidel
Aplicando vetor inicial
A partir de
Temos: