




Estude fácil! Tem muito documento disponível na Docsity

Ganhe pontos ajudando outros esrudantes ou compre um plano Premium


Prepare-se para as provas
Estude fácil! Tem muito documento disponível na Docsity
Prepare-se para as provas com trabalhos de outros alunos como você, aqui na Docsity
Os melhores documentos à venda: Trabalhos de alunos formados
Prepare-se com as videoaulas e exercícios resolvidos criados a partir da grade da sua Universidade
Responda perguntas de provas passadas e avalie sua preparação.

Ganhe pontos para baixar
Ganhe pontos ajudando outros esrudantes ou compre um plano Premium
Comunidade
Peça ajuda à comunidade e tire suas dúvidas relacionadas ao estudo
Descubra as melhores universidades em seu país de acordo com os usuários da Docsity
Guias grátis
Baixe gratuitamente nossos guias de estudo, métodos para diminuir a ansiedade, dicas de TCC preparadas pelos professores da Docsity
Documento que apresenta o cálculo da armadura longitudinal necessária para um pilar, incluindo as forças normais, índices de esbelteza, momentos mínimos e esbeltezas limites. O documento também inclui o cálculo do momento fletor e da armadura utilizando dois métodos diferentes.
Tipologia: Exercícios
1 / 6

Esta página não é visível na pré-visualização
Não perca as partes importantes!




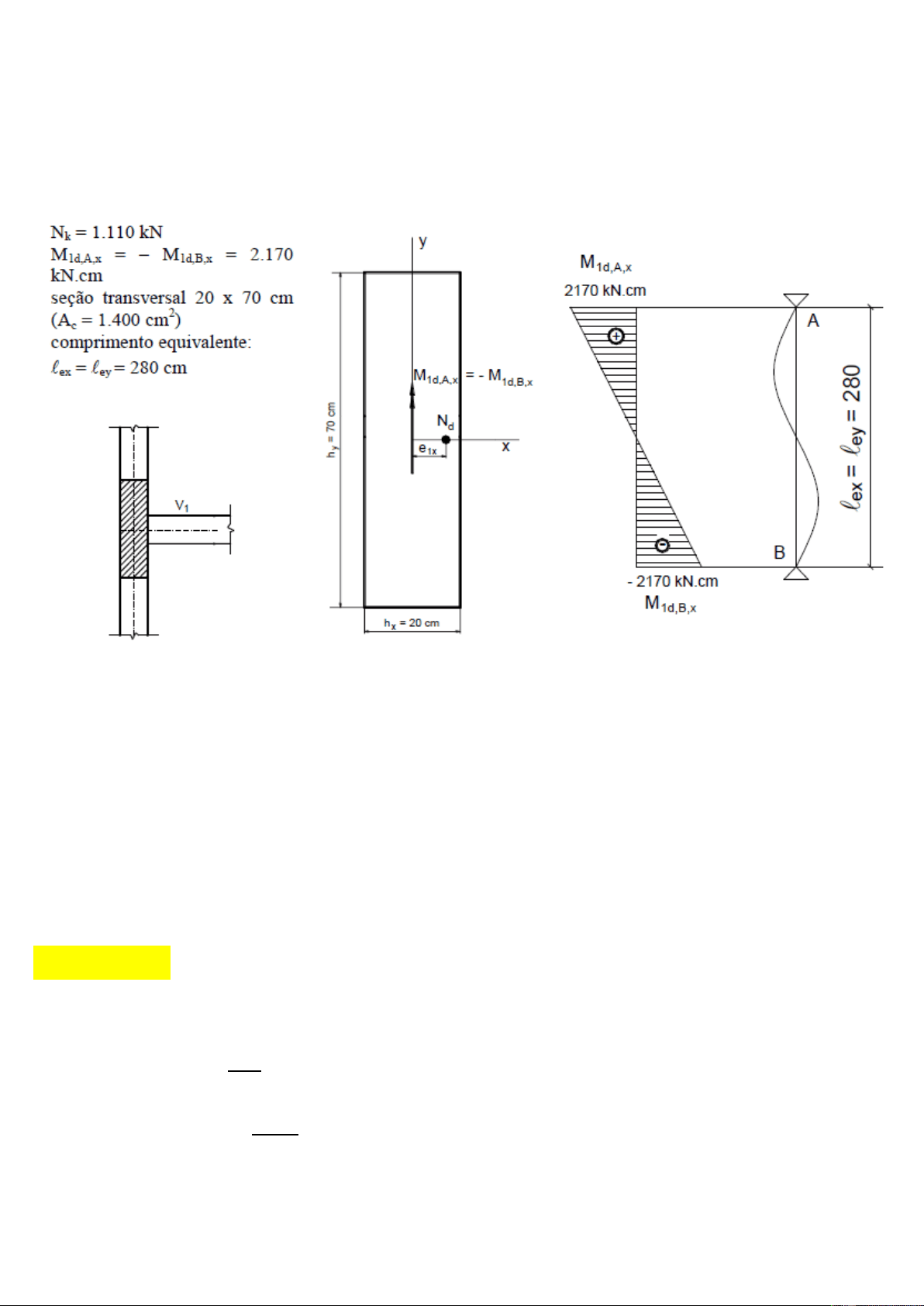
Para o pilar mostrado na Figura, calcular a armadura longitudinal necessária. São conhecidos: C d‘= 4cm CA
M1d,Ax=2170kn.cm
M1d,Bx= -2170kN.cm
a) Força Normal
Nd = γn. γf. Nk
Nd = 1. 1,4. 1110
Nd = 1554 kN
3 , 46.
3 , 46.
M1d,mín = Nd (1,5 + 0,03 h)
M1d,mín = Nd (1,5 + 0,03 h) M1d,mín = 1554 (1,5 + 0,03.20) M1d,mín,x = 3263,4kN.cm
M1d,mín = Nd (1,5 + 0,03 h) M1d,mín = 1554 (1,5 + 0,03.70) M1d,mín,y = 5594,4kN.cm
e) Calculo do momento fletor e da armadura
*Metodo pilar padrão com curvatura aproximada
-Força adimensional
𝜈 =
𝑁𝑑 𝐴𝑐. 𝑓𝑐𝑑
𝜈 =
1554
( 20 ∗ 70 ). (
2 , 5 1 , 4 )
= 0 , 62
*Método do pilar padrão com rigidez k aproximada
𝟏𝟗𝟐𝟎𝟎𝑴𝑺𝒅,𝒕𝒐𝒕^ 𝟐^ + (𝟑𝟖𝟒𝟎𝒉 𝑵𝒅 − 𝝀𝟐^ 𝒉 𝑵𝒅 − 𝟏𝟗𝟐𝟎𝟎𝟎𝜶𝒃𝑴𝟏𝒅,𝑨) 𝑴𝑺𝒅,𝒕𝒐𝒕 − 𝟑𝟖𝟒𝟎𝜶𝒃 𝒉 𝑵𝒅 𝑴𝟏𝒅,𝑨 = 𝟎 𝟏𝟗𝟐𝟎𝟎𝑴𝑺𝒅,𝒕𝒐𝒕^ 𝟐^ + (𝟑𝟖𝟒𝟎. 𝟐𝟎. 𝟏𝟓𝟓𝟒 − 𝟒𝟖, 𝟒𝟐^ 𝟐𝟎 𝟏𝟓𝟓𝟒𝟎 − 𝟏𝟗𝟐𝟎𝟎𝟎 𝟏 𝟑𝟐𝟔𝟑)𝑴𝑺𝒅,𝒕𝒐𝒕 − 𝟑𝟖𝟒𝟎 𝟏 𝟐𝟎 𝟏𝟓𝟓𝟒 𝟑𝟐𝟔𝟑 = 𝟎
𝑴𝑺𝒅,𝒕𝒐𝒕=𝟒𝟗𝟑𝟒𝒌𝑵. 𝒄𝒎
f) calculo da armadura
ц =
ц =