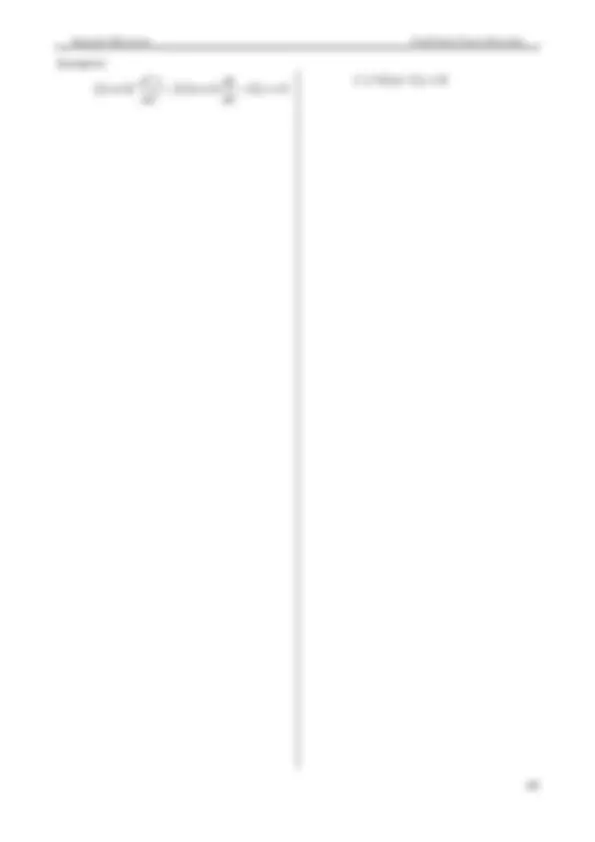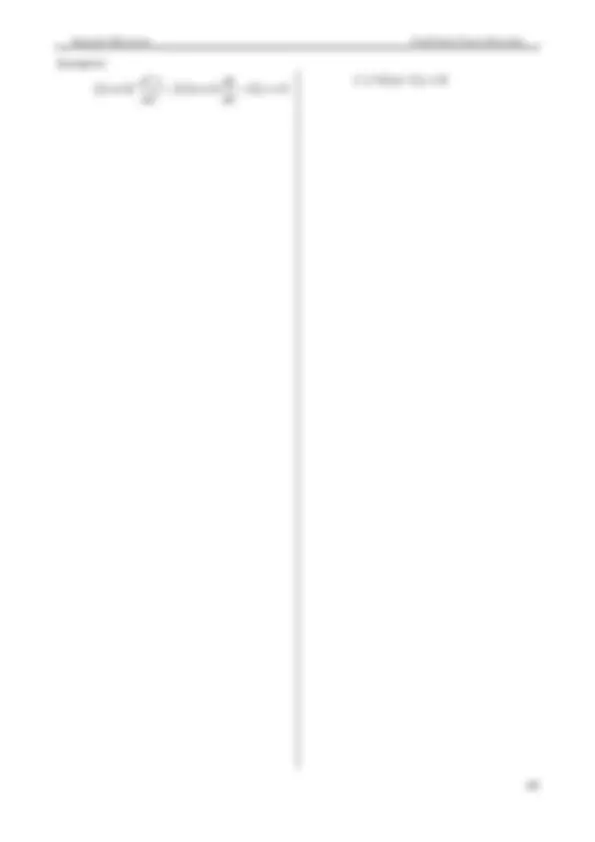EQUAÇÕES DIFERENCIAIS
NOTAS DE AULA
Prof.a Paula Francis Benevides
Ministério da Educação
Universidade Tecnológica Federal do Paraná
Campus Curitiba
Gerência de Ensino e Pesquisa
Departamento Acadêmico de Matemática
Prepare-se para as provas
Estude fácil! Tem muito documento disponível na Docsity
Ganhe pontos para baixar
Ganhe pontos ajudando outros esrudantes ou compre um plano Premium
Guias e Dicas
Prepare-se para as provas
Estude fácil! Tem muito documento disponível na Docsity
Encontrar documentos
Prepare-se para as provas com trabalhos de outros alunos como você, aqui na Docsity
Pesquisar documentos Store
Os melhores documentos à venda: Trabalhos de alunos formados
Videoaulas
Prepare-se com as videoaulas e exercícios resolvidos criados a partir da grade da sua Universidade
Quiz
Responda perguntas de provas passadas e avalie sua preparação.
Ganhe pontos para baixar
Ganhe pontos ajudando outros esrudantes ou compre um plano Premium
Comunidade
Pergunte à comunidade
Peça ajuda à comunidade e tire suas dúvidas relacionadas ao estudo
Ranking universidades
Descubra as melhores universidades em seu país de acordo com os usuários da Docsity
Guias grátis
Os eBooks que salvam estudantes!
Baixe gratuitamente nossos guias de estudo, métodos para diminuir a ansiedade, dicas de TCC preparadas pelos professores da Docsity
/equação diferencial, Esquemas de Empreendedorismo
aaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaa
Tipologia: Esquemas
2020
1 / 169
Esta página não é visível na pré-visualização
Não perca as partes importantes!
Documentos relacionados
Pré-visualização parcial do texto
Baixe /equação diferencial e outras Esquemas em PDF para Empreendedorismo, somente na Docsity!
EQUAÇÕES DIFERENCIAIS
NOTAS DE AULA
Prof.a^ Paula Francis Benevides
Ministério da Educação
Universidade Tecnológica Federal do Paraná
Campus Curitiba
Gerência de Ensino e Pesquisa
Departamento Acadêmico de Matemática
Conteúdo
3.3.1 O determinante 2 2
1 1 a b
3.3.2 O determinante 2 2
1 1 a b
- AULA
- AULA
- 1.1 INTRODUÇÃO
- 1.2 DEFINIÇÃO
- 1.3 CLASSIFICAÇÃO...............................................................................................................
- 1.3.1 Tipo:
- 1.3.2 Ordem:
- 1.3.3 Grau:
- 1.3.4 Linearidade:
- 1.4 ORIGEM DAS EQUAÇÕES DIFERENCIAIS:
- AULA
- RESOLUÇÃO
- 2.1 CURVAS INTEGRAIS:
- 2.2 SOLUÇÃO:
- 2.3 PROBLEMA DE VALOR INICIAL (PVI)
- 2.4 TEOREMA DA EXISTÊNCIA DE UMA ÚNICA SOLUÇÃO
- 2.5 EQUAÇÕES DIFERENCIAIS AUTÔNOMAS.............................................................................
- EQUAÇÕES DE PRIMEIRA ORDEM E PRIMEIRO GRAU
- 3.1 EQUAÇÕES DE VARIÁVEIS SEPARÁVEIS
- 3.1.1 Resolução:
- AULA
- 3.2 EQUAÇÕES HOMOGÊNEAS
- 3.2.1 Função Homogênea
- 3.2.2 Equação Homogênas
- 3.2.2.1 Resolução: .................................................................................................................................................
- 3.2 EQUAÇÕES HOMOGÊNEAS
- AULA
- 3.3 EQUAÇÕES REDUTÍVEIS ÀS HOMOGÊNEAS E EQUAÇÕES REDUTÍVEIS AS DE VARIÁVEIS SEPARADAS. - é diferente de zero a b - é igual a zero. a b
- AULA
- 3.4 EQUAÇÕES DIFERENCIAIS EXATAS
- AULA - 3.4.1 Fator Integrante
- AULA
- 3.5 EQUAÇÕES LINEARES:
- 3.5.1 Fator Integrante:
- 3.5.2 Substituição ou de Lagrange:
- 3.5 EQUAÇÕES LINEARES:
- AULA
- 3.6 EQUAÇÕES NÃO LINEARES DE PRIMEIRA ORDEM REDUTÍVEIS A LINEARES:
- 3.6.1 Equações de Bernoulli:
- 3.6 EQUAÇÕES NÃO LINEARES DE PRIMEIRA ORDEM REDUTÍVEIS A LINEARES:
- AULA - 3.6.2 Equação de Ricatti
- AULA
- EQUAÇÕES DE 1A ORDEM E GRAU DIFERENTE DE UM
- 4.1 ENVOLTÓRIAS E SOLUÇÕES SINGULARES
- 4.1.1 Definições:
- 4.1.2 Equação da Envoltória
- 4.1.3 Soluções Singulares
- AULA - 4.1.4 Equação de Clairaut
- AULA - 4.1.5 Equação de Lagrange: - 4.1.6 Outros tipos de equação de 1a Ordem e grau diferente de um:
- AULA
- EXERCÍCIOS GERAIS................................................................................................
- AULA
- EQUAÇÕES DIFERENCIAIS COM MODELOS MATEMÁTICOS
- 6.1 MODELO MATEMÁTICO
- 6.2 DINÂMICA POPULACIONAL
- 6.3 MEIA VIDA
- 6.4 DECAIMENTO RADIOTAIVO
- 6.5 CRONOLOGIRA DO CARBONO
- 6.6 RESFRIAMENTO
- 6.7 MISTURAS
- 6.8 DRENANDO UM TANQUE
- 6.9 DISSEMINAÇÃO DE UMA DOENÇA
- 6.10 CORPOS EM QUEDA
- 6.10.1 Corpos em queda e a resistência do ar
- 6.11 CORRENTE DESLIZANTE
- 6.12 CIRCUITOS EM SÉRIE
- AULA
- EQUAÇÕES DIFERENCIAIS LINEARES DE 2A ORDEM E ORDEM SUPERIOR
- AULA
- 7.1 EQUAÇÕES LINEARES E HOMOGÊNEAS DE COEFICIENTES CONSTANTES
- 7.1.1 Caso 1: Raízes Reais Distintas.
- 7.1.2 Caso 2: Raízes Múltiplas.
- 7.1.3 Caso 3: Raízes complexas distintas.
- 7.1 EQUAÇÕES LINEARES E HOMOGÊNEAS DE COEFICIENTES CONSTANTES
- AULA
- 7.2 EULER - CAUCHY...........................................................................................................
- AULA
- 7.3 EQUAÇÕES LINEARES NÃO HOMOGÊNEAS
- 7.3.1 Solução por coeficientes a determinar (Descartes):
- 7.3 EQUAÇÕES LINEARES NÃO HOMOGÊNEAS
- AULA - 7.3.2 Solução por variação de parâmetros
- AULA - 7.3.3 Método do Operador Derivada - 7.3.3.1 Definição ................................................................................................................................................. - 7.3.3.2 Propriedades ........................................................................................................................................... - 7.3.3.3 Equações Diferenciais ............................................................................................................................. - 7.3.3.4 Operador Anulador ................................................................................................................................. - 7.3.3.5 Coeficientes indeterminados - Abordagem por Anuladores ................................................................... - 7.3.3.6 Resolução de Equações Lineares ............................................................................................................
- AULA
- EXERCÍCIOS GERAIS..............................................................................................
- AULA
- MODELAGEM COM EQUAÇÕES DIFERENCIAIS DE ORDEM SUPERIOR
- 9.1 EQUAÇÕES LINEARES - PROBLEMAS DE VALOR INICIAL:
- 9.1.1 Sistema Massa-Mola: Movimento Livre não amortecido
- 9.1.1.1 ED do Movimento Livre não amortecido: ...............................................................................................
- 9.1.1.2 Solução e Equação do Movimento:.........................................................................................................
- 9.1.2 Sistema Massa-Mola: Movimento Livre Amortecido
- 9.1.2.1 ED do Movimento Livre Amortecido: ......................................................................................................
- 9.1.3 Sistema Massa Mola: Movimento Forçado
- 9.1.3.1 ED do Movimento Forçado com Amortecimento: ..................................................................................
- 9.1.3.2 ED de um Movimento Forçado Não Amortecido: ...................................................................................
- 9.1.4 Circuito em Série Análogo - Circuitos elétricos RLC em série
- 9.1.1 Sistema Massa-Mola: Movimento Livre não amortecido
- 9.2 EQUAÇÕES LINEARES - PROBLEMAS DE CONTORNO.............................................
- 9.2.1 Deflexão de uma viga:
- 9.2.1.1 Soluções Não Triviais do Problema de Valores de Contorno: .................................................................
- 9.2.1.2 Deformação de uma Coluna Fina: ...........................................................................................................
- 9.2.1.3 Corda Girando: ........................................................................................................................................
- 9.2.1 Deflexão de uma viga:
- AULA
- SISTEMA DE EQUAÇÕES DIFERENCIAIS
- 10.1 SISTEMA CANÔNICO E SISTEMA NORMAL:............................................................
- AULA
- 10.2 SISTEMAS DE EQUAÇÕES DIFERENCIAIS NA FORMA SIMÉTRICA...........................
- AULA
- 10.3 MATRIZES E SISTEMAS DE EQUAÇÕES LINEARES DE PRIMEIRA ORDEM
- 10.3.1 Vetor solução
- 10.3.2 O Problema de Valores Iniciais
- 10.3.2.1 Existência de uma única solução ...........................................................................................................
- 10.3.3 Sistemas homogêneos
- 10.3.3.1 Princípio da Superposição .....................................................................................................................
- 10.3.4 Independência Linear
- 10.3.4.1 Critério para Soluções Linearmente Independentes .............................................................................
- 10.3.5 Conjunto fundamental de solução
- 10.3.5.1 Solução Geral - Sistemas Homogêneos .................................................................................................
- 10.3.6 Sistemas não homogêneos
- 10.3.6.1 Solução Geral - Sistemas Não-Homogêneos .........................................................................................
- 10.3.7 Uma Matriz Fundamental................................................................................
- 10.3.7.1 Uma Matriz Fundamental é Não-Singular .............................................................................................
- 10.3.7.2 Matriz Especial ......................................................................................................................................
- 10.3.7.3 t é uma Matriz Fundamental........................................................................................................
- 10.3 MATRIZES E SISTEMAS DE EQUAÇÕES LINEARES DE PRIMEIRA ORDEM
- AULA
- 10.4 SISTEMAS LINEARES HOMOGÊNEOS
- 10.4.1 Autovalores reais e distintos
- 10.4.2 Autovalores complexos
- 10.4.3 Autovalores de Multiplicidade dois
- 10.4 SISTEMAS LINEARES HOMOGÊNEOS
- AULA
- 10.5 SISTEMAS NÃO HOMOGÊNEOS
- 10.5.1 Coeficientes Indeterminados
- 10.5.2 Variação de Parâmetros
- 10.5 SISTEMAS NÃO HOMOGÊNEOS
- AULA
- RESOLUÇÃO POR SÉRIES DE POTÊNCIA:.............................................................
dx
x a
x a
2 2
2 2
R: C
a
x
x 2 a arctan
15) xe^3 xdx R: e x^ 3 x 1 C
dx
x x
x
(^) 2 R: 2 ln x 2 x 1 C
dx
x x
x x
2 3
2
R: ln x 3 x 1 C 3
dx
x
x
R: ln 1 x arctan x C
x x
xdx
R: ln 1 3 x 2 C 2
dx
x
x
R: x ln 5 x 3 C
dx
x x
x
2 R: 2 ln 5 x 4 x 1 arctan( 5 x 2 ) C
dx
x
x
R: 2 x 21 ln x 10 C
23) e x^ .( x 2 ) dx
ln^1 R: x x C 2 ln
dx
x
x
e arctan x 2
arctan
. R: ^ x e C
x arctan arctan 1.
25) e xdx
x .sin lncos
R: C
x
sin 2
26) e ^ x^ ( 2 x^3 ) dx
2 R: x e ^ x^ C
2 ( 2 1 ).
dx
e x x
x
2 2
R: C
e x x
x
^
2 2
28) e^ x dx
( 2 x^. 4 2 ) R: x x e C x 2 2 ( 2 2 1 ).
AULA 2
EQUAÇÕES DIFERENCIAIS
1.1 INTRODUÇÃO
Antes de mais nada, vamos recordar o que foi aprendido em Cálculo!!! A derivada dydx
de uma função 𝑦 = 𝜑(𝑥) nada mais é do que uma outra função 𝜑′(𝑥) encontrada por uma regra
apropriada. Como por exemplo, a função 𝑦 = 𝑒𝑥 3 é diferenciável no intervalo (−∞, ∞), e a sua
derivada é. 3 2
3
e x
dx
dy x
. Se fizermos
x^3 y e teremos:
y. 3 x^2
dx
dy
Vamos supor agora que seu professor lhe desse a equação (1) e perguntasse qual é a função representada por y? Apesar de você não fazer ideia de como ela foi construída, você está a frente de um dos problemas básicos desta disciplina: como resolver essa equação para a desconhecida função 𝑦 = 𝜑(𝑥)? O problema é semelhante ao familiar problema inverso do cálculo diferencial, onde dada uma derivada, encontrar uma antiderivada. Não podemos deixar de lado a diferença entre a derivada e a diferencial, pois, embora a derivada e a diferencial possuam as mesmas regras operacionais, esses dois operadores têm significados bastante diferentes. As diferenças mais marcantes são: a derivada tem significado físico e pode gerar novas grandezas físicas, como por exemplo a velocidade e a aceleração; a diferencial é um operador com propriedades puramente matemáticas; a derivada transforma uma função em outra, mantendo uma correspondência entre os pontos das duas funções (por exemplo, transforma uma função do segundo grau em uma função do primeiro grau); a diferencial é uma variação infinitesimal de uma grandeza; a derivada é uma operação entre duas grandezas; a diferencial é uma operação que envolve uma grandeza; o resultado de uma derivada não contém o infinitésimo em sua estrutura; consequentemente, não existe a integral de uma derivada; a integral só pode ser aplicada a um termo que contenha um diferencial (infinitésimo); se for feito o quociente entre os dois diferenciais, tem-se:
dx
dy
em total semelhança com a definição de derivada. A consequência direta desse fato é que a derivada não é o quociente entre duas diferenciais, mas comporta-se como se fosse esse quociente. Isto significa que a partir da relação:
f ( x )
dx
dy
é possível escrever:
dy f ( x ) dx
que se denomina equação diferencial. uma das aplicações mais importantes envolvendo derivadas e diferenciais é a obtenção da equação diferencial, etapa fundamental para a introdução do Cálculo Integral.
3
3 3
3
dx
d y
y
dx
d y
x 3
(^23)
3
3
dx
d y
y
dx
d y
x
3 a^ ordem e 2o^ grau
x y
dx
dy
ln ln^2 y
x
dx
dy
ln 2 ^ ey dx
dy x
. 1 2
x ey
dx
dy 2
1 a^ ordem e 1o^ grau
Observe que nem sempre à primeira vista, pode-se classificar a equação de imediato quanto a ordem e grau.
1.3.4 LINEARIDADE:
Dizemos que uma equação diferencial ordinária
1
1 a x y g x
dx
dy
a x
dx
d y
a x
dx
d y
a x n
n n n
n
n ^
de ordem n é linear quando são satisfeitas as seguintes condições:
1) A variável dependente y e todas as suas derivadas y ', y ",, yn são do primeiro grau, ou
seja, a potência de cada termo envolvendo y é um.
2) Os coeficientes a 0 , a 1 ,, an de y ' , y ",, yn dependem quando muito da variável
independente x.
Exemplos:
a)( y x ) dx 8 xdy 0
b) 2 7 0
2
y
dx
dy
dx
d y
c) y x
dx
dy
x
dx
d y
3
São respectivamente equações diferenciais ordinárias lineares de primeira, segunda e terceira ordem.
1.4 ORIGEM DAS EQUAÇÕES DIFERENCIAIS:
Uma relação entre as variáveis, encerrando n constantes arbitrárias essenciais, como
y x^4 Cx ou y Ax^2 Bx , é chamada uma primitiva. As n constantes, representadas sempre
aqui, por letras maiúsculas, serão denominadas essenciais se não puderem ser substituídas por um número menos de constantes. Em geral uma primitiva, encerrando n constantes arbitrárias essenciais, dará origem a uma equação diferencial, de ordem n , livre de constantes arbitrárias. Esta equação aparece eliminando-se
as n constantes entre as (^ n ^1 )equações obtidas juntando-se à primitiva as n equações provenientes
de n derivadas sucessivas, em relação a variável independente, da primitiva.
Obter a equação diferencial associada às primitivas abaixo:
a) x C
x
y
b) y C 1 senx C 2 cos x
c) y Cx^2
d) y C 1 x^2 C 2
e) y a cos( x b )onde a e b são constantes
f) y C 1 e^3 x^ C 2 e^ ^2 x
AULA 3
2. RESOLUÇÃO
Resolver uma ED é determinar todas as funções que, sob a forma finita, verificam a equação, ou seja, é obter uma função de variáveis que, substituída na equação, transforme-a numa identidade. A resolução de uma equação diferencial envolve basicamente duas etapas: a primeira, que é a preparação da equação, que consiste em fazer com que cada termo da equação tenha, além de constantes, um único tipo de variável. A segunda etapa é a resolução da equação diferencial e consiste na aplicação dos métodos de integração.
2.1 CURVAS INTEGRAIS:
Geometricamente, a primitiva é a equação de uma família de curvas e uma solução particular é a equação de uma dessas curvas. Estas curvas são denominadas curvas integrais da equação diferencial.
x
dx
dy
2.2 SOLUÇÃO:
É a função que quando substituída na equaçãodiferencial a transforma numa identidade. As soluções podem ser: Solução geral: A família de curvas que verifica a equação diferencial, (a primitiva de uma equação diferencial) contem tantas constantes arbitrárias quantas forem as unidades de ordem da equação. Solução particular: solução da equação deduzida da solução geral, impondo condições iniciais ou de contorno. Geralmente as condições iniciais serão dadas para o instante inicial. Já as condições de contorno aparecem quando nas equações de ordem superior os valores da função e de suas derivadas são dadas em pontos distintos. Solução singular: Chama-se de solução singular de uma equação diferencial à envoltória da família de curvas, que é a curva tangente a todas as curvas da família. A solução singular não pode ser deduzida da equação geral. Algumas equações diferenciais não apresentam essa solução. Esse tipo de solução será visto mais adiante.
As soluções ainda podem ser:
Solução explícita: Uma solução para uma EDO que pode ser escrita da forma y f(x) é chamada solução explícita. Solução Implícita: Quando uma solução pode apenas ser escrita na forma G( x,y) 0 trata-se de uma solução implícita.
Exemplo:
Consideremos a resolução da seguinte EDO: x
dx
dy
y x x c
dy xdx
^ (^32)
A solução geral obtida é obviamente uma solução explicita.
Por outro lado, pode-se demonstrar que a EDO:
2
2
xy x
y dx
dy
^ tem como solução: x
y
y Ce , ou seja, uma solução implícita.
Exemplo:
Verifique que
x
y
4
é uma solução para a equação^2
1 xy dx
dy no intervalo ( , ).
Resolução: Uma maneira de comprovar se uma dada função é uma solução é escrever a equação
diferencial como xy 0 dx
dy (^12) e verificar, após a substituição, se a diferença acima^2
1 xy dx
dy é
zero paratodo x no intervalo.
x
dx
dy
4 x
dx
dy 3 3
Substituindo na E.D., temos
3 4 12 3 2 3 3
^
x x x
x
x x
x
x
Esta condição se verifica para todo x R
2.3 PROBLEMA DE VALOR INICIAL (PVI)
Seja a equação diferencial de primeira ordem f (^ x , y )
dx
dy
sujeita a condição inicial
y( x 0 ) y 0 , em que x 0 é um número no intervalo I e y 0 é um número real arbitrário, é chamado de
problema de valor inicial. Em termos geométricos, estamos procurando uma solução para a equação diferencial definida em algum intervalo I tal que o gráfico da solução passe por um ponto (xo, yo) determinado a priori.
Teorema: Considere o problema de valor inicia
( 0 ) 0
( ) ( ) yx y
px y qx dx
dy
Se p(x) e q(x) são continuas em um intervalo aberto I e contendo x (^) 0 , então o problema de
valor inicial tem uma única solução nesse intervalo.
Alertamos que descobrir uma solução para uma Equação Diferencial é algo “similar” ao cálculo de uma integral e nós sabemos que existem integrais que não possuem primitivas, como é o caso das integrais elípticas. Dessa forma, não é de se esperar que todas as equações diferenciais possuam soluções.
2.5 EQUAÇÕES DIFERENCIAIS AUTÔNOMAS
As equações diferenciais da forma
f y
dx
dy
são chamadas de autônomas.
Utilizando a manipulação formal introduzida por Liebnitz (1646-1716), podemos escrever a equação (2) na forma:
dx f y
dy
Cuja resolução é:
y
y
dy f y
x y x y 0 ( )
1 ( ) ( 0 ) (4)
Para justificar a equação (4) necessitamos que
f y
seja bem definida no intervalo de
interesse A, onde f (^ y )^0 e que seja contínua neste intervalo A. Pois, como 0
dy f y
dx
em
A , o Teorema da Função Inversa garante que existe uma função inversa da função x (^ y ), isto é,
y F ( x ) tal que f ( y )
dx
dF
em A , o que justifica o procedimento formal.
Portanto, a solução do problema de condição inicial
yx y
f y
dx
dy
é obtida pela solução do problema
x y x
dy f y
dx
e com a inversão da função x ( y ).
As equações autônomas aparcem na formulação de uma grande quantidade de modelos. Sempre que uma lei de formação afrma que: “a taxa de variação de uma quantidade y(t) é proporcional a esta mesma quantidade” , temos uma equação autônoma da forma
ky
dx
dy
Como, f ( y ) ky , então f ( y *) 0 se y * 0. Devemos procurar soluções separadamente
nos dois intervalos y 0 e 0 y .
Considerando inicialmente o problema de Cauchy
y ( x 0 ) y 0 0
ky
dx
dy
E seu problema inverso
x y x
dy ky
dx
Cuja solução inversa é dada por
y
x y x y y
y
k
y y x
k
dy x
ky
dy C x
ky
x y
0 0 0 0
0 0 0 0 ( )
ln
ln ln
ou seja, ( ) 0 0 0
ln k ( x x ) y y ekxx^0
y
y
^ para^ x R.
Considere a equação autônoma
ky a
dx
dy
sua solução geral, para
k
a
y , é obtida considerando-se sua forma diferencial
1) 3 x 1
dx
dy
2) ydx xdy 0
dy
y
x
xdx
4) tgx .sec ydx tgy sec xdy 0
5) ( x^2 1 ) 1 y^2 dx x^2 dy 0
x xy
y
dx
dy
2
2
2
1
1 x
y dx
dy