Energia cinetica potencial resumo, Resumos de Engenharia Química

Baixe Energia cinetica potencial resumo e outras Resumos em PDF para Engenharia Química, somente na Docsity!



Como que você definiria trabalho?



Provavelmente você responderia um

esforço mental ou físico realizado por uma

pessoa ou uma máquina.



Não está errado, mas vamos ver como

ficaria a definição de trabalho em mecânica.



O trabalho é realizado por uma força e

precisa ter outras condições para que seja

realizado um trabalho

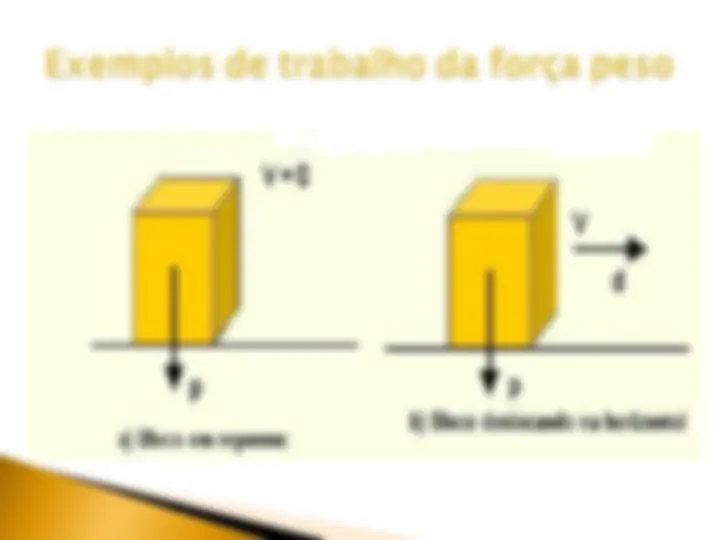
 Quando você está parado carregando qualquer coisa. A força que realizaria trabalho, por exemplo, seria a força peso, mas como não está havendo deslocamento, não há realização de trabalho.  (^) Você faz um deslocamento horizontal, carregando alguma coisa. Novamente a força peso não realizaria trabalho porque precisa haver força ou componente da força na direção do deslocamento, o que não acontece com a força peso porque ela atua na vertical.  (^) Se você subir uma rampa, a força peso realizaria trabalho porque tem componente na direção do deslocamento



"É o produto da força ou componente da força na

direção do deslocamento, pelo deslocamento".  (^) Notação : T (trabalho) Expressão: T = F. d  Observe que o trabalho é uma grandeza escalar porque é decorrente do produto escalar de duas grandezas vetoriais F e d.  (^) Quando a força atua na direção do deslocamento o trabalho é simplesmente o produto do módulo da força pelo módulo do deslocamento  T = F d

 (^) U (T) = U (F). U (L)  (^) (unidade de trabalho) = unidade de força x unidade de comprimento  (^) No Sistema Internacional a unidade de força (U (F)) é 1 newton ( N) e a do comprimento (U(L)) 1 metro (1 m), portanto:  (^) U (T) = 1 newton x 1m = 1 joule (1 J)  (^) A esta unidade de trabalho, 1 N x 1 m, deram o nome de 1 joule (1 J) em homenagem a James Prescott Joule (1818 - 1889), físico inglês que fêz pesquisas mostrando que o calor é uma forma de energia.  (^) 1 joule é o trabalho realizado por uma força de 1 N para deslocar o bloco a uma distância de 1 m.

Energia

é a capacidade

de realizar trabalho.

 (^) está associada ao movimento do corpo (cine = movimento).  (^) Quando a força resultante ( F ) que atua sobre o carro de massa m é não nula, esta imprime uma aceleração a, fazendo com que haja variação da velocidade do corpo.  (^) Quanto maior a velocidade do carro, maior a energia cinética.  (^) Considerando um caminhão que tivesse a mesma velocidade do carro, mas possui maior massa, maior também será o trabalho realizado, ou seja , maior a energia cinética.  (^) Você pode observar esta situação em uma colisão do carro e do caminhão com um poste.  (^) Na colisão do caminhão com o poste, o trabalho é maior, do que o do carro com o poste. Obviamente o carro vai ficar mais danificado.

 (^) O trabalho realizado pela força F é dado como sendo o produto da força (F) pelo deslocamento (x):  T = F x  (^) Como F = m a  (^) T = m a x (3)  Substituindo 1 e 2 em 3, obtemos:  (^) T = m (v - v 0 ) / t ( (v + v 0 ) / 2) t  (^) T = m (v2 - v 0



T = ((m v^2 /2) - (m v 02 /2)) (4)



A metade do produto da massa pelo

quadrado da velocidade é a energia cinética

(Ec) do corpo:



Ec=( m v^2 )/2 (5)



Substituindo em (4) , temos:



T = Ec (final) - Ec

(inicial) (6)

 Quando um objeto de massa m está a uma determinada altura em relação a um nível de referência, ele tem capacidade de realizar um trabalho; esta energia associada à posição que o objeto está que é denominada energia potencial gravitacional (Ep).  (^) A energia potencial gravitacional (Ep) é calculada como sendo o produto do peso do objeto pela altura que ele está em relação a um nível de referência:  (^) Ep = p h = m g h (7)

 (^) A energia mecânica (Emec) de um sistema é a soma da energia cinética e da energia potencial.  (^) Quando um objeto está a uma altura h, como já foi visto, ele possui energia potencial; à medida que está caindo, desprezando a resistência do ar, a energia potencial gravitacional do objeto que ele possui no topo da trajetória vai se transformando em energia cinética e quando atinge o nível de referência a energia potencial é totalmente transformada em energia cinética.  (^) Este é um exemplo de conservação de energia mecânica.

 (^) Na ausência de forças disssipativas, a energia mecânica total do sistema se conserva, ocorrendo transformação de energia potencial em cinética e vice-versa.  (^) Podemos escrever:  (^) E mec = E p + E c = constante (9) onde E p = mgh e Ec =( m v^2 )/  Substituindo, obtemos:  E mec = mgh + ( m v^2 )/2 = constante ou E mec / m = gh + v^2 /2 = constante (10)

Considere que o objeto que está caindo e possui 10 kg de massa e está a uma altura de 10 m do nível de referência  (^) No topo, o objeto possui uma energia potencial:  (^) Ep (inicial) = mgh = 10 9,8 10 = 980 J (1)  e energia cinética:  (^) Ec (inicial)=( m v (^2) )/2 = 0 J (v = 0 m/s) (2)