























Estude fácil! Tem muito documento disponível na Docsity

Ganhe pontos ajudando outros esrudantes ou compre um plano Premium


Prepare-se para as provas
Estude fácil! Tem muito documento disponível na Docsity
Prepare-se para as provas com trabalhos de outros alunos como você, aqui na Docsity
Os melhores documentos à venda: Trabalhos de alunos formados
Prepare-se com as videoaulas e exercícios resolvidos criados a partir da grade da sua Universidade
Responda perguntas de provas passadas e avalie sua preparação.

Ganhe pontos para baixar
Ganhe pontos ajudando outros esrudantes ou compre um plano Premium
Comunidade
Peça ajuda à comunidade e tire suas dúvidas relacionadas ao estudo
Descubra as melhores universidades em seu país de acordo com os usuários da Docsity
Guias grátis
Baixe gratuitamente nossos guias de estudo, métodos para diminuir a ansiedade, dicas de TCC preparadas pelos professores da Docsity
Estudo realizado sobre os esforções atuantes num conduto forçado de PVC de secção constante e morfologia retilínea. Examina os dados extraídos de extensômetros (strain gages) com base nos cálculos de Mecânica dos Sólidos. São objeto de seu estudo a demonstração dos cálculos teóricos na aplicação prática, cujo escopo é o bom dimensionamento dos condutos, bem como a integração com os conhecimentos de Mecânica dos Fluidos.
Tipologia: Manuais, Projetos, Pesquisas
1 / 30

Esta página não é visível na pré-visualização
Não perca as partes importantes!























Rháfaga Barros Willian Molissani Fábio di Grigoli Kaique Onofre Vitor Arcas Henrique Moreno
Rháfaga Barros [12.112.681-7] Willian Molissani [12.212.262-5] Fábio di Grigoli [12.213.285-5] Kaique Onofre[12.212.224-5] Vitor Arcas [12.115.507-1] Henrique Moreno [12.212.213-8]
Relatório técnico apresentado como requisito parcial para obtenção da aprovação na disciplina NM.6610 – Mecânica dos Sólidos I no curso de Engenharia Mecânica, no Centro Universitário da FEI. Prof. Me. João José de Souza
Imagem 1 .......................................................... esquematização do projeto (desenho próprio)
Imagem 2 .................................................. detalhe da instalação dos gages (desenho próprio)
Imagem 3 ............................................... detalhe do conduto instrumentado (foto do projeto)
Imagem 4 ............................................... detalhe do conduto instrumentado (foto do projeto)
Imagem 5 ........... manômetro utilizado como ponto de partida nos cálculos (foto do projeto)
Imagem 6 ............................. formação do escoamento turbulento (retirado da bibliografia 2)
Imagem 7 ............................................. atrito partículas/superfície (retirado da bibliografia 3)
Imagem 8 ................................................... rugosidade do material (retirado da bibliografia 2)
Imagem 9 ............................................................ válvula globo (retirado na internet, apócrifo)
Imagem 10 ............................................................ redução abrupta (retirado da bibliografia 2)
Imagem 11 ............................................................. conversão à 90º (retirado da bibliografia3)
Imagem 12 ................. elementos contribuintes da perda de carga (retirado da bibliografia 3)
Imagem 13 ........................................... strain gauge ampliado (retirado da internet, apócrifo)
Imagem 14 ........................... princípio de funcionamento do gage ( retirado da bibliografia 7)
𝑅𝑒 ............................................................................................................... número de Reynolds 𝜌 ................................................................................................................................. densidade 𝑣 ....................................................................................................... velocidade do escoamento 𝜇 ................................................................................................ viscosidade dinâmica do fluido 𝑔 ........................................................................................................... aceleração da gravidade 𝐷𝐻 ............................................................................................................. diâmetro do conduto 𝐿 ........................................................................................................ comprimento do conduto ℎ𝑓 ...................................................................................................... perda de carga distribuída ℎ𝑠 .......................................................................................................... perda de carga singular 𝑘𝑠 .................................................................................. coeficiente de perda de carga singular 𝐻 1 ....................................................................... carga manométrica na secção do manômetro 𝐻 2 ....................................................................... carga manométrica na secção instrumentada Q* ................................................................................................................... vazão volumétrica Q ..................................................................................................................... momento estático V ............................................................................................................................ força cortante N .............................................................................................................................. força normal J ....................................................................................................................... momento angular I ................................................................................................................... momento de inércia
Para o correto dimensionamento de tubulações forçadas é fundamental ter conhecimento não só do fluido escoador e pressão, mas também dos esforços solicitantes na própria tubulação. Esforços estes oriundos por parte da própria natureza dos escoamentos turbulentos (Re > 2.400) – os quais geram não só tensões cisalhantes devido a viscosidade do fluido, como também tensões normais ortogonais ao sentido do escoamento – assim como forças oriundas do equacionamento da quantidade de movimento num ponto de conversão de sentido ou ao deixar o conduto forçado.
Com o auxílio da extensometria e aliado aos conhecimentos de Mecânica dos Sólidos e Mecânica dos Fluidos, é possível determinar todos os esforços atuantes e suas causas geradoras para não só um bom dimensionamento de projeto, como também uma boa base teórica dos porquês intrínsecos ao fenômeno.
HIDRÁULICA/INSTALAÇÃO
a. Bomba centrífuga RUDC RF-5 3/2HP; b. Tubulação metálica 2”, 3/2”, 1”; c. Tubulação PVC Amanco 1”, 3/4"; d. Válvula tipo esfera DECA 3/4"; e. Termômetro analógico graduado em escala ºF;
APARELHAMENTO
f. Strain gauge PA-06-125AA-120L; g. Strain indicator Micro-Measurements VPG – P3;
CONSTRUÇÃO GRÁFICA
h. Software gráfico Inventor 2014 (para elaboração da perspectiva).
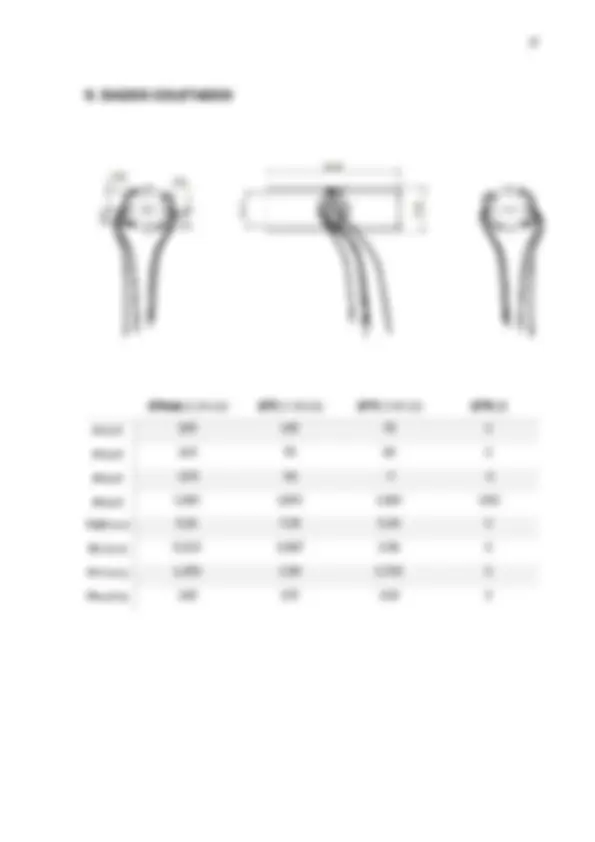
Imagem 3 – Detalhe do conduto instrumentado
Imagem 4 – Detalhe do conduto instrumentado
Imagem 5 – Manômetro utilizado como ponto de partida nos cálculos
O processo pelo qual ocorre o escoamento pelo conduto forçado se inicia no bombeamento da água, o motor elétrico transforma energia elétrica em movimento mecânica por meio da indução de campos magnéticos girantes, os cais induzem o rotor a movimentar- se ordenadamente numa velocidade definida pelo número de polos eletromagnéticos, as perdas na conversão de energia elétrica em energia mecânica são relativamente pequenas (da ordem de 15%) devido basicamente ao atrito nos mancais, correntes parasitas de Foucault e devido a indutância, sendo este último não exatamente uma perda, mas sim uma variável que entra no cálculo da potência reativa, potência que não gera nenhum trabalho útil.
Após a transformação da energia elétrica em mecânica, o eixo do motor é acoplado ao cabeçote da bomba, cuja função é transferir parte dessa energia mecânica para o fluido, as principais perdas nessa etapa são basicamente devido ao atrito nos mancais, a vibração do rotor e as imperfeições (rugosidades) na câmara de entrada/saída e do próprio rotor.
Não é objetivo deste trabalho calcular estas perdas devido à falta de correlação com a proposta do estudo, partiremos de um volume de controle a partir da seção com manômetro mais próxima do conduto instrumentado, dado que muitas interferências e contratempos e ainda falta de um manômetro funcional e garantido no laboratório de mecânica dos fluidos nos impediu de monta-lo anterior à seção estudada.
7.1. CONSIDERAÇÕES/HIPÓTESES DO PROJETO
Para uma simplificação dos cálculos e redução do número de variáveis, trabalharemos com as seguintes hipóteses: regime permanente, fluido incompressível, condutos cilíndricos constantes, rugosidade uniforme, temperatura constante/sem troca de calor.
Desta forma temos que as perdas se darão pelo puro atrito entre o fluido e o conduto forçado. É possível calcular esta perda pela fórmula da perda de carga distribuída, à saber:
ℎ𝑓 = 𝑓 𝐷𝐿 𝐻
Calculo este que não será realizado, uma vez que não é o escopo do trabalho, servirá apenas de conhecimento agregado para que o leitor possa buscar aprofundamento no assunto.
7.3. PERDAS DE CARGA LOCAIS OU SINGULARES
Além das perdas de cargas distribuídas, as quais se caracterizam pela perda numa tubulação retilínea, há também as perdas singulares, perdas que se concentram em um ponto específico. Estas perdas estão associadas a elementos que produzem um atrito maior que o simples atrito numa tubulação retilínea, como a transferência de energia por quantidade de movimento, por exemplo, um cotovelo à 90º causará não só atrito entre o fluido e a conexão, como também uma transferência de energia ao cotovelo pelo impacto que o fluido realizará ao fazer a conversão. Noutras palavras, é uma perturbação brusca no escoamento do fluido.
Com a ajuda de uma tabela de perdas e de comprimentos virtuais de tubulações que geram perdas singulares obtivemos dados de comprimento de tubulação equivalente à tais perdas, no TE de 2” e no cotovelo de raio médio, de ¾”
Image 7 – Atrito partículas/superfície.
Image 8 – Rugosidade do material.
Segue alguns exemplos de perdas singulares, ou locais:
De mesmo modo, é possível calcular estas perdas em cada caso, a fórmula que será utilizada no cálculo das perdas singulares será:
ℎ𝑠 = 𝑘𝑠2𝑔^ 𝑣²
Image 9 – Válvula Globo.
Image 10 – Redução abrupta. Image 11 – Conversão à 90º.
Tabela 1 – Coeficiente Ks de singularidades
7.4. FUNCIONAMENTO DO STRAIN GAUGE
O strain gage é um dispositivo cuja resistência elétrica varia proporcionalmente às forças de tração e compressão que estão sendo exercidas sobre ele. Medições de tensão mecânica envolvem tipicamente variações muito pequenas na resistência, quantidades da ordem de millistrain. Existe vários tipos de ligação em ponte do strain gages, a usada no experimento foi a de ¼ de ponte devido ao tipo de deformação.
Image 13 – Strain gauge ampliado. Image 14^ –^ Princípio de funcionamento do gage
Logo após a montagem do cano instrumentado e suas partes na saída do bocal de 2”, os fios respectivos dos gages foram ligados nos conectores de entrada do aparelho leitor dos dados de microdeformações, o VPG – P3, e então os valores de leitura foram zerados, posteriormente foram colocados na tabela de dados em Q*0, onde percebe-se que os extensômetro número 4, transversal, teve problemas de variação numérica após algumas tentativas de zerar todos e, provavelmente, se danificou durante o processo de colagem na superfície do PVC estudado, portanto não iremos considera-lo para fins de cálculo.
A bomba foi ligada em vazão máxima e os dados de pressão de manômetros e vazão de agua pelo conduto, assim como as microdeformações no cano instrumentado foram anotadas, o mesmo procedimento ocorre ao variar a vazão fechando uma das válvulas.
10.1. DETERMINAÇÃO DAS PERDAS DE CARGA E ESFORÇOS POR MECÂNICA
DOS FLUIDOS.
Eq. De Bernoulli:
𝐻1 = 𝑣1 2∗𝑔^2 + 𝑃1𝛾 + 𝑧
𝐻2 = 𝐻1 − 𝐻𝑝𝑒𝑟𝑑𝑎𝑠
𝐻2 = (^) 2∗𝑔𝑣1^2 + 𝑃1𝛾 + 𝑧1 − (^) 2∗𝑔𝑣1^2 [𝑓(𝑄) 𝐿𝑣𝑖𝑟𝑡𝑢𝑎𝑙𝐷𝑖 ]
Eq. Quantidade de Movimento:
𝐹𝑠 = −[𝑃1𝐴1𝑛1 + 𝑃2𝐴2𝑛2 + 𝑄 ∗ (𝑣2 − 𝑣1) + 𝐺)]
Para a vazão máxima:
𝐻1(𝑞𝑚á𝑥) = (^) 2∗9,83,8^2 + (^128) 9,8 + 0 → 𝐻1(𝑞𝑚á𝑥) = 13,8𝑚
𝐻2(𝑞𝑚á𝑥) = 13,8 − 1,253 2∗9,8^2 [0,02 ∗ (^) 0,0508^8 ] − 8,91 2∗9,8^2 [0,02 ∗ (0,7+0,24)0,021 ] − (^) 2∗9,83,8^2 [0,02 ∗ (^) 0,02920,095]
𝐻2 = 9,87m
𝐻2(𝑞𝑚á𝑥) = 3,8 2∗𝑔^2 + 𝑃(𝑞𝑚á𝑥)9,8 + 0 → 𝑃(𝑞𝑚á𝑥) = 89,5𝑘𝑃𝑎
Para as outras vazões: H1(q2) = 15,77m → 𝐻2(𝑞2) = 13,31 → 𝑃(𝑞2) = 122,6𝑘𝑃𝑎 H1(q1) = 21,52m → 𝐻2(𝑞1) = 20,23 𝑃(𝑞1) = 194,2𝑘𝑃𝑎
Para a vazão máxima 𝐹𝑥(𝑞𝑚á𝑥) = −[89400 ∗ 𝜋(12,5 ∗ 10−3)^2 ∗ (−1) + 0 + 0,00254 ∗ 1000(0 − 3,8) + 0)] →
𝐹𝑥 = 53,5N
Para as outras vazões 𝐹𝑥(𝑞2) = −[122600 ∗ 𝜋(12,5 ∗ 10−3)^2 ∗ (−1) + 0 + 0,00201 ∗ 1000(0 − 3,967) + 0)] →
𝐹𝑥 = 68,1N
𝐹𝑥(𝑞1) = −[194200 ∗ 𝜋(12,5 ∗ 10−3)^2 ∗ (−1) + 0 + 0,00145 ∗ 1000(0 − 2,86) + 0)] →
𝐹𝑥 = 99,5N
Área do tubo 𝐴𝑡𝑢𝑏𝑜 = (32^2 − 29,2²) ∗ 𝜋)/4 = = 135𝑚𝑚²
Equação da Quantidade de Movimento 𝐹𝑠 = −(𝑝1𝐴1𝑛1 + 𝑝2𝐴2𝑛2 + 𝑄𝑚 ∗ (𝑣2 − 𝑣1)) 𝑝2 = 0 (𝑟𝑒𝑙) 𝑒 𝑣1 = 𝑣2 , logo: 𝐹𝑠 = −(𝑝1𝐴1𝑛1) = −𝑝1𝐴1𝑛1 ∗ (−1) 𝐹𝑠 = 𝑝1𝐴1𝑛 𝐹𝑠𝑥 = 𝐹𝑠𝑦 = 𝑝1𝐴1𝑐𝑜𝑠𝜃 Ou 𝐹𝑠𝑥 = 𝑝1 ∗ 𝐴𝑐𝑜𝑡𝑜𝑣𝑒𝑙𝑜 ∗ 𝑐𝑜𝑠45º