Pré-visualização parcial do texto
Baixe Capítulo 2 Circuitos polifásicos e outras Manuais, Projetos, Pesquisas em PDF para Engenharia Elétrica, somente na Docsity!
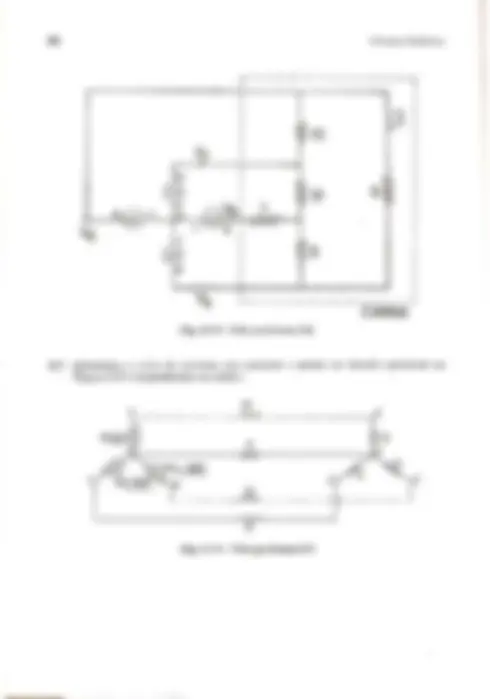
CAPÍTULO 2 Circuitos Polifásicos Sistema polifásico é aquele constituído por duas ou mais tensões. Sua utilização mais comum ocorre na geração e na transmissão de energia elétrica, através do sistema trifásico. Outras formas, como sistemas hexafásicos e dodecafásicos, são bastante encontradas em aplicações que envolvem obtenção de tensões retificadas. Na área de transporte de energia estuda-se a viabilidade de conversão de circuitos duplos trifásicos em circuitos hexafásicos. A quase totalidade dos geradores modernos é trifásica. Três fases são igualmente preferidas quando se trata de transmitir grandes quantidades de potência. De modo geral, equipamentos e aparelhos trifásicos são mais eficientes que os monofásicos. Esses fatores justificam a atenção especial que neste capítulo será dada aos sistemas trifásicos. 2.1 - Definições Define-se como sistema de tensão polifásico equilibrado e simétrico a n fases, um sistema do tipo: vi = Va senmt vo = Va seno t+ 1.25) 27 vs = Vasen(mt+2. (2.1) Un Vn sen [ot +(n-1).23) onde n é um número inteiro qualquer, não menor que 3. Observe-se que o conceito de equilíbrio tem, aqui, idéia de simetria. Não será equilibrado, do ponto de vista elétrico, o sistema cuja soma das tensões seja nula; é necessário, ainda, que tais tensões sejam defasadas entre si pelo mesmo ângulo, o que implica em certa simetria. No caso particular de um sistema trifásico tem-se n = 3 e portanto: vi = Vasenmt 42 Circuitos Polifásicos Vm sen (w t + o) va = (2.2) vs = Va sen (+58) f fasorial d. v=tE, ou, na forma fasorial, sendo V ==: Vi =V/0 Vo = V/27/3 Vs = V/4m/3 v LINHA DE REFERÊNCIA v V3 Va 0 T am w (a) (b) Fig. 2.1 - Tensões trifásicas: a) variando no tempo; b) representação fasorial. A Figura 2.1 mostra a variação, no tempo, das tensões integrantes da Equação 2.2 e a Figura 2.1.b apresenta sua representação fasorial. 2.2 - Obtenção de Sistemas Polifásicos Considere-se o alternador elementar polifásico, mostrado na Figura 2.2. Trata- se, mais precisamente, de um gerador de c.a. trifásico, servindo bem para mostrar como são geradas tensões polifásicas. As bobinas a , b , c , de terminais identificados por aa”, bb”, cc”, são supostas idênticas, de N espiras cada uma, e estão dispostas no estator defasadas entre si de 120 graus. O rotor é constituído por um ímã ou por bobinas excitadas por corrente contínua. O rotor proporciona fluxo constante O e gira à veloci- dade angular constante q. Em cada instante a posição do rotor pode ser definida pelo 44 Circuitos Polifásicos Observa-se, na Figura 2.2, que as tensões passam por seus máximos na seguinte ordem: a, c, b. Portanto, a seqiiência de fases é, no caso, a,c,b (ou c,b,a; ou ainda b,a,c, que estão no mesmo sentido de giro). Caso ocorresse uma inversão do sentido de rotação do alternador mostrado na Figura 2.2, ter-se-ija inversão da sequência de fases, que passaria a ser q, b, c (ou b,c,a; ou ainda c,a,b). É comum chamar-se a sequência a,b,c de segiência direta ou segiência positiva; e a,c,b é usualmente chamada de segiiência inversa ou segiúência negativa. Para inverter a seqiiência de fases de um sistema trifásico, basta trocar entre si as posições de duas fases quaisquer. O sentido de rotação dos motores de indução trifásicos depende da segiiência de fases das tensões aplicadas. Ao se inverter a sequência de fases das tensões aplicadas, inverte-se o sentido do campo magnético girante e, em consequência, inverte-se o sentido de rotação do motor. ' Nos sistemas trifásicos equilibrados, a inversão da segiência de fases modifica os ângulos de fase das tensões e das correntes mas não altera seus módulos. Nos sistemas trifásicos desequilibrados, a inversão da segiência de fases modifica o módulo eos ângulos de fase das tensões e correntes em jogo. Exemplo 2.1 Um sistema trifásico simétrico apresenta sequência de fases inversa e sabe-se que V. = 100 /60º. Determine as tensões Va, Vb. Solução A sequência de fases dada é a,c,b. Então: Vo = 100 /60º — 120º = 100 /- 60º = 100 /60º + 120º = 100 /180º 2.4 - Operadores de Rotação de Fase Na definição de sistemas polifásicos observa-se existir uma diferença de fase de 2Z radianos entre as grandezas que os caracterizam. Objetivando facilitar os cálculos, procura-se definir um operador que provoque tal rotação quando aplicado a um fasor. É o operador p , definido por: p=1/27/n=1/360º/n (2.6) No caso específico de sistemas trifásicos (n = 3), adota-se o operador a=1/120º, que aplicado a um fasor qualquer faz com que ele seja adiantado de 120 graus. Assim: d*=1/240=1/-120"= d=d.a=1/0º Circuitos Polifásicos a?=1/-240º=1/120º=a 1+a+a=0 Exemplo 2.2 Obtenha o valor de 1 — o. Solução 8, 2 1-9=1-1/240º=1-(-5-j mol Exemplo 2.3 Obtenha o valor de d-a. Solução d-act-d=a(-a)=a.V3./30º=vV3/-90º 2.5 - Tensões e Correntes em Circuitos Polifásicos Equilibrados 45 Sejam duas redes A e B, interligadas por n + 1 condutores, conforme mostra a Figura 2.3. Um dos condutores, o mais inferior no desenho, servirá de ponto de referên- cia para tensões; é denominado neutro e identificado pela letra n. Os demais condutores são chamados fases e recebem letras individuais para caracterizá-los. Fase a la. Rede A | Fase b Tb, Rede B ! 1 j- - ; Van |Vbn ' | . FASE Y —lw NEUTRO Yen —lIn ATIVA PASSIVA Fig. 2.3 - Redes polifásicas interligadas por n+1 condutores. Tendo por base a Figura 2.3, define-se como: — tensão de fase (ou tensão fase-neutro) Vf - a tensão existente entre qualquer condutor fase e o neutro (exemplo: V = Van); — tensão de linha (ou tensão fase-fase) Vj - a tensão existente entre duas fases quaisquer (exemplo: V; = Vab); Circuitos Polifásicos 47 O cálculo das tensões de linha (ou tensões fase-fase) pode ser efetuado com a aplicação da Lei de Kirchhoff das tensões (ainda Figura 2.3): Vij= Vin — Vjn = Vi Lay- Vjloy (2.11) Tratando-se de sistema polifásico de tensão com mesma amplitude, tem-se: Vi=V=V; ea Equação 2.11 torna-se: Vij= Vi Log- 1/0) = (2.12) =Vpl(cos a; - cosa; +j (sen a; - sena;)] Caleculando-se o módulo de V;; obtido pela igualdade 2.12 e introduzindo-se as identidades trigonométricas cos? A +sen?A=1 cos (A-B)=cosA.cosB+senA .senB chega-se a: Vij= [Vis] = Vpv2- 2 cos (o; - 09) E então: Viy= | Vis] = Vpv2Ti = costa; a] (2.13) Exemplo 2.4 Determine o módulo das tensões de linha de um sistema trifásico equili- brado cujo módulo da tensão de fase é Ve cuja sequência de fases é a, b, c. Solução " Para n = 3 tem-se: a; - q;= a = 120º. Portanto: Viy= VpvZTI= cos (o; = 09] = Vpv2 (= cos 120º) = 3 V; Exemplo 2.5 Na Figura 2.4 está representado o diagrama fasorial das tensões de fase de um tema hexafásico. O módulo da tensão de fase é V. Determine os módulos das tensões linha entre a fase a e cada uma das fases restantes. 48 Circuitos Polifásicos Solução 7 1 Was|=VV2a-D=V [Mel=vV2a+D=vãvo Va Va [Vaa |=VVZd+D=2V [Vie [= [Vac Yo vp Fig. 2.4 - Sistema hexafásico (Vide exemplo 2.5). 2.6 - Fator de Potência de Circuitos Polifásicos Equilibrados Por definição, o fator de potência de um sistema polifásico equilibrado é o co-seno do ângulo entre tensão de fase e corrente de fase, qualquer que seja o tipo de ligação da carga. Supondo-se que o sistema polifásico apresentado na Figura 2.3 equilibrado e simétrico, tenha V, n como referência e sequência de fases direta (a, b, e, «.., Y). Pode-se então escrever: Van = Von =... = Vn = Vy e mais: qq =0 aq =-0 q=-20 q=-(n-1)0 De modo análogo, para as correntes de fase: Lh=h= -=L= 1 e mais: doa=dp= 0 =... =dy = Oa-Pa onde o fator de potência do sistema é cos da. 50 Circisitos Polifásicos Y Pare Vinde cos da (2.18) Riva Y Que = 3 Vkn- Ih. sen qr (2.19) =a 2.8 - Ligação de Impedâncias em Circuitos Polifásicos Equilibrados Considere-se uma vez mais a Figura 2.3, onde a rede B é passiva e composta por n elementos de igual impedância. Esses elementos só podem sér interconectados de duas maneiras diferentes, de modo a manter o equilíbrio do sistema: conexão em estrela e conexão em malha. 2.8.1 - Conexão em Estrela A conexão em estrela, mostrada na Figura 2.6, caracteriza-se pela existência de um ponto comum de ligação de todas as impedâncias e alimentação da rede nas outras extremidades. g ly — É E po Ty — É T+ e ly — A + x ly — oo N [1 "o na Ea T+ Fig. 2.6 - Conexão em Estrela. Fig. 2.7 - Diagrama fasorial da conexão em Estrela. Adotando-se V, n como referência (diagrama fasorial da Figura 2.7), as tensões de fase são expressas por: Van = VIC, Von = Vi-O,..., Vyn = Vi-(n-DO As correntes Tay, IJby, -..» 1yy têm o mesmo módulo e diferem no ângulo de fase. Como o sistema é equilibrado, pode-se escrever: ly+hby+...+hy=-Ten=0 Circuitos Polifásicos 51 Portanto, nenhuma corrente flui pelo neutro nºn, o que significa que eletrica- mente os pontos n e nº coincidem. A corrente 1 y pode ser calculada como: (2.20) Exemplo 2.6 A tensão de fase de um sistema dodecafásico (12 fases) equilibrado, sequência de fases direta, conectado em estrela, tem módulo igual a 50 V. Qual é o valor da tensão de linha entre duas fases adjacentes do sistema em apreço? Solução o. seo 0º -49 * ab = Van — Vbn=50/0º-50/-30º = = 50,0 - 43,3 +) 25,0 = 6,7 + 25,0 [Vas] =258V Exemplo 2.7 Certa carga hexafásica (6 fases) equilibrada, sequência de fases a-b-c-d-e-f, ligação estrela, solicita 1.200 KVA a uma fonte cuja tensão de fase é igual a 1.000 V. O fator de potência da carga é iguala 0,9, atrasado. Pede-se: a) a corrente em cada linha; b) a tensão fase-fase Va e. Solução a) a intensidade da corrente em cada linha será: Sos 1.200.000 6 6 Jaz Va 1000 — 20 A O ângulo da corrente é determinado pelo fator de potência da carga (indutiva). Tem-se: arc cos 0,9 = 25,84º (atrasado). Então: 1, =200/-25,84º A. b) Vae = Va — Ve = 1.000 /0º - 1.000 /- 240º = 1.732 /- 30º Circuitos Polifásicos 5 Afinal: La = 27 (1 - coso) (2.24) A Para a conexão estrela ser equivalente à conexão em malha é necessário que 1, y=Ts. Portanto, igualando-se as expressões 2.20 e 2.24, tem-se: 4 v Z * 27, (1-0 8) e por fim: Za = 2(1-cos0)Zy . (2.25) A Equação 2.25 é utilizada para se efetuar a conversão de circuito ligado em estrela para circuito ligado em malha, e vice-versa. Na situação particular de um circuito trifásico, em que 6 = 120º, ter-se-á: Za = 8Zy (2.26) Exemplo 2.8 Em um sistema hexafásico equilibrado, ligação em malha, seqiência de fases direta, as correntes de fase têm módulo igual a 100 A. Determine o módulo das correntes de linha no sistema, adotando como referência a corrente de fase T, Solução — 860º 6 8 = 60º 1, = is-1ja = 100/0º - 100 /- 300º = 100 /- 60º Portanto, o módulo das correntes de linha é iguala 100 A. Exemplo 2.9 Certa fonte hexafásica equilibrada tem sequência de fases a-b-c-d-e-f e tensão de fase igual a 500 V. Ela fornece 720 kVA a uma carga equilibra- da cujo fator de potência é 0,866 atrasado. Obtenha: a) a corrente de linha; b) a impedância equivalente em estrela; c) a impedância equivalente em malha. Solução a) a corrente da linha a terá para módulo: 720 6 = 0,24hA = 240 500 240 A [| 54 Circuitos Polifásicos Seu ângulo: are cos 0,866 = 30º. Então: T,=240/-30º A. b) a impedância equivalente em estrela é calculada por: c) a impedância equivalente em malha é obtida por: Zn=22Zy(1-cos60)=2.2,08/30º. (1 - cos 60º) = 2,08 /30º 2.9 - Sistemas Trifásicos Equilibrados A quase totalidade da energia elétrica utilizada no mundo é gerada e transmi- tida por intermédio de sistemas de tensões trifásicos equilibrados. Dentre todos os sistemas polifásicos, em igualdade de condições, o trifásico é o mais econômico no que se refere à quantidade de material condutor necessária à trans- missão de energia elétrica. Para o mesmo tamanho, geradores e motores trifásicos possibilitam a obtenção de potências maiores que os monofásicos. Sob regime perma- nente, em circuitos equilibrados, o valor instantâneo da potência trifásica é constante, ao passo que nos circuitos monofásicos a potência instantânea é pulsante, Sistemas trifásicos possibilitam oferecer dois valores distintos de tensões ao usuário (fase-fase e fase-neutro), sendo portanto mais versáteis que os monofásicos. Motores trifásicos geralmente partem sozinhos, sem necessidade de dispositivos adicionais; os monofásicos (exceto os de coletor) não têm partida própria. A geração de tensões trifásicas foi abordada anteriormente neste capítulo, no item 2.2. Geradores de corrente alternada trifásicos são fabricados com potências que variam de 100 kW a 1.300 MW, para operação em tensões que vão de 480 V a 25 kV. Nos sistemas trifásicos podem ocorrer dois tipos de ligações: ligação em estrela ligação em triângulo (ou delta) Note-se que estrela e malha são termos gerais, aplicáveis a sistemas com qualquer número de fases. Todavia, estrela e triângulo (ou delta) são termos específicos para sistemas trifásicos. 2.9.1 - Ligação em Estrela Considere-se a ligação em estrela mostrada na Figura 2.9. Se o sistema apre- senta tensões de alimentação equilibradas, com seqiiência de fases direta (a, b, c), pode-se escrever para as tensões de fase: Va=V/00 Vo=V/-120º Vo=V/120º 56 Circuitos Polifásicos equivalente e se aplica somente a sistemas equilibrados. As ten- sões e correntes nas outras fases são obtidas a partir do circuito monofásico equivalente, atra- vés da rotação de + 120º e le- vando-se em conta a sequência de fases. O diagrama fasorial correspondente às tensões e cor- rentes na ligação em estrela é mostrado na Figura 2.11. Fig. 2.11 - Diagrama fasorial para um sistema tri- fásico em estrela. Exemplo 2.10 Certa carga equilibrada ligada em estrela é suprida por um sistema trifásico simétrico com seqiiência de fases direta. Sendo Vj, = 100 /60º V, determine: a) as tensões de fase; b) as tensões de linha. Solução a) Tendo em vista a sequência | de fases estabelecida, os máximos de tensão ocorrem na seguinte ordem: Vs, V., Va Portanto: Vo = 100 /60º V V. = a? V, = 100 [60º - 120º = 100/-60º V Va=a Vo = 100 /60º + 120º = 100/180º V b) As tensões de linha são: Vab = Va — Vo =— 100 — 100 [60º = 3 100 /210º V Vbe = Vo - V. = 100 /60º - 100 /-60º = 3 100 /90º V Vea = Ve- Va =100/-60º - 100=vV3 100/-30ºV Circuitos Polifásicos 57 Exemplo 2.11 Resolva o exemplo anterior supondo agora segiiência de fases inversa. Solução a) Para a segiiência de fases inversa a ordem dos máximos das tensões passa a ser: Vs, Va, Ve. Então, as tensões de fase assumem os seguintes valores: » = 100 /60º volts = 2 V = 100 /60º - 120º = 100 /- 60º volts Ve = a Vy = 100/60º + 120º = 100/180º volts 6) Para as tensões de linha pode-se escrever: Vas = Va-Vb = 100/-60º - 100/60º = 3 100/-90ºV be = Vb-V. = 100/60º - 100/180º = 3 100 /30ºV Voa = Ve-V. = 100/180º- 100 /- 60º = v3 100 /150V 2.9.2 - Ligação em Triângulo (ou Ligação em Delta) Conforme mostra a Figura 2.12, a ligação em triângulo apresenta tensões de linha iguais às tensões de fase. Por outro lado, as correntes de linha T, 1», I., são diferentes das correntes de fase 1, b, Ip c, le a (correntes que circulam nas impedâncias da carga). Admitindo que a segiiência de fases seja Va = Vi/Oº, Voc = Vp/- 120º, Voa = Vp/120º a —» lg e Ica o o [= ion | ] Fig. 2.12 - Ligação trifásica em triângulo. Csrcuitos Polifásicos 59 Exemplo 2.12 Uma carga equilibrada ligada em triângulo apresenta em cada lado uma resistência de 12 ohms em série com uma reatância capacitiva de 16 ohms. Tensões de linha equilibradas de 115 V são aplicadas à carga, em sequência de fases direta. Determine os módulos das correntes de fase e das correntes de linha. Solução A impedância de cada lado do triângulo é 12 - ; 16 e tem módulo igual a 20 Q. Portanto: 115 [== 5,154 [E =v3 [77] =V3.5,15= 9,954 2.9.3 - Associação de Cargas Trifásicas Equilibradas, em Paralelo A composição de várias cargas trifásicas equilibradas em paralelo pode ser efetuada da maneira seguinte: elege-se um tipo de ligação (estrela ou triângulo), transforma-se todas as cargas para o tipo eleito, e a seguir, pela aplicação da lei que overna circuitos em paralelo, chega-se à impedância final. Recai-se, então, num dos casos já vistos. Pode-se, ainda, trabalhar com os valores das potências das várias cargas, somando-se aritmeticamente as potências ativas e algebricamente as potências reativas; a potência aparente total será obtida por s=VP?+ q? Por convenção, considera-se positiva a potência reativa de circuitos indutivos negativa a potência reativa de circuitos capacitivos (convenção do American Institute letrical Engineers (A.LE.E.)). Exemplo 2.13 Cada lado de uma carga equilibrada conectada em triângulo tem 6 ohms de resistência e 9 ohms de reatância capacitiva, em série. Cada parte de uma carga equilibrada ligada em estrela apresenta 8 ohms de resistên- cia e 6 ohms de reatância indutiva, em série. As duas cargas são ligadas em paralelo através de tensões de linha trifásicas de 100 V. Calcule a corrente de linha resultante. Solução Transformando o triângulo em estrela, conforme expressão 2.26, cada perna á a impedância igual a: 6-j;9 mv A estrela final equivalente terá, por fase, a impedância resultante da associa- em paralelo de 2 —j 3 com 8 + 6, cujo módulo é igual a 3,45 Q. Portanto: 100 v3 [il -sãg" 1674 60 Circuitos Polifásicos 2.9.4 - Resolução de Circuitos com Gerador e Carga Ligados em Estrela No circuito trifásico da Figura 2.14 estão representados um gerador ligado em estrela, uma carga ligada em estrela, e uma linha de transmissão que interliga o gerador ea carga citados. vLoe Zg | 1 Z | 1 Z QE ds —la Fm 1 —m ev) | + | vi-po 7 | z Z 7 - Llb-b It . , n + 1 7 o, I LI | | 5 I vir 120º z rá oz “é ELlc-t À (Gerador Y) | (Linha) ! (Carga Y) | I [E | (FIO NEUTRO) Fig. 2.14 - Gerador e carga ligados em estrela. Como o sistema é suposto equilibrado, as tensões nos pontos n e nº são iguais e a soma das correntes 1., 1, 1. é nula. Conclui-se daí que T, = 1, + Ty + 1. = 0. O circuito dado pode então ser reduzido ao monofásico equivalente mostrado na Figura 2.15, tendo a fase a como referência. = z , a — la a uu a ue À + — — = vi t n n Fig. 2.15 - Circuito monofásico equivalente. A corrente na fase a é calculada por: V/ 0º =5—5—s 2.36, * Z+M+Z (2.86) E nas demais fases, por: Lb=d1, (2.37) T.-al