Cálculo Vetorial e Geometria Analítica Espacial
Professor Hans
Aula 1: Elipse - Teoria
Cônicas
As cônicas – hipérbole, parábola e a elipse possuem
todas elas, um aspecto singular: podem ser obtidas através
da interseção de um plano convenientemente escolhido
com uma superfície cônica, conforme mostrado na figura a
seguir:
Uma seção cônica é uma curva cuja equação cartesiana
é do segundo grau, e inversamente, toda curva cuja
equação é do segundo grau pode ser obtida a partir da
interseção de um cone circular reto de duas folhas com um
plano. Por essa razão, as curvas cujas equações são do
segundo grau são chamadas de seções cônicas, ou
simplesmente de cônicas.
Elipse
A Elipse é o lugar geométrico dos pontos P do plano
cuja soma das distâncias a dois pontos fixos, 1
F
e 2
F
,
situados no mesmo plano, é constante e igual ao eixo
maior.
Equação Natural da Elipse
122
P
FPF+=
uuur uuur a
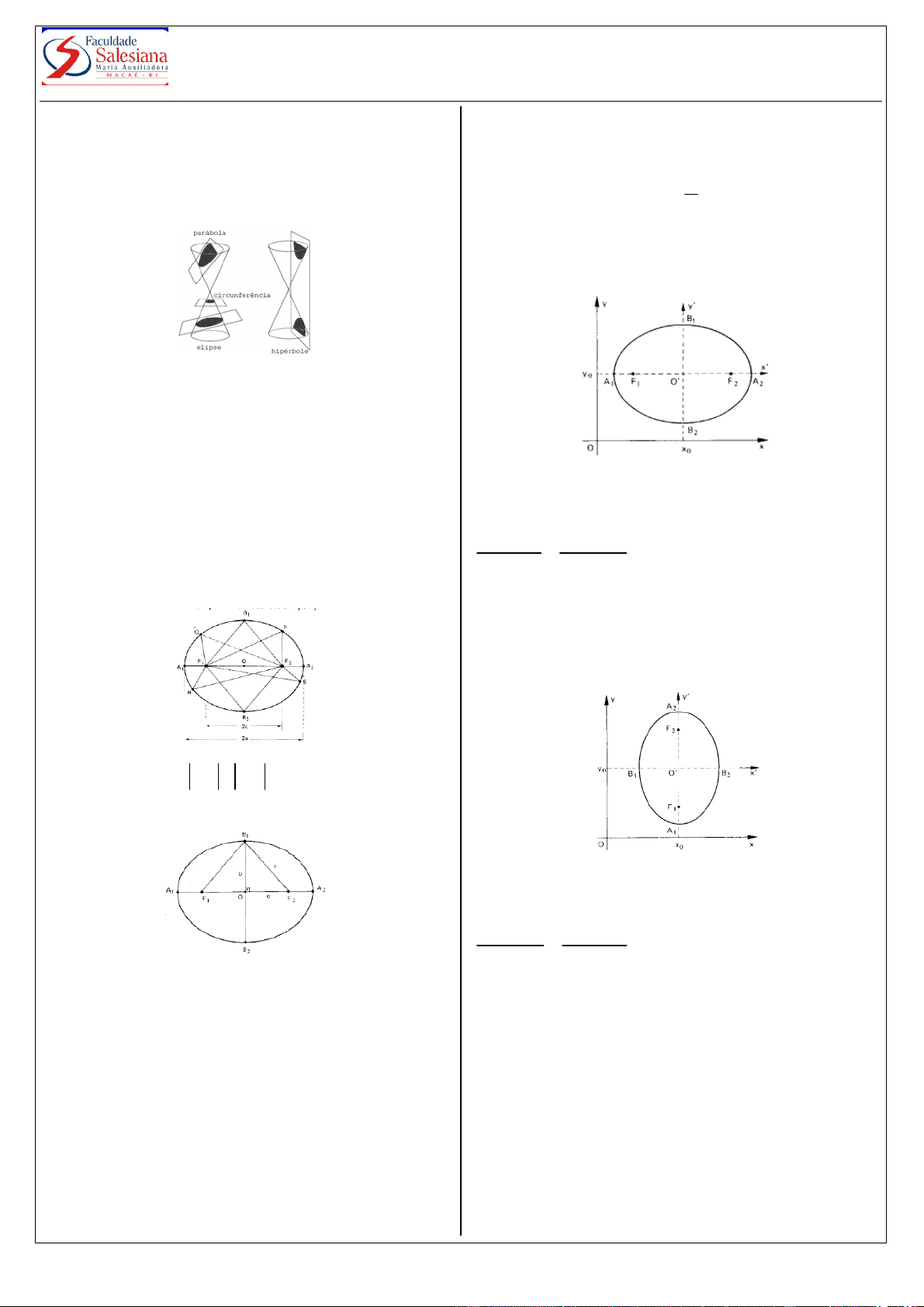
Elementos Principais
O - centro da elipse
1
F
e 2
F
- focos da elipse
1
A
,2
A
,1
B
, 2
B
- vértices da elipse
12 2
A
A=a
- eixo maior
12 2
B
B=b
- eixo menor
12OA OA a==
- semi-eixo maior
12OB OB b==
- semi-eixo menor
12 2
F
F=c
²
Excentricidade
É a razão entre 2c) e o eixo maior
(2a)
- distância focal
12OF OF c==
- semi-eixo focal
Relação Fundamental
²²abc=+
a distância focal (
. c
ea
=
Obs. Na elipse teremos 0 < e < 1
lipse
Eixo Maior Para sas
.
Equações da E
lelo ao Eixo das Abscis
Focos
0)0(;
F
xcy
±
Equação Cartesiana
00()²( )²xx yy 1
²²ab
−
−
+
=
Equação Paramétrica
0cosxxa
0
yybsen
θ
θ
=+
⎧com 02
⎨=+
⎩
θ
π
≤
≤
ixo Maior Paralelo ao Eixo das Ordenadas E
Focos
0(;0)
F
xy c
±
Equação Cartesiana
00()²()²yy xx 1
²²ab
−
−
+
=
Equação Paramétrica
0cosxxb
0
yyasen
θ
θ
=+
⎧ com
⎨=+
⎩02
θ
π
≤≤
Aplicações da Elipse
*A reta tangente a P forma ângulos uma elipse em um ponto
iguais com os raios focais (segmento de reta 1
F
P e 2
F
P).
Assim, se um raio de luz passa pelo foco de elip se
reflete no ponto P, então ele também passa pelo outro foco. Essa
propriedade é chamada propriedade óptica das elipses.
* De acordo com o modelo de Sommerfeld, num átomo, os
uma se e
elétrons descrevem órbitas elípticas em torno do núcleo.
* Kepler mostrou que a trajetória dos planetas ao redor do Sol
tem forma de uma elipse.