Cálculo Vetorial e Geometria Analítica Espacial
Professor Hans
Aula 1: Elipse - Exercícios
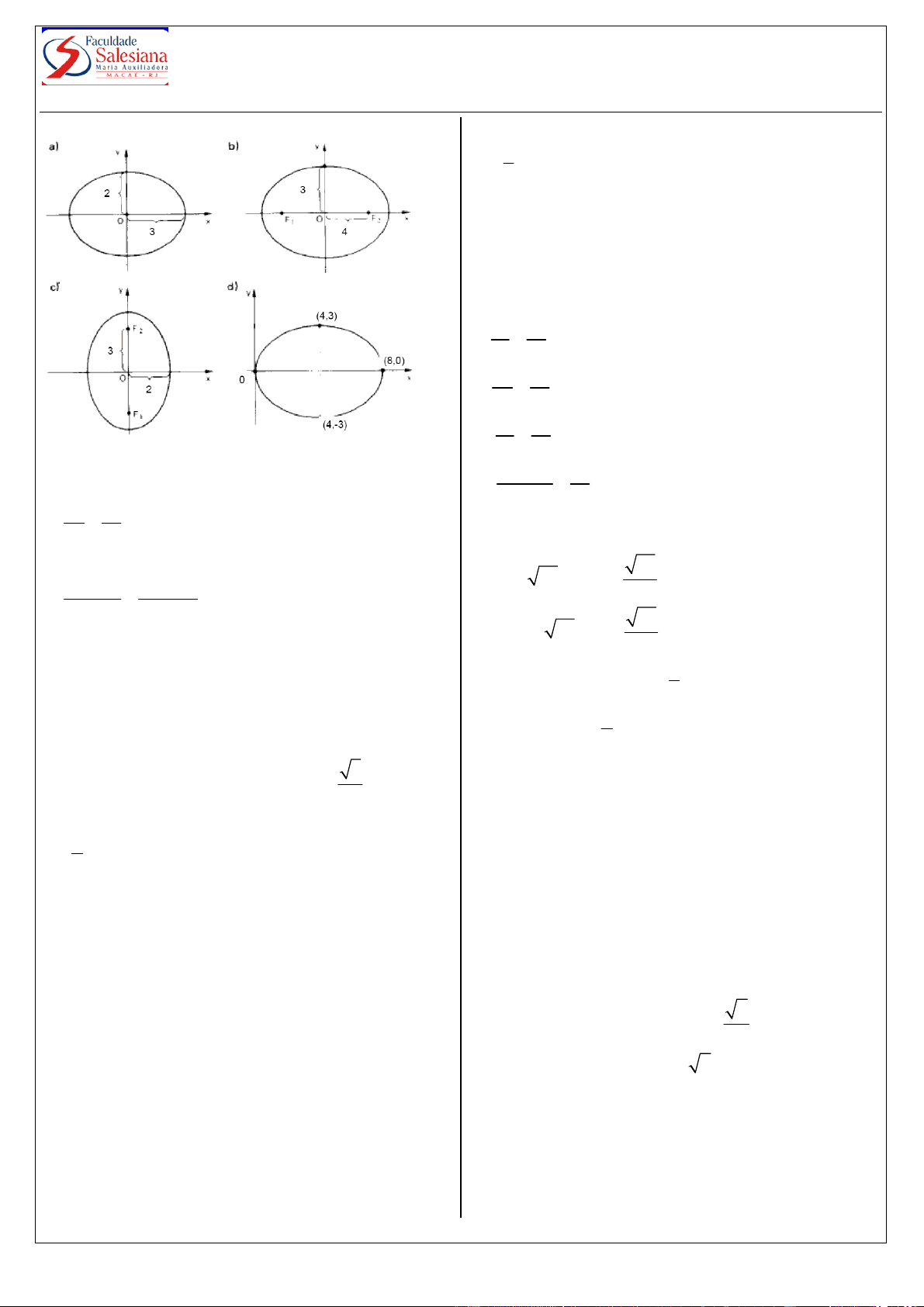
1) Determinar as equações das elipses seguintes:
2) Determine os focos, a excentricidade e esboce os
gráficos das elipses:
a) ²²
1
25 4
xy
+=
b) 25 ² 4 ² 100xy+=
c) 22
(5)( 2)1
25 16
xy−−
+=
d) 9 ² 5 ² 45 0
xy+−=
3) Determine uma equação da elipse que satisfaça a
condição dada.
a) Focos: (-4, 0) e (4, 0), eixo maior igual a 10.
b) Focos: (0, -5) e (0, 5), eixo menor igual a 10.
c) Focos: ( , e excentricidade 0, 3)
±3
2
e=.
d) Centro: C(1, 4), um foco F(5, 4) e excentricidade
2
3
e=
4) Obtenha as equações paramétricas das elipses:
a)
²4²4xy+=
b)
²²3xy+=6
c) 9(
1)² 25( 1)² 225xy−+ +=
d) 49(
7)² ² 7xy++=
5) Determinar uma equação geral da elipse dada por
equações paramétricas.
a) 5cos
5
x
y
sen
θ
θ
=
⎧
⎨=
⎩
b) 24cos
32
x
y
sen
θ
θ
=+
⎧
⎨=+
⎩
6) Um satélite de órbita elíptica e excentricidade
1
3
e
=
viaja ao redor de um planeta situado num dos
focos da elipse. Sabendo que a distância mais próxima
do satélite ao planeta é de 300km, calcule a maior
distância.
Gabarito
1)
a) ²²
1
94
xy
+
=
b) ²²
1
25 9
xy
+
=
c) ²²
1
413
xy
+
=
d) (4)² ²
1
16 9
xy
−
+
=
2)
a) (21,0)F±, 21
5
e=
b) (0, 21)F±, 21
5
e=
c) e ,
(8,2)F'(2, 2)F3
5
e=
d) (0, 2)F
±
, 2
3
e
=
3)
a) 9 ² 25 ² 225xy
+
=
b) 2 ² ² 50xy
+
=
c) 4 ² ² 12xy
+
=
d) 5 ² 9 ² 10 72 31 0xy xy
+
−− −=
4)
a) 2cosx
y
sen
θ
θ
=
⎧
⎨=
⎩ b) 6cos
6
x
y
sen
θ
θ
=
⎧
⎨=
⎩
c) 15cos
13
x
y
sen
θ
θ
=+
⎧
⎨=− +
⎩ d)
7
7cos
7
7
x
ysen
θ
θ
⎧=− +
⎪
⎨
⎪=
⎩
5) a) ² ² 25xy
+
= b) ² 4 ² 4 24 24 0xyxy+−−+=
6) 600 km