























































Estude fácil! Tem muito documento disponível na Docsity

Ganhe pontos ajudando outros esrudantes ou compre um plano Premium


Prepare-se para as provas
Estude fácil! Tem muito documento disponível na Docsity
Prepare-se para as provas com trabalhos de outros alunos como você, aqui na Docsity
Os melhores documentos à venda: Trabalhos de alunos formados
Prepare-se com as videoaulas e exercícios resolvidos criados a partir da grade da sua Universidade
Responda perguntas de provas passadas e avalie sua preparação.

Ganhe pontos para baixar
Ganhe pontos ajudando outros esrudantes ou compre um plano Premium
Comunidade
Peça ajuda à comunidade e tire suas dúvidas relacionadas ao estudo
Descubra as melhores universidades em seu país de acordo com os usuários da Docsity
Guias grátis
Baixe gratuitamente nossos guias de estudo, métodos para diminuir a ansiedade, dicas de TCC preparadas pelos professores da Docsity
apostila pressão hidrostática mecânica dos fluidos exercicio resolvido
Tipologia: Exercícios
1 / 69

Esta página não é visível na pré-visualização
Não perca as partes importantes!






























































Atenção : Estas notas de aula destinam-se exclusivamente a servir como roteiro de estudo. Figuras e tabelas de outras fontes foram reproduzidas estritamente com fins didáticos.
Prof. Lucrécio FÁBIO
Ao concluir esta Unidade você deverá ser capaz de:
Determinar a variaçã o da pressã o em um fluido em repouso; Calcular as forç as exercidas por um fluido em repouso em superfí cies submersas planas ou curvas; Analisar o empuxo
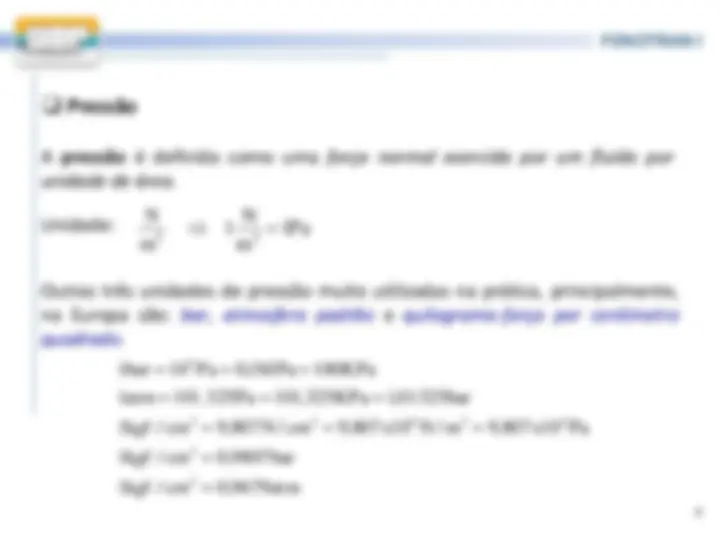
A pressão é definida como uma força normal exercida por um fluido por unidade de área.
Unidade: 2 m
1 Pa m
Outras três unidades de pressão muito utilizadas na prática, principalmente, na Europa são: bar , atmosfera padrão e quilograma-força por centímetro quadrado.
1 kgf /cm 0 , 9679 atm
1 kgf /cm 0 , 9807 bar
1 kgf /cm 9 , 807 N/cm 9 , 807 x 10 N/m 9 , 807 x 10 Pa
1 atm 101. 325 Pa 101 , 325 KPa 1 , 01325 bar
1 bar 10 Pa 0 , 1 M Pa 100 KPa
2
2
2 2 4 2 4
5
Observe que as unidades de pressã o bar, atm e kgf/cm^2 sã o quase equivalentes entre si. No sistema inglê s, a unidade de pressã o é libra-forç a por polegada quadrada (lbf/pol^2 ou psi) e 1 atm = 14 , 696 psi.
As unidades de pressã o kgf/cm^2 e lbf/pol^2 també m sã o indicadas por kg/cm^2 e lb/pol^2 , respectivamente, e normalmente sã o usadas em calibradores de pneus.
A pressã o també m é usada para só lidos como sinô nimo de tensã o normal, que é a forç a que age perpendicularmente à superfí cie por unidade de á rea. Observe a figura ao lado
f^2 2
f pés
n (^300) cm =^0 ,^25 kg /cm
A
P=σ =
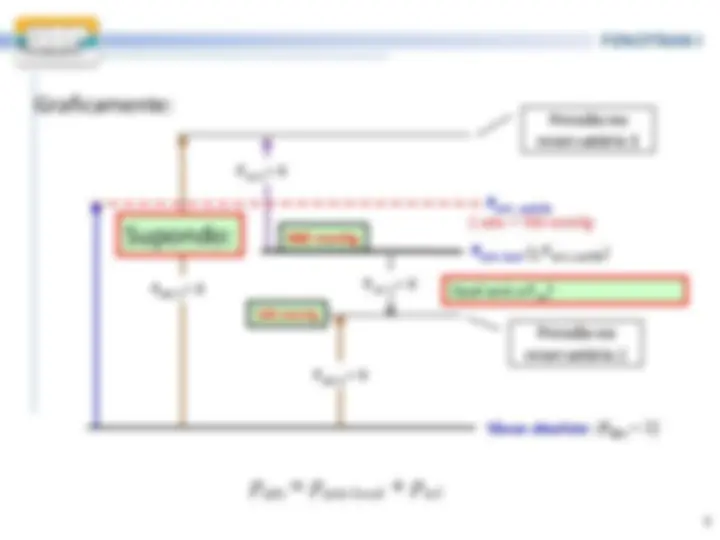
Graficamente:
Patm, local (< Patm, padrão) Pressão barométrica
Patm , padrão (nível do mar) 1 atm = 760 mmHg
Pabs 1 > 0
Prel 1 > 0
Pabs 2 > 0
Prel 2 < 0
Vácuo absoluto (Pabs = 0)
Pressão no reservatório 2
Pressão no reservatório 1
Associação de níveis a pressões para definição de pressão absoluta e pressão relativa (efetiva) pabs = patm local + prel (^) (1)
Graficamente:
Patm, local (< Patm, padrão)
Patm , padrão 1 atm = 760 mmHg
Pabs 1 > 0
Prel 1 > 0
Pabs 2 > 0
Prel 2 < 0
Vácuo absoluto (Pabs = 0)
Pressão no reservatório 2
Pressão no reservatório 1
pabs = patm local + prel
Supondo: 680 mmHg
500 mmHg
Qual será a Prel?
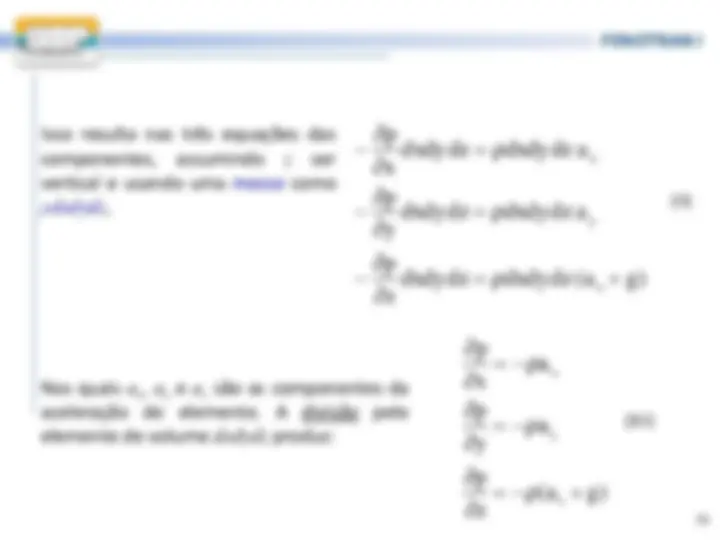
Ao aplicar a segunda lei de Newton ao elemento, para ambas as direções : x e z.
z s sen
x scos
x x x s 2 ax
x y z F ma p z y p s ysen
^ (2)
z z z s 2 az
x y z p s ycos 2
x y z F ma p x y g
^ (3)
a x p (^) x ps x
(4)
(a g) z p (^) z ps z
Qual o significado disso???
Fx m
Analisando a geometria da figura, tem-se:
Substituindo os valores de Δz e Δx nas equações (2) e (3), respectivamente, tem-se:
Note que, no limite em que o elemento diminui até um ponto:
z 0
x 0
O lado direito das equações (3) e (4) vão a zero, mesmo para fluidos em movimento, resultando que, em um ponto,
p (^) x pz ps
Ela age igualmente em todos as direções em um determinado ponto, tanto para um fluido estático como para um fluido em movimento na ausência de tensão de cisalhamento.
Obs.: Como θ é arbitrário, essa relação é valida para todos os ângulos em um ponto. O plano xy também poderia ser analisado e, então, concluiríamos que px = py = pz = ps. Ou seja, a pressão no fluido é constante em um ponto (a pressão é uma função escalar).
Forças agindo em um elemento infinitesimal que está em repouso no referencial xyz
p
dz z
p dy y
p dx x
p dp
^ (6)
Se nos movermos do centro para uma das faces a uma distância afastada de dx/2 , percebemos que a pressão é:
2
dx x
p ,y,z) p(x,y,z) 2
dx p( x
^ (7)
A segunda lei de Newton é escrita na forma vetorial para um sistema de massa constante como:
dp ax dxaydy(az g)dz (11)
dp gdz
dz
dp (12)
Essa equação mostra que não há variação de pressão nas direções x e y , ou seja, no plano horizontal. A pressão varia apenas na direção z.
Nota : dp é negativo se dz positivo, ou seja, a pressão diminui conforme ocorre o movimento para cima e aumenta quando o movimento é para baixo.
Se o ponto de interesse estiver a uma distância h abaixo de uma superfície livre (uma superfície separando um gás de um líquido), como mostrado na figura abaixo, a equação (13) resultará em:
p h (14)
Em que p = 0 em h = 0.
Ponto chave : A equação p = ϒh é usada para converter pressão em altura de um líquido.
Pressão abaixo de uma superfície livre
A pressão de um fluido em repouso não depende da forma ou da seção transversal do contêiner. Ela varia com a distância vertical, mas permanece constante em outras direções (Figura abaixo).
Este princípio foi publicado por Simon Stevin (1548-1620) e ficou conhecido como princípio (lei) de Stevin. (^20)
Pressão em diferentes pontos, abaixo de uma superfície livre
Em h 1 : pa = pb = pc =pd
Em h 2 : pA = pB = pC ≠ pD
ϒH2O ≠ ϒ (^) Hg