







Estude fácil! Tem muito documento disponível na Docsity

Ganhe pontos ajudando outros esrudantes ou compre um plano Premium


Prepare-se para as provas
Estude fácil! Tem muito documento disponível na Docsity
Prepare-se para as provas com trabalhos de outros alunos como você, aqui na Docsity
Os melhores documentos à venda: Trabalhos de alunos formados
Prepare-se com as videoaulas e exercícios resolvidos criados a partir da grade da sua Universidade
Responda perguntas de provas passadas e avalie sua preparação.

Ganhe pontos para baixar
Ganhe pontos ajudando outros esrudantes ou compre um plano Premium
Comunidade
Peça ajuda à comunidade e tire suas dúvidas relacionadas ao estudo
Descubra as melhores universidades em seu país de acordo com os usuários da Docsity
Guias grátis
Baixe gratuitamente nossos guias de estudo, métodos para diminuir a ansiedade, dicas de TCC preparadas pelos professores da Docsity
Arcos e abóbodas
Tipologia: Notas de estudo

Oferta por tempo limitado
Compartilhado em 06/10/2017
4.6
(29)33 documentos
1 / 17

Esta página não é visível na pré-visualização
Não perca as partes importantes!











Em oferta
ARCOS - TRA<;:ADOS DIVERSOS, CONSTRU<;:AO E MATERIAlS. ABOBADAS - TRA<;:ADOS,
CO:\STRU<;:AO, EST ABILIDADE, MATERIAlS, DESCIMBRAMENTO E PES DIREITOS-
40 FIGURAS
DISTRIBUIQAO DA PORTUGALIA EDITORA
LISBOA PREC;0 1$$
ENCICLoptDIA PRATICA
DA CONSTRU~AO CIVIL
,
ARCOS E ABOBADAS
.:0 ah6badas foram nos recuados tempos uns dosmais
:=:-a de cantaria ou em tijolo. As ab6badas cobriram
onstruc;oes, como na arquitectura bisantina, e ser- de tectos como na arte ogival. As ab6badas eram ::::rruidas com mais ou men os importancia, segundo a __- goria do edificio que as comportava. 0;; arcos, de que as ab6badas sao os sellS desenvolvi-
=e os e que datam do tempo das famosas construc;oes
romanas, tern ainda na arquitectura de hoje 0 seu lugar pr6prio, em qualquer dos seus trac;ados. o trac;ado e a constru~ao dos arc os sao urn dos im- portantes estndos a interessar os construtores de qual- quer regiao, pela importancia que actualmente ainda re- vestem. As ab6badas, ja de uso relativamente restrito, sao, porem, tema de certa categoria que os estudiosos nao de- vem alienar. Neste prop6sito damos os desenvolvidos estudos sobre aq ueles arcos que na arquitectura tern mais aplicac;ilO.
I
I . I : / f~,.mel.! / .., <2 L1/'IluuIQnYIfM:·£>l1f'!!. • C" •. , J>/~/7" ekr Iml'.oJ'tor b ....-/-..-:-..-...._..¥-.'-'--"-"-..-.
__ .. 'Imp-orCa" , .. " - ". '1''\ ~~~~~; ;;"~~~;a~,-.
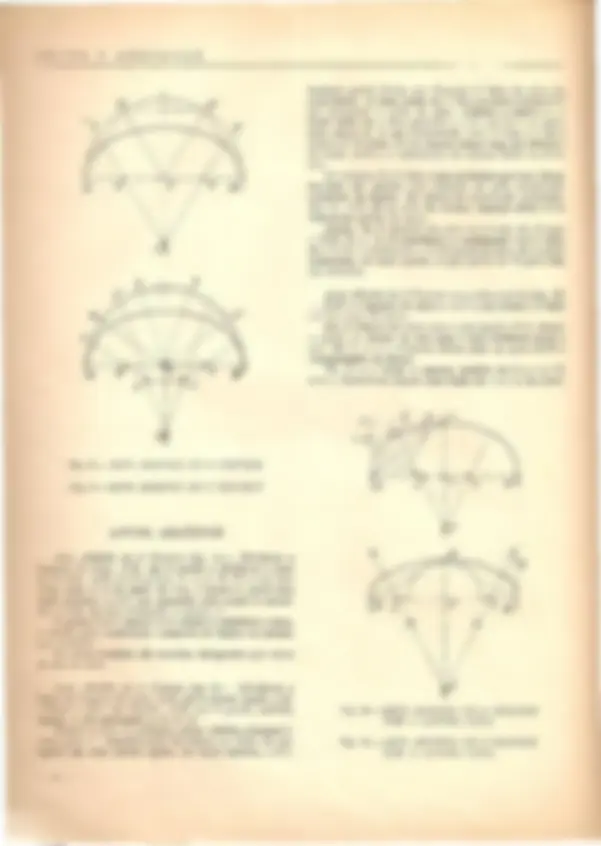
I' pe ,l)/r~/to. .. _ .. _ .. _ .. _ .. _ ... _ .. ...L .. _ .. _ .. _ .. _ .. _ .._ .. : t:t.' : X .N I Fig. 1- GONSTITUIQAO DO ARGO fROMANICO (a-b - largura do arco; cod - raio)
Areo Rom(j,nieo (fig., 3) - Este areo, que e 0 mais " pIes e talvez 0 mais belo de todos os arcos, design a- -~e geralmente por areo de volta perfeita. Constr6j-se achando 0 ponto C, que e 0 eixo da Sua ~cura, na linha A-B. Esta linha e a largura do vao ::de 0 area tern lugar. .."a fig. 1 vemos este arco, com todas as designac;oes :-:'prias da suaconstruC;ao.
i I I II //
. / A'-'-'-'-'fc-'-'---'JJ. I.
, I , '//.:B ---f------¥---, .4 -- '\ (^) , I ,
-----+-----i- " a ,
Ie'
Fig. 3 - ARGO DE VOLTA PERFEITA
Fig. 4 - ARGO AVIAJADO DADO 0 VAO
Areo de Gearr;ao (fig. 2'J-D)- Este areo, tambem conheeido por areo sobrebaixado, e muitas vezes desi- gnado por abatido, embora erradamente. A sua constru- C;ao obtem-se, fazendo 0 seu centro em qualquer ponto da linha do eixo da largura do vao, a b. Este arco I'l, em geral, 0 mais preferido para as res- salvas pela sua construc;ao correntia (i).
Areo de Ferradura (fig. 15)- Obtido 0 ponto C na linha A-B,que e a largura do areo, trac;a-se este, que se prolonga abaixo da referida linha A-B, de ambos os lados, tanto como metade do seu raio. o areo de ferradura, caracterizado na arquitectura arabe, mas de origem n6rdica, nao e mais de que urn areo de volta perfeita ultrapassado.
I ::-t-:.- -- I "-
I I I '. i-- -' .....---....:·~~i·~'---.•.---..-- f i J
I I I , I .. "':->~<" b .::-. +. .:-:_- _ a (^). ' I (^). .b
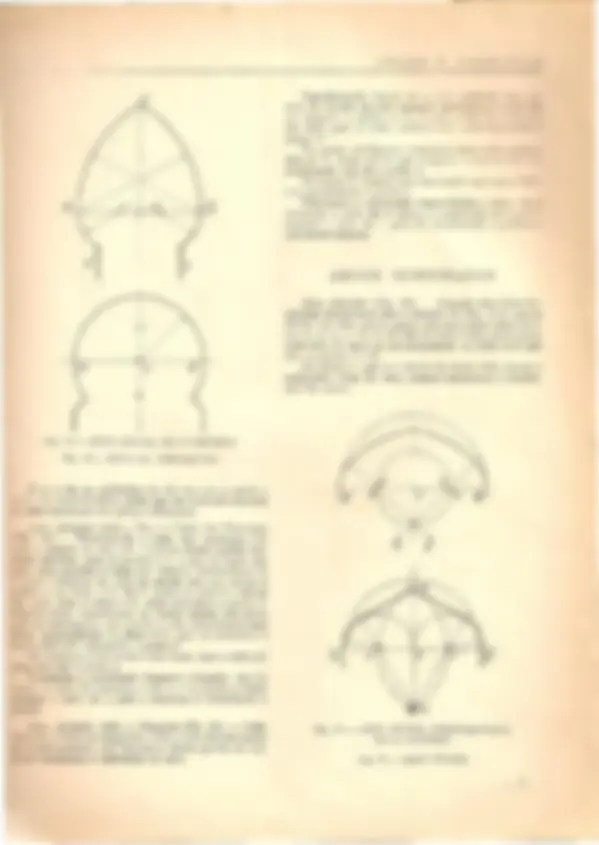
Fig.5-ARGO OGIVAL DE LANGETA
Fig. 6-ARGO OGIVAL Fig. 7-ARG'O OGIVAL SOBREBAIXADO, DE 2 GENTROS DE 3 PONTOS
I a- (^) "... ~~~-_.+"'~ I .." (^) ..•..•.. a' "./ I^ ,'\ -- -- -T--- - "'/-, , I / " b ,~// \ /1 ", hI / I \ .
" II \ 1/ \ " " (^) ,\ _ (^) '1 I'I " f ,^ _^ ~ • _ • -*-. \11^ ...• .. \ f^
:J} 2\ Ie /3 .B " \ II ,/ \ I ' " (^) \ II (^) ,/ \ I '
I~r
A1'CO Abatido de 3 Centros (fig. 8)- Dividese a :l.argura do arco, A-B, em 4 partes e divide·se 0 arco de circulo. A-B, em 3 partes, A, a, a', B, D e a sai uma linha para C e do meio de A-a, 0 ponto b, parte uma linha paralela a a-C, que passando pelo ponto 2 encon- tra a linha de eixo forman do 0 centro 1. o ponto 2 e 0 centro 2 e 0 centro 3 simetrico a esse, e obtido pela constru~ao completa da Figura ou mesmo or simetria. Os arcos abatidos sao tambem designados por areos de asa de cesto.
Areo Abatido de 5 Centros (fig. 9)- Divide-se a a da largura do arco, A-B, em 4 partes iguais e dio e-se 0 arco de circulo, A-B, em 5 partes tambem ais. a que mareamos a, b, b', a'. Destes pontos do poligono assim obtidos, tiramos li- as para C. Seguidamente dividimos os lados do po- 'oono em duas partes iguais, de cujos centros, c ee',
fazemos partir linhas em direeQao it linha do eixo da
ate encontrar a linha do eixo, obtendo 0 centro 1; a
pelo ponto 4. A sua intersec~ao com a linha c'·J da 0 centro 2. 0 centro 4 e ao mesmo tempo uma das divis5es da linha A-B e a intersecQao da mesma linba na linba e-2. Os centros 3 e 5, bem como as linhas que lhes dizem respeito sao obtidas por simetria ou pela construQao completa da figura. As linhas de constru~ao prolonga- das de A-B ate ao arco de eirculo, limitam entre si as diferentes partes do areo. Assim, de 4 tiramos urn area de circulo de A para a linha de c; de 2 centramos a continuaQao ate it linha de c' e de 1 centramos a continuaQao do area ate it parte construida do lado oposto, e que partiu de B para trlis em simetria.
Arco Abatido de 3 Centros com a altura dada (fig. 10)
- A-B e a 11lrgura do areo e A-D a sua altura; a linha
De D tira-se urn area com 0 raio igual aD-A, dando o ponto a, donde se tira para b uma distaneia igual a a-c. De b, a e e tiram-se linbas para A, para melhor compreensao da figura. De D a e da·se a mesma medida de b a a ou de a a c, fazendo·se depois uma linha de cae e da inter-
a --,-ft.- ...::.:--, " ,: " , \ ....I I '........ I ~ ,'~,' I , '. ':', I : - - - L - - - - - ...l- - - - - - 4-.: - 0' .IJ 2.' Ie ,'3 2J '7-" i X . ,
" ,^ \ I • I^ (^) ' I " '. I
~I
Fig. 10-ARCO ABATIDO DE 3 CENTROS COM A ALTURA DADA
Fig. 11- ARCO ABA1'IDO DE 3 CENTROS COM A ALTURA DADA
...• Areo Abatido de 9 Centros (fig. 12). - Divide-se a a da largura do arco, A-B, em 28 partes iguais e a linha do eixo, a partir de C para baixo, divide-se em 4, partes iguais e iguais pOl' sua vez a 4 partes obti- a- na linha A-B. Centrando-se em C tira-se de A para B um arco de c' culo. Seguidamente continua-se a construQao. As di· ,'Boes obtidas na linha do eixo sao: C, a, b, e e 1. Terminadas as divisoes traQam-se as linhas: do ponto 1 da linha do eixo a passar pela divisao 9 da linha A-B, do ponto c a passar pela divisao 6, do ponto b a passar ela divisao 4 e do ponto 4 a passar pela divisao 2. Estas linhas sao prolongadas ate ao arco de circulo, a fim de se limitarem entre elas as diferentes partes da eonstruQao do areo.. Os eentros para a construQao do arco sao: 0 numero '" obtido na intersecQao da linha que vindo de a passa em 2, 0 6 na intersecQao da recta a-2 com a linha b-4, o 4 na intersecQao da recta b-4 com e-6, 0 numero 2 na intersecQao da linha e-6 com 1-9 e finalmente 0 nfunero 1, 0 pr6prio numero 1.
Os centros 3, 5, 7 e 9 obtem-se pOI' simetria.
A1"eo Abatido de 11 Centros (fig. 13). - Divide-se a largura do arco, A-B, em 41 partes iguais e a linha do eixo, a partir de C para baixo, divide-se em 5 par- es. iguais cada uma a um certo numero das partes obtidas na linha A-B. Estas partes na linha de eixo, que SaD C, a, b, e, del, medem no exemplo exposto 9 artes extraidas da linha A-B. Obtida esta construQao, traQam-se linhas que par- :indo dos pontos da linha de eixo vao cruzar-se com as divisoes da linha da largura A-B e se prolongam a"e ao arco de circulo que limitou entre si as diferentes ~ontos do arco A-B. AssilL, partindo uma linha do
. onto 1 cruza a divisao 16, uma do ponto d cruza a dinsao 12, uma do ponto e cruz a a divisao 9, uma do ponto b cruza a divisao 7 e uma do ponto a cruza a insao 6. Os centros para a construQao do arco sao: 0 numero 0, cruzamento da linha a-6 com a linha A·B; 0 8, crllzamento das linhas a-6 com b-7; 0 6, cruzamento das Unhas b-7 com e-9; 0 4, cruzamento das linhas e-9 com ·12; 0 2, cruzamento das linhas d-12 com 1-16, e final- .LL:ente ole 0 pr6prio pontot. Os centros 3, 5, 7, 9 e 11 sao, como se compreende, tirados pOI' simetria.
Areo Ogival de Laneeta (fig. 5). - Divide-se alar- gura do arco, a-b, em tres partes iguais e estabelece-se o prolongamento da recta a-b, mais uma dessas partes ~ara cada lado, 0 que nos da os pontos 0 e 5, de onde sa centra, respectivamente, para a construQao do arco. A. designaQao de laneeta dada a este arco e de vida :orma esguia que ostenta.
Areo Ogival Sobrebaixado de 2 Centros (fig. 6).- E..s-e area tambem conhecido simplesmente par ogiva '_ 2 centros e relativamente atarracado, pais que e
mais baixo do que largo. Estabelecida a sua largura a-b, dividimo-la em tres partes iguais e temos as cen- tros 1 e 2. De 1 centramos para b e obtemos 0 area ate e ins- crito na linha do eixo ; e de 2 traQamos para 0 mesmo ponto e fechamos 0 arco. Este arco, quando e ultrapassado, entra na compo- siQao da arquitectura arabe.
Areo Ogival de 3 Pontos (Fig. 7). - Este arco constroe-se num triangulo equilatero, pois que a sua al· tura e igual a sua largura. Estabelecida a largura do arco a-b, centra-se em a e tiramos urn arco de b ate a linha do eixo no ponto e e reciprocamente centrando em b tiramos de a urn arco para e, fazendo-se a ligaQao do conjunto;
Areo Ogival Sobl'ebaixado de 4 Centros (Fig. 16).
Areo Tudor (Fig. 17). - Este arco e uma das mais belas caracteristicas da arquitectura ingle~a, do estilo tudoresco, de on de the vem 0 seu nome. E conhecido tambem pOI' ogiva inglesa. 0 seu traQado e urn tanto curioso, como vamos observar. Achada a largura do vao na linha a-b, marca-se a liDha do eixo, dividindo-se essa largura em quatro par- tes iguais, a, e', e, ell, b ; depois tira-se urn arco de a com 0 raio a·e" ate a linha do eixo, dando os pontos e e e na linha do eixo e 0 mesmo se fazendo centrando em b, ficando determinada a altura do arco em e. De e' e e" traQam-se linhas para e, que servirao de limite as partes da construQao do arco. Em seguida centra-se de e' com raio em a urn arco ate a recta e'-e, fazendo-se 0 mesmo centrando-se de e" ; depois, finalmente, termina-se a construQao do arco com rectas ligan do os arcos ate a sua altura, e, desde as li- gaQoes das linhas e-e e e"·e.
Areo Aviajado dado 0 Vao (Fig. 4). - Dada a 1ar-
de-se esta em tres partes iguais, sendo uma delas 1-B. De 1 tira-se a distancia t-B e marca-se na linha ver- tical e-e' a ponto 2. Seguidamente de 1 centra-se de B para e, e de 2 centra-se de e para a, passando sobre a linha A-B.
I .,^ I , I ""-,,,'" '*~: ....•. ....""/ I ... )/~ C' 4 ('II '" 1J
",.,/. ... -' 'I
. ,
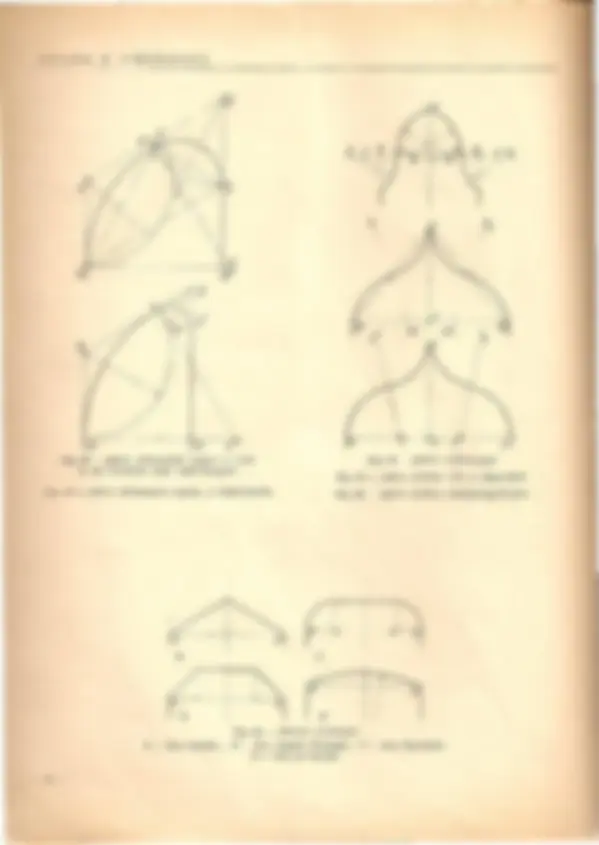
Fig. 14 - ARGO OGIVAL DE 4 GENTROS Fig. 15-ARGO DE FNRRADURA
B e a san as ombreiras do VaG em que se apoia 0 arco. As caracteristicas deste tipo de arcos san estarem as suas nascen<;{as em pIanos diferentes.
Areo Aviajado dado 0 Vao e a Linha das Naseenr;as "Pig. 18). - Estabeleclda a linha das nascen<;{as a-b com a largura do van a-b", tiram-se destes pontos ver- 'cais elevadas para os pontos a'-b', a que se ligam por nma recta paralela a linha a-b. Depois, centrando-se de a' para a traQa-se urn arco de circulo que nos vai dar 0 ponto e na linha ai-b. De b' centra·se para b e tira-se nm arco para a recta a'-b', onde marcamos 0 ponto d. ~eguidamente desenhamos as eordas destes dois arcos que se interceptam num ponte e, e de on de tiramos uma ecta perpendicular a linha a'·b', que vai encontrar a' horizontal a-b", marcando 0 ponto f.
ara nos dar 0 ponto g. Terminada a constru<;{ao fazemos 0 trac;ado: de f ti-
1. mos 0 arco de nascenya a ate e,. e do ponto 0 g conti~ ~uamos 0 arco de e para a nascenc;a b, terminando 0 e::rndo.
A7'COAviajado dada a Tangente (Fig. 19). - Esta-
Seguidamonte tira-se de a com qualquer raio; urn arco de clrculo em cujo exemplo marcamos al^ e ,ai dar na tangente 0 ponto e; de b com 0 raio de c tiramos urn arco para a linha vertical bob', on de marcamos 0 ponto h'l. Do ponto confll).ente e tra<;{amos uma recta perpen- dicular a linha a-b e que atingindo a horizontal a'-b' prolongada. nos da 0 ponto d. Do ponto b'l^ tiramos uma horizontal que toca a linha cod, inscrevendo 0 ponto e. Finalizada a construc;iio vamos fechar 0 arco: de d trac;amos 0 arco de a' para e e centrando em e conti- nuamos 0 area de .~ para b", terminando 0 problema convenientemente.
Areo Aeeolado (Fig. 20). - TraQada uma linha ho- rizontal inscreve-se nela a largura do 'laO, A-B, que se divide em seis partes iguais, que marcamos pelos pon- tos A, a, ai, e', b', b, Be dao se .duas dessas partes para cada lado do arco, no prolongamento da linha A-B, que san os pontos 1 e 2. Do ponto e', que e 0 centro da recta A-B, tira-se a respectiva linha do eixo, sempre necessaria a constru- Qiio dos arcos..
__ 1 __ ",.,,-" ··e ....', / "^ / I ,, /' /' I " I -i-.. I , / I', I I \ I ' I. \ I \1/ \ I
h'ig. 16 - ARGO OGIVAL SOBREBAJXADO, DE 4 GENTROS
Fig. 24 - DIVERSOS SIMPLES PARA A CONSTRUQAO DE ARCOS (A e B)
~ Seguimos a eonstrUC;3.o: de a' tira-se urn area de b para e e de b' sai tambem urn area de a para e,fieando assim construida urna ogi va. Depois, de 2 tiram-se raios que de a ou de b, respeetivamente de urn e outro lado do area ogival, ligam com as ombreiras do vao, linhas que eaiem de A ou de B. Este area tamMm tern a designac;3.o de area ogival ultrapassado.
Arco Duplo de 4 Centros (Fig. 21). - Estabeleeida a linba horizontal a.b, que e a largura do V3.0do areo, trac;a-se a sua linha de eixo e temos os 1>ontos c e d. De e tiramos uma linha obliqua para a e outra para b, que dividimos ao meio. De seguida aehamos os eentros triangulares das me- tades das linhas obliquas, a que darnos os numeros 1, 2, 3 e 4, de onde tiramos os respeetivos areos que se eombinam a meio das obliquas.
Areo Duplo Sobrebai;rado (Fig. 22). - Divide-se a linha horizontal a-b em tres partes iguais, sern termos deixado de inserever a linha do eixo e'·e e estabeleee- mos os pontos 1 e 2. A altura do area e Dotada no ponto e. Centrando-se em 1 com a distaneia a-2, mareamos um area e eentrando em e com urna distaneia igual a a-1 fazemos( a interseec;ao desse mesmo areo, dando 0 ponto 3. Para a obtenc;ao do ponto 4 proeedemos de igual maneira, mas no sentido inverso.
Centrando de 1 para a traQamos um area ate a Hnha 1·3, e eentrando em .q ligamos com urn novo area 0 an~ terior, que atinge 0 ponto c. Do lado b·c proeedemos igualmente e feehamos a eonstruQao.
Fig. 25 - DIVERS OS SIMPLES PARA A CONSTRUQAO DE ARCOS (0 e D)
Areo Angular (Fig. 23-A). - A eonstruQ3.o deste area eonsta apenas, depois de estabeleeida a largura do vao e aehada a respeetiva altura - 0 vertice, da liga<;3.o dos tres pontos entre si. A largura do vao a-b e dividida ao maio e e nessa linha do eixo, como se eompreende, que se ligam as obliquas said as respeetivamente de a ou de b. Este areo tamMm e eonheeido por area quebrada.
Area Angular Truncado (Fig. 23-B). - Estabeleeida a largura do vii-o na linha a-b e demareada tambem a sua altura, eortamos os dois angulos a 45°, fieando assim obtida a eonstru~ao regular, Porern, qualquer outra in- elina<;ao e adrnissivel nestes tipos de areos. Areo Deprimido (Fig .. 23. C). - Este areo, que nlio tern nada de extraordiIHl.rio senao apenas 0 arredonda- mento das extremidades da sua verga, sobre as suas ombreiras e, como se ve, de uma grande simplieidade. Os eentros, para se estabeleeer os raios para os arre- dondamentos, sao aehados na pr6pria linha a·b, que e a largura do vao.
Areo Plano. - Este area e eonstituido por uma verga em angulo recto sobre as ombreiras; a linha das naseenQas e normal ao plano das testas. Tambem e designado area recto e area direito. A de- nominaQ3.o de areo a esta eonstruc;ao e talvez poueo eerta, porque 0 nome de areo da-nos sempre a ideia de uma cui-va. As' pedras ou tijolos da eonstruQ3.o eonvergem para urn ponto situado na linha do seu eixo.
CONSTRU<;AO
pA.RA se efectufl:r a constru<;;ao dequalquer tipo de arco, e mister construir previamente a respectiva cambota ou simples. Os simples que sao arma<;oes de madeira com a forma do arco que se pretende construir no seu exterior, sevem para ,apoio da constru<;ao. Os comptimentos dos simples sao .iguaisas espessuras das obras que tern de acompanhar. Assim se 0 arco mede de espessura 0, tern a cambota de tel' de cbmprimento essa mesma di- mensao. As cambotas, que tamhem sao conhecidas pela desi- gnaQao de cimbres, t~mexteriori:riente a forma do arco a construir... A sua construr;ao faz-se dispondo no chao as tllbuas apropriadas a esse stlrvir;o, que se sobrepregam umas nas outras, e achando 0 centro do arco com a sua pr6- pria dirilensao em tamanho natural, trar;a-se' 0 arco com um cintel oucom uma fasquia ouum cordel a servirem de comrasso, no que se refere a areos de volta perfeila. Se se tratar dB urn arco abatido ou ogival desenha-se no chao todo 0 trar;ado no tamauho natural, ficando, porem, sobre as tabuas ali dispostas 0 tr~1(;ado do arco, para depois se fazer 0 corte arredondado com a serra de rodear. Estes pedar;os de tabuas arredondadas, que sao as t;erCeas, e que se pregam umas nas ootras e que, como ja dissemos, tem exteriormente a forma do arco, sao fixadas no seu diametro pOl' um frechalou travessanho, que rE:jcebe as escoras para 0 seu bom travamento. As ligar;oes das cereeas entre si podem ser fsitas de diferentes maneiras, como vemos pos desenhos.
Fig. 26 - CAMBOTA PARA A CONSTRUQ.AO DOS ARCOS OGIV AIS
DOS ARCOS
As Figuras 24 A e B e 250 e, D apresentam os sim- ples colocados na construr;ao de arcos de volta p.erfeita. o numero de pe<;;asa prefazer a volta completa do arco e varia vel, consoante a 'grandeza da obra a construir. Se se utilizar tabuas largas necessitamos de menos peQas, mas se empregarmos madeira estreita, precisamos maior numero de cerceas. A espessura destas titbuas nas peguenas cambotas, deve ser de cerca de 0,03 ou 1 fio de madeira de pinho da terra. A fixa<;ao de uma as outras deve ser feita com pregos de setia. Nas grandes cambotas e conveniente a aplicaQao de madeiras grossas. o corte das cerceas deve ficar perfeito, quando os simples se destinarem a arcos de tijolo. Para as obras de cautaria de p'e<:asrelativamente grandes e sem sime- tria, ja a boa perfei<;;ao nem sempre e exigida, como se compreende. A arma<;ao dos simples e em geral constituida de duas grades, como apresentamos nos desenhus, ligadas entre si com ripas ou reguas na formaQao do arco da cambota, no c.omprimento correspondente a espessura da obra. Essas reguas tern geralmente a desigua<;;iio de eoxins. Quando 0 arco e de grande espessura, a cambota pode comportar diferente DamBra de grades, pois que o espaQo conveniente entre estas e apenas de 0, .. As .cambotas sao assentes sobre motivos salientes dos pes direitos (Figs. 24 B e 2b D), ou na falta deles sobre prumos de madeira fixados ou apoiados no chao (Figs. 24 A, 25 B, 21), 27 e 28). A fixa<;;aodas cambo- tas ou simples tern de ser perfeita, bem nivelada e apru- mada; desses principios depende a boa seguran<;;a da obra e 0 bom aspecto do arco. ' Os simples devem ficar bem resistentes, pQis que a construQao que terao de suportar e sempre, qualquer que seja 0 material empregado, muito pesada. Quando os arcos sao muito estreitoR, as veztlS cons- troem-se os simples com madeira grossa, evitando-se as- sim a constru<;;ao de mais de uma grade, tornando-se tambem pOl' isso muito econ6mica, po is se prescinde do emprego de ripas ou reguas na formar;30 do arco. Na Figura 32 mostramos uma combota de relativo
. comprimento. As combotas (1) de maior dimensao, sao aquelas que se destinam as ab6badas de berr)o e de asa de cesto. No entanto, tambem pOl' vezes' se constroem arcos de dezenas de metros, como esses que sustentam ruas sobre eles. ' ' As dimensoes dos arcos SaD variaVeis, dependendo sempre e s6 do projectoda obra.
(1) Em gel'al quando as cambotas sao de gl'andes dimensoes, 's se deslgnam POl" simples ou cimbres.· ,.
A B 6 B
t\ s ab6badas SaG construQoes de ordem curvilinea, de ..I. cantaria, de alvenaria de pedra e de tijolo, e tern :fO destino a cobertura de edificioB ou as suas depen- 'encias e outras obras de fins especiais, como reserva- :6rios tuneis, etc. As suas formas podem ser as mais variadas, depen- endo apenas do local onde se construam e da obedien- cia ao projecto da obra, que lhes dara 0 aspecto mais con,eniente. As ab6badas podem ser reetas ou planas, dlindrieas, de berr;o, de arestas, de barrete de elerigo, de lunecas e de cupula, quanta a forma dos seus arcos, e direitas, en- -ciesadas. curvas -ou in elinadas, quanto a sua directriz. Estas construQ5es podem cobrir espaQos quadrados, rectangulares, paralelogramicos e quaisquer outros em que os seus nascimentos possam assentar. Os traQados das ab6badas obedecem aos mesmos principios dos traQados dos arcos. Algumas ab6badas SaG de grande efeito construtivo a, sob 0 ponto de vista ornamental, apresentam por ve- zes uma imponencia, apreciavel Quando SaGconstruidas em cantaria, 0 aparelho das pedras obedece as conver- gencias da estereotomia. As ab6badas construidas de ti- •010 rebatido SaGrebocadas nointradorso, que serve de -ecto para as dependencias que cobre. Nas obras de alvenaria de pedra com argamassa de cimento e areia, tambem se aplica 0 reboco, pois este trabalho deve fiear acabado como ficam todas as outras al,enarias, e 0 intradorso de uma ab6bada e, acentuamos, um tecto como qualquer outro. As ab6badas de cant aria SaG sempre aparelhadas no intradorso e, algumas vezes, tambem 0 saG no pr6prio extradorso. De uma maneira geral, a maioria das ab6badas nao fica com 0 extradorso a vista, antes costuma ficar nive- lado com alvenaria ou betao, afim de receber urn pavi- ento ou qualquer outra obra que lhas fi4ue superior. A eonstruQao das ab6badas eom tijolo e alvenaria de pedra, e em tudo analoga a construQao dos arcos dos masmos materiais. A constru"<;ao de cantaria difere urn ouco: enquanto nos arcos, se saG estr,eitos, uma s6 pe· dra compoe toda Do espessura, se nao largos, em geral,
A D A s
todo 0 intradorso e decorado, composto por conseguinte com varia!! pedras na largura, concordantes com a espes- sura; nada disso, porem, sucede nas ab6badas. As pedras SaG dispostas e assentes com as suas jun- tas ou espessos desencontrados, e ligaudo-se homogenea- mente com as pedras dos pes direitos. A classificaQao das ab6badas e curiosa e vem, como se sabe, dos mais remotos tempos. Vamos explica·la:
Ab6bada de bergo (fig. 17)- J!jsta ab6bada, tambem designada eilindriea, e de todas 110 mais simples, pois e constituida por arcos de volta perfeita (i). A sua cons- tru<;ao pode ser enviesada e montante, como acontece com os areas.
Ab6bada abatida- A ab6bada abatida ou de asa de cesto s6 difere da de berf]0, por ser constituida por arcos abatidos ou de asa de cesto. Tambem se constr6i com areos de gear9ao.
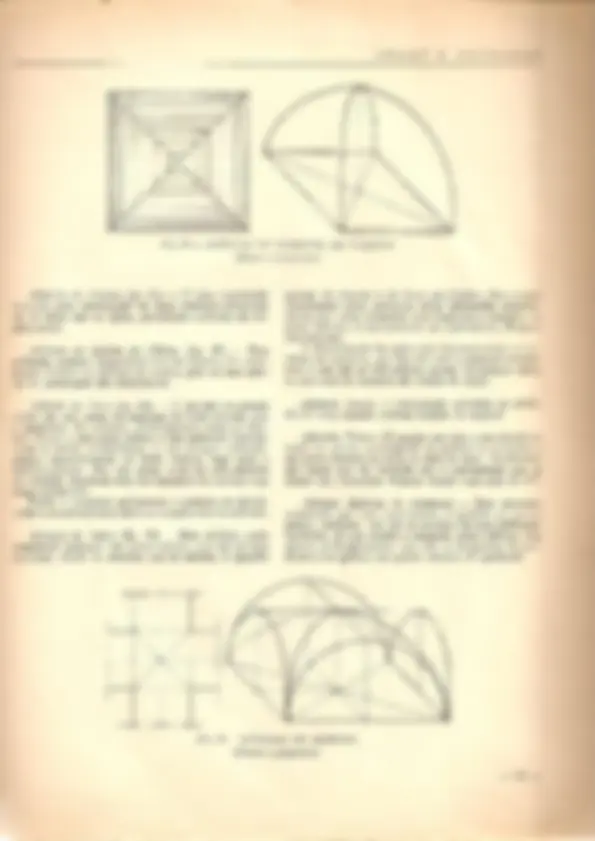
Ab6bada Esferiea ou de (;upula (fig. 29) - Esta curiosa ab6bada nasce apoiada numa constru<;ao conti- nua au circular, denominada tambor e nao necessita de simples. Vai-se eregindo por fiadas ate se fechar com- pletamente. Basta apenas urn born andaime para os pe- dreiros poderem trabalbar a vontade. Para maior estabilidade da COnstrllQaOe conveniente, quando se apr6ximar 0 seu fim, assentar provisbria- mente no seu lugar, os feehos ou chaves da ab6bada, ate se fechar totalmente a sua coroa. Questao apenas de se equilibrar a terminaQao da obra. Esta cupula, que e uma sucessao de circulos concen- tricos· montados uns sabre os autras, tambem pode ser construida com arcos parciais formando uma ossatura arqueada para suporte de toda a obra. Tambem e conhecida por ab6bada de revolw)i'io.
(I) A abObaba de ber90 tambem erradamente e chamada ab6- bada de canudo, nome fora de prop6sito.
(Planta e corte)
Fiy. 30 - ABOBADA DE BARRETE DE CLERIGO (Planta e perspectiva)
Ab6bada de Arestas (fig. 31). - "It uma construQao formada pela intersecQao de duas ab6badas eilindrieas ou de berfio que se ligam, geralmente cortadas em an- gulo recto.
Ab6bada de Barrete de Clerigo (fig. 30). - Esta ab6bada, tambem chamada de area de elaustro, e a cons- truQao inversa da ab6bada de arestas, pois as suas ares- tas de penetraQao san reentrantes.
Ab6bada de Cave (fig. 33). - "It urn tipo de arcada muito em uso antes do emprego do betcio armado, que a suplantou. No entanto, ainda algumas vezes se cons- tr6i. Como 0 seu nome indica, a sua aplicaQao destina- va-se a cobrir subterraneos e era sempre sobrecar- regada superiormente de betao magro, logo' ap6s 0 descintramento. Sao, em geral, areos de volta perfeita ou abatidos. Resistem bem aos impulsos do terreno com larga resistencia. Sobre 0 massame aplicava-se 0 sobrado do res-do- -chao e os subterraneos ficavam completamente estaveis.
Ab6bada de Ogiva (fig. [;8). - Esta ab6bada pode comportar qualquer dos arcos ogivais, que san as suas nervuras, des de os abatidos aos de lanceta. "It questao
apenas de simples e de bons pes direitos. Nas antigas construQl'les estas ab6badas eram reforQadas exterior- mente por areos aviajados, que tomavam a designao de areos botantes e descansavam em contrafortes designa- dos botareus. A denominaQao de ogiva vem dos seus arcos ou ner- vuras em cantaria, que Ihe dao toda a ossatura constru- tiva e que san as verdadeiras ogivas. Os espa<;os entre as nervuras de cantaria san cheios de tijolo.
,Ab6bada Anular - besignaQao atribuida as ab6ba- das de berfio quando cobrem escadas de caracol.
Ab6bada Plana-"It aquela que tern 0 seu intradorso recto ou plano, convergindo as pedras ou os tijolos a urn ponto situado na linba do eixo do arco. Na constru- Qao deste tipo de ab6bada nao e conveniente que as juntas das impostam formem angulo com mais de 60°,
Ab6bada Esferiea de Pendentes - Esta ab6bada, constituida por uma semi-esfera, e apoiada em quatro planas verticais, que san as paredes de uma edifica<;ao quadrada, de que resulta a chamada ealote esferiea, com quatro prolongamentos, que tern a designaQao de pen- dentes e se apoiam nos quatro vertices do quadrado.
,,
~ I - .••.•. .'I -_- .... ~,'",. :
.• e"" ••. _ ,,' "I -~ _ •••• " •••-I
Fig. 31 - ABOBADA DE ARESTAS (Planta e perspectiva)
I
1
I
.
I I o ____ .~ J
A construQao das ab6badas na actualidade s6 e jus- tificavel na continuaQao de edificios antigos, em que e mester manter a sua traQa primitiva, mas, nesses casos, nao tern Ia Iugar 0 betao armado. No entanto, isso e com os construtores.
superior e na espessura e resist(}ncia dos pes direi- tos, que the dao 0 mais forte apoio. A impulsao das ab6badas e 0 esforQo que exerce sobre os seus pes dil'eitos, na0 tern 0 mesmo valor nos di versos tipos e sistemas destas construQoes. As ab6badas cilindricas e as de coroa elevada, como sejam as ogi~ais, apresentam maior estabilidade e po- dem suportar grandes cargas sabre 0 fecho. A impulsao nestas ab6badas a quase vertical. Desde a nascenQa da ab6bada ate a sua coroa, toda a resistencia da obra reside nos rins, parcela, de arco situado entre esses dois pontos ,culminalltes. As vezes os extradorsos' sobre os rins sao reforQados 'na sua es- pessura. Em resistencia seguem-se as construQoes de arcos abatidos e elipticos. Nas ab6badas destes tipos a impul- SaG aumellta a medida que a ftecha do arco diminui. A construQao dos pe,; direitos, dos arcos e ab6badas obedeee as leis da estatica, como a de contar, mas 0 es- tudo dos calculos de estabilidade e, a bem dizer, muito recente, enquanto que a cOIlstruQao das ab6badas vem de recuados seculos. A forma de obter a espessura dos pas direitos usada pelos construtores do seculo XVI, e que tao bons resul- tados dava, a ponto que ainda hoje as ab6badas cons- truidas entao, garantem a mais s61ida das resistencias, e muito pratiea. Consiste esse traQado (fig. 36) no seguinte:
Estabelecida a linha das nascenQas de qualquer arco, de volta perfeita, abatido ogival, ou ainda outros, divide- -se 0 pro.prio ~rco em tres partes iguais e damos-Ihe os pontos c e d, alem de a-b da linha recta horizontal, pon- tos estes que correspondem as nascenQas ; seguidamente
tiramos uma recta de d para b, que se prolonga par baixo ate encontrar um arco de circulo centrado em JJ e com 0 raio em d. A intersecQao deste arco com a ob " qua d-b da-nos a verdadeira espessura do pe direito.
NAS ab6hadas de cantaria 0 aparelho das aduelas deve ser muito cuidado e 0 trabalho da construQao, que a 0 seu assentamento, exige uma certa paricia do eons- trutor e dQS seus operarios. Jil mesmo 0 simples deve ser melhor construido e na pr6pria grade da eambota, devem estar marcados todo! os espessos das pedras da respeetiva convergeneia, para que, no assentamento, cada uma das aduelas fique no seu lugar pr6prio, conseguindo-se assim a perfeiQ3.o do arco. As juntas entre as aduelas oscilam de 0,008 a 0,012: para que nao seja muito delgada a camada de argamassa. Quando as aduelas saode grandes dimensoes, as juntas, entre si, podem chegar a 15 milimetros. As juntas devem ficar com igual folga desde 0 in- tradorso ao extradorso, e a camada de argamassa de,e ser da mesma espessura em toda a extensao.
1."'- 1/ -...,~,.._ ... a , h i.. I ",
Fig. 36 - TRAQADO PARA OS PES DIREITO DAS AB6BADAS
I -+--I
Uma ab6bada bem construida deve manter entre to- das as aduelas as juntas de igual espessnra. Por meio de eerceas bem eortadas marea-se 0 espes- so de eada aduela, e pela mareac;ao do simples regula-se optimamente 0 assentamento de todas as fiadas. Depois de feito 0 assentamento das Impostas eomec;a- -se 0 assentamento das aduelas, por fiadas de um e outro lado do area simultaneamente, para que 0 simples fique carregado por igual, ate se ehegar ao fecho da ab6bada. as espessos das pedras devem ficar desencontrarlos, como e de saber, para 0 bom travamento da obra. o simples, estando sempre uniformemente carregado. da melhor garantia it construc;ao, pois e sabido que a pressao sobre a argamassa das juntas das aduelas e igual em todas elas. Termina-se a constru(,(ao da ab6bada com 0 assenta- mento do fecho, que deve ficar apertado e batido a masso. Descintra-se ap6s a conclusao do trabal ho, dando- -se imediatamente 0 assentamento da ab6bada, cujo fe- cho e de novo batido. Para a constru(,(ao destas ab6badas SaD igualmente pr6prias as argamassas de cimento e areia, ao tra(,(o de 1 : 4 e 1 : 5 ou como melhor convier.
I I I I i i
DESCINTRAMENTO
DAS ABOBADAS
o descintramento das ab6badas e, como atras disse- mos, feito logo ap6s a conclusao dos trabalhos nas obras de cantaria, e s6 passado algum tempo, mas ainda com as alvenarias frescas, nas obras de tijoJo. Como nestes trabalhos, e em geral em todas as alve- Darias, se da 0 assentamento, logo DaO convem que ja estejam secos Da altura do descintrameDto, pois que a obra poderia desligar-se pareialmente, casu que se DaO da estando ainda as massas relativameute frescas. o descintramento deve fazer-se cuidadosamente, ali- viando-se os simples com as suas escoras a pouco e pou- co, para que as liga(,(oes nao se quebrem, 0 que aconte- ceria se 0 trabalho fosse feito bruscamente. 0 trabalho de deseintar uma ab6bada deve durar, pelo menos, meia duzia de dias, pois que 0 descintramento das eam- botas deve ser muito lento. Em obras de grande categoria os simples sao trava- dos, por meio de parafusos assentes nos prumos de apoio, que depois, vagarosamente, se desapertam, dei- xando-os descer. subtilmente, nivelada e paralelamente.
. II L. _
, I J I I I.