Download TURBOMACCHINE intro da almeno una palettatura rotante (girante) disposta su di un disco and more Study notes Engineering in PDF only on Docsity!
Laurea a Distanza in Ingegneria Meccanica – Corso di Macchine
5. TURBOMACCHINE
5.1 INTRODUZIONE
5.1.1 LA TURBOMACCHINA ELEMENTARE
Una turbomacchina è costituita da almeno una palettatura rotante ( girante ) disposta su di un disco, interessata dal flusso di un fluido (compressibile o incompressibile). Le forze che si generano tra fluido e palettatura danno luogo allo scambio di lavoro tra la macchina ed il fluido.
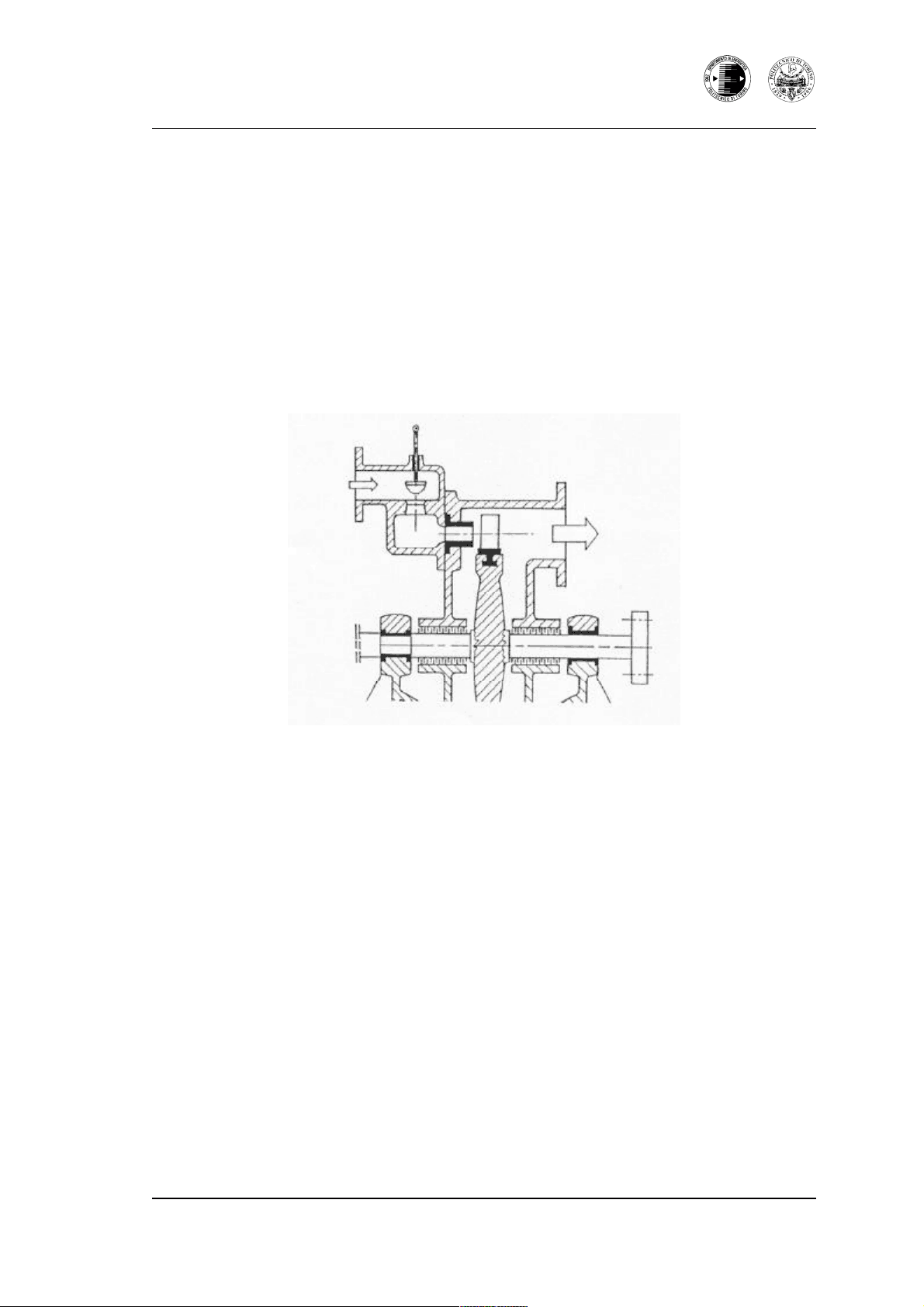
Figura 5.1 : Schema di turbomacchina motrice.
E' poi in genere presente anche una palettatura fissa (che nelle macchine motrici precede la palettatura mobile, mentre in quelle operatrici la segue), con la funzione di trasformare l'”energia di pressione” in energia cinetica (e prende allora il nome di effusore) o viceversa (e si chiama allora diffusore), evidentemente senza scambio di lavoro con il fluido. L'insieme della palettatura mobile e di quella fissa costituisce uno stadio della turbomacchina. Nell'ambito della presente trattazione si effettuerà un'analisi fluidodinamica di funzionamento della turbomacchina di tipo "unidimensionale": secondo questa ipotesi, si suppone che tutte le proprietà (cinematiche e termodinamiche) che caratterizzano lo stato del fluido siano costanti in ciascuna sezione dei condotti fissi e mobili della turbomacchina. Questa approssimazione comporta l’utilizzo di opportuni valori medi delle proprietà di ciascuna sezione; eventuali errori o imprecisioni nella valutazione del comportamento fluidodinamico reale vengono tenuti in conto per mezzo di opportuni coefficienti correttivi. L’ipotesi di flusso unidimensionale presuppone:
Laurea a Distanza in Ingegneria Meccanica – Corso di Macchine
- altezza delle palette l sufficientemente piccola rispetto al diametro d della macchina (il che comporta che la velocità periferica sia pressochè la medesima alla radice e all’estremità della pala), ovvero :
<< 1 d
l ;
- spessore delle pale trascurabile;
- numero di palette sufficientemente alto, per poter considerare la larghezza del canale fra le pale costante sia alla radice sia alla base.
5.1.2 NOMENCLATURA
La nomenclatura è analoga a quella adottata per i profili alari, essendo le palettature a tutti gli effetti superfici aerodinamiche:
Figura 5.2: Palettatura a schiera in una turbomacchina (profili delle palette in sezione).
- c1 e c2 : velocità del fluido in ingresso ed uscita dalla palettatura;
- α 1 ’ e α 2 ’: angoli di attacco e di fuga del profilo;
- angolo θ = α 1 ’ - α 2 ’: inarcamento del profilo;
- α 1 e α 2 : angoli cinematici di ingresso e di uscita dal profilo;
- i = α 1 - α 1 ’: angolo di incidenza sul profilo;
- δα 2 = α 2 - α 2 ’: angolo di deviazione ;
- ε = α 1 - α 2 : angolo di deflessione della vena fluida nel palettaggio;
- t e b : passo e corda della schiera di palette;
- σ = b / t : solidità della schiera di palette.
Ventre (intradosso)
Dorso (estradosso)
Laurea a Distanza in Ingegneria Meccanica – Corso di Macchine
monte della girante, la parete ideale 2-2 all’uscita della girante, e le pareti (ideali o reali) di confine della palettatura ai raggi esterno ed interno (figura 5.4).
Figura 5.4: Definizione del volume di controllo nel vano di una palettatura mobile di una turbomacchina per il calcolo del lavoro interno.
Dopo un intervallo infinitesimo di tempo dt la massa di fluido sopra definita si sarà spostata nel verso del flusso, andando ad occupare lo spazio compreso fra le superfici 1'-1' e 2'-2', rispettivamente all’ingresso della palettatura e distante a valle di una quantità dx. Nell’ipotesi che il moto sia stazionario, è possibile scrivere:
M = dM 1 + Mg = Mg + dM 2 ,
dove con Mg si è indicata la massa contenuta all’interno del vano della girante. Dalla precedente relazione risulta che la massa dM 1 contenuta nel volume infinitesimo racchiuso dalle superfici 1-1 e 1’-1’ è uguale alla massa dM 2 contenuta nel volume infinitesimo delimitato dalle superfici 2-2 e 2’-2’. La variazione del momento della quantità di moto – rispetto all’asse di rotazione della macchina – della massa M nell’intervallo di tempo dt considerato può essere scritta come segue:
dK = dM 2 ⋅ cu 2 ⋅ r 2 − dM 1 ⋅ cu 1 ⋅ r 1 = dM ⋅( cu 2 ⋅ r 2 − cu 1 ⋅ r 1 ),
dove r 1 ed r 2 sono i raggi medi della palettatura mobile rispettivamente all’ingresso ed all’uscita. In base al teorema del momento della quantità di moto (si veda il Capitolo 3), trascurando le componenti tangenziali delle forze di attrito del fluido sulle pareti fisse, la coppia C scambiata tra palettatura e fluido vale
m ( c 2 r 2 c 1 r 1 ) dt
dK C = = &^ ⋅ u ⋅ − u ⋅ ,
asse di rotazione
w della macchina
r 1
r 2
Laurea a Distanza in Ingegneria Meccanica – Corso di Macchine
nella quale m &^ rappresenta la portata in massa di fluido attraverso la palettatura. La coppia C è il momento che la palettatura applica al fluido; cambiato di segno è il momento che il fluido applica alla palettatura. Moltiplicando C per la velocità angolare ω della girante, si ha la potenza interna scambiata. Poichè u = r ω , si ottiene:
Pi = C ⋅ω = m & ( cu 2 u 2 − cu 1 u 1 ).
Tenendo poi presente che la potenza può essere espressa come prodotto della portata di massa per il lavoro dell'unità di massa, si ha che il lavoro interno vale
c 2 u 2 c 1 u 1 m
P
L (^) i = i = u − u &
La precedente espressione rappresenta il lavoro compiuto dalla palettatura su ogni chilogrammo di fluido che la attraversa (o lavoro massico della turbomacchina). Il valore numerico che ne risulta è positivo quando è applicata ai triangoli delle velocità tipici di una macchina operatrice (compressori, pompe); se viene applicata ai triangoli di velocità tipici di una macchina motrice (turbina), essa restituisce un valore negativo, come è logico attendersi (in quest’ultimo caso è il fluido a cedere lavoro alla palettatura). Per evitare di dover ragionare in termini di potenza negativa, nel caso delle turbomacchine motrici si fa comunemente riferimento al concetto di lavoro ottenuto ; ciò è equivalente a cambiare il segno a secondo membro nelle espressioni precedenti quando sono impiegate per le macchine motrici:
Macchine operatrici Li = u 2 ⋅ cu 2 − u 1 ⋅ cu 1 ,
Macchine motrici L (^) ott = - Li = u 1 ⋅ cu 1 − u 2 ⋅ cu 2.
E' importante rilevare che l’espressione del lavoro interno dipende solo dal valore delle velocità, ed è valida sia in assenza sia in presenza di forze di attrito interne al fluido o al contatto fluido-parete (con l'unica eccezione delle componenti tangenziali sulla superficie di contenimento fissa, in genere trascurabili); essa è dunque utilizzabile sia nello studio del funzionamento ideale sia di quello reale della macchina. L'espressione del lavoro scambiato tra la macchina ed il fluido che la attraversa può essere scritta in una forma diversa da quella appena ricavata. Per il teorema di Carnot, infatti, valgono le espressioni seguenti:
2 2 2
2 2
2 2
2 2
1 1 1
2 1
2 1
2 1 2 cos
2 cos α
α w c u c u
w c u cu = + −
e quindi
2 2 2 2 2 (^222222 )
2 1
2 1
2 1 1 11 1 1 cos 12
cos 12 uc uc c u w
uc uc c u w
u
u = = + −
α
α ,
da cui
L i = cu 2 u 2 − cu 1 u 1 = 1 2 ( c 22 − c 12 + w 12 − w^22 + u 22 − u 12 ).
E' utile osservare che alla stessa espressione si perviene applicando il Primo Principio della Termodinamica (in forma Euleriana per i sistemi aperti) alla
Laurea a Distanza in Ingegneria Meccanica – Corso di Macchine
5.1.5 LO STUDIO DELLE TURBOMACCHINE IN SIMILITUDINE
Il concetto di similitudine è molto importante nello studio delle turbomacchine, perchè consente di estendere a tutte le macchine simili le considerazioni ed i risultati delle analisi svolte su una singola macchina. L’espressione del lavoro scambiato tra fluido e palettatura mobile può essere riscritta mettendo in evidenza una delle velocità, ad esempio u 1 :
1
1 1
2 1
2 2 1
2 2 1
1 1
2 1
2 2 (^2 2111) u
c u
c u
u n d u
c u
c u
u L (^) i cu u cuu u u u π u u.
Il termine tra parentesi contiene solo rapporti di velocità, che, in stadi geometricamente simili e funzionanti con triangoli delle velocità simili , assumono lo stesso valore. La costanza del termine tra parentesi, e cioè la similitudine di funzionamento , comporta dunque la similitudine geometrica delle macchine (evidente nella costanza del rapporto u 2 /u 1 , uguale naturalmente al rapporto r 2 / r 1 ), ma anche la similitudine fluidodinamica, poichè anche le velocità del fluido devono variare in proporzione (ed essere ugualmente orientate); ad esempio, due diverse condizioni di funzionamento di una stessa macchina possono essere o no in similitudine pur essendo la macchina geometricamente simile (anzi uguale) a se stessa. Qualora sia verificata la similitudine tra due macchine a e b , varranno dunque le relazioni
2 2
2 2
cos
cos
ib b b
ia a a L t n d
L t n d
= ⋅
e dunque
2 2
2 2
b b
a a ib
ia n d
n d L
L
Le equazioni precedenti mostrano dunque che i lavori interni delle due macchine stanno in rapporto come i quadrati del prodotto tra la velocità di rotazione delle macchine e il diametro medio (le dimensioni delle macchine). Si vedrà più avanti come le perdite principali caratteristiche delle turbomacchine siano anch'esse proporzionali, in prima approssimazione, ad un quadrato di velocità; ne segue che il rapporto fra il lavoro scambiato e le perdite, in condizioni di similitudine (in cui esiste proporzionalità fra tutte le velocità) risulta indipendente dalle velocità stesse, cioè uguale per due macchine operanti in condizioni di similitudine. Poichè il rendimento di una macchina è in qualche modo legato al rapporto fra il lavoro e le perdite, un risultato importante è il seguente:
in condizioni di similitudine, due turbomacchine anche diverse hanno in prima approssimazione ugual rendimento.
La precisazione " in prima approssimazione " è legata ai seguenti aspetti:
Laurea a Distanza in Ingegneria Meccanica – Corso di Macchine
- non è del tutto vero (lo è solo per variazioni contenute delle condizioni di funzionamento) che le perdite sono esattamente proporzionali al quadrato di una velocità;
- la compressibilità del fluido può rendere solo approssimata la similitudine dei triangoli delle velocità sia in ingresso sia in uscita dalla turbomacchina;
- il fenomeno del recupero termico (o del controrecupero) contribuisce alla crescita di importanza dell'aspetto segnalato al punto precedente.
Gli ultimi due aspetti sono legati alla compressibilità del fluido: nel caso delle macchine idrauliche, nelle quali l’effetto di compressibilità è trascurabile, il concetto di similitudine ha di fatto una validità ed una importanza pratica molto maggiore che nelle altre turbomacchine, e viene pertanto utilizzato in maniera molto più estesa.
E' utile estendere le implicazioni legate al concetto di similitudine anche a grandezze quali la portata e la potenza. Volendo qui affrontare l’argomento solo a titolo introduttivo, ci si può riferire, per semplicità, al caso particolare di ad una macchina radiale ( ca = w (^) a = 0 ) centrifuga. Esprimendo la portata con riferimento alle condizioni in corrispondenza della sezione di uscita della girante, di ottiene:
m &^ =ρ 2 A 2 cr 2 =ρ 2 π d 2 l 2 cr 2.
Per analizzare il comportamento di macchine funzionanti in condizioni di similitudine (e quindi simili geometricamente e fluidodinamicamente), la precedente relazione può essere così riscritta:
d n u
c d d
l u u
c d d
l m r^ r 2 2
(^22) 2 2
2 2 2 2
(^22) 2 2
2 & (^) =ρ 2 π =ρ π π.
Poichè i rapporti l 2 /d 2 e cr2/u 2 sono uguali (per due macchine funzionanti in condizioni di similitudine), risulta:
3 m =cos t ⋅ρ 2 nd 2
Nell'ipotesi che sia ρ ≈ cost all’interno delle macchina (ipotesi approssimata per le macchine a fluido compressibile, circa esatta per le macchine idrauliche), si può scrivere:
3 m =cos t ⋅ρ nd 2
Ricordando l'equazione del lavoro interno in condizioni di similitudine, si può esprimere la potenza interna nel modo seguente:
P mL n^3 d^5 i =^ &^ i ∝ρ ,
relazione che mette bene in luce il rapido aumento della potenza di una turbomacchina con le dimensioni (alla quinta potenza) e con il numero di giri (al cubo).
