Datapath and Control in Computer Architecture: A Slide Presentation by Jiang Li - Prof. Ji, Papers of Computer Architecture and Organization

Download Datapath and Control in Computer Architecture: A Slide Presentation by Jiang Li - Prof. Ji and more Papers Computer Architecture and Organization in PDF only on Docsity!

Dept. of Systems & Computer Science, Howard Univ. Jiang Li

The Processor:

Datapath and Control

Dr. Jiang Li

Slides adapted from various sources (e.g. VT, RPI, UCSB etc)

Dept. of Systems & Computer Science, Howard Univ. Jiang Li

Data Path and Control

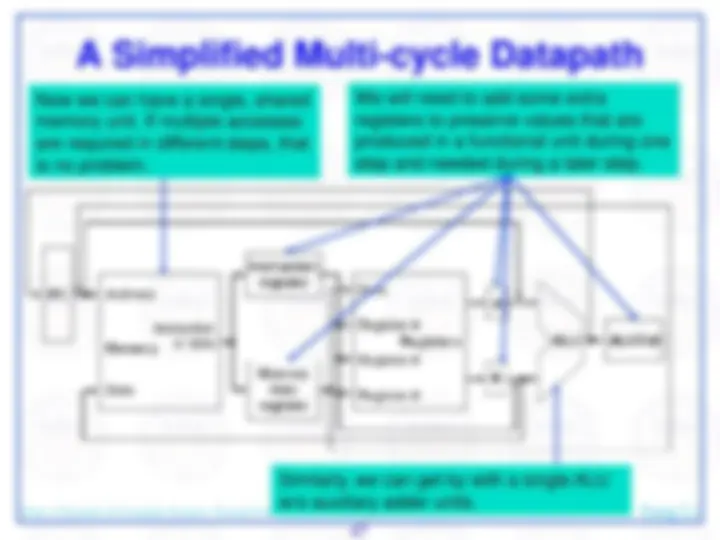
 Data path  The component of the processor that performs arithmetic and logic operations.  Control  The component of the processor that commands the datapath, memory, and I/O devices according to the instructions of the program.

Dept. of Systems & Computer Science, Howard Univ. Jiang Li

Basic MIPS Implementation

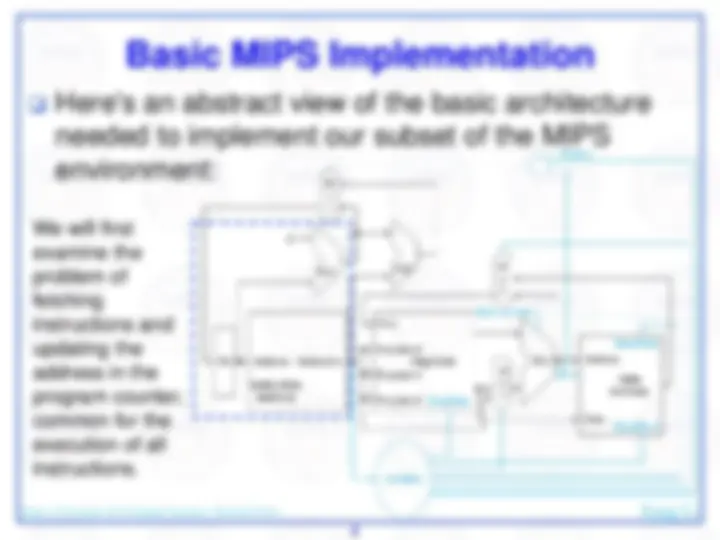
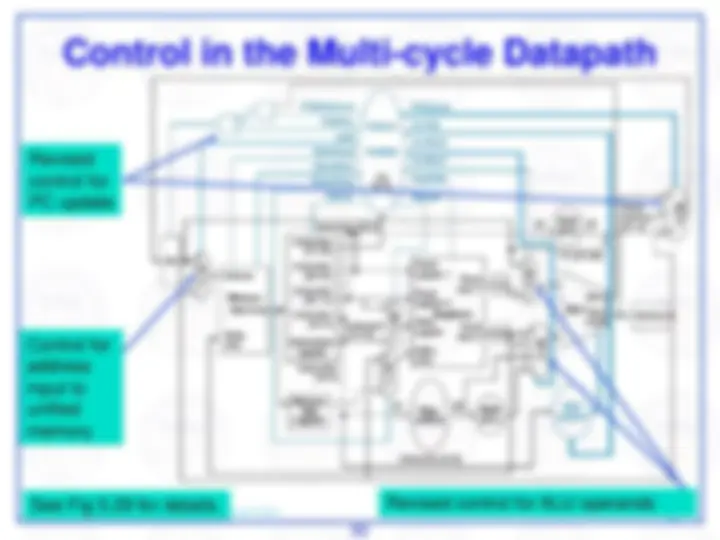
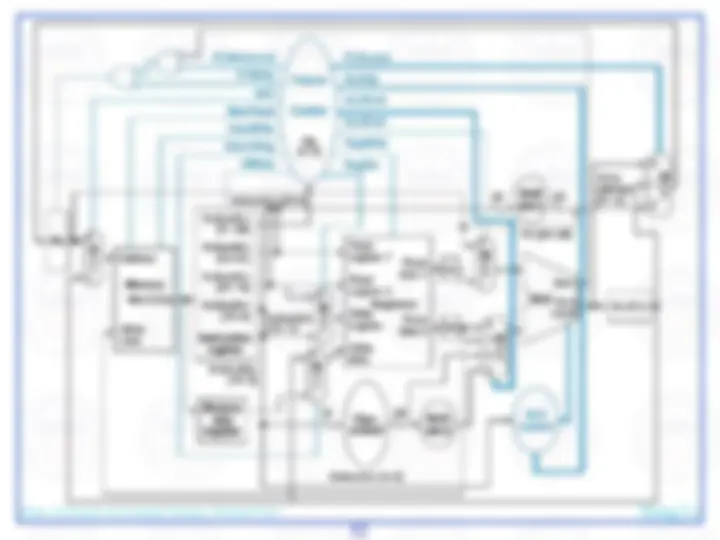
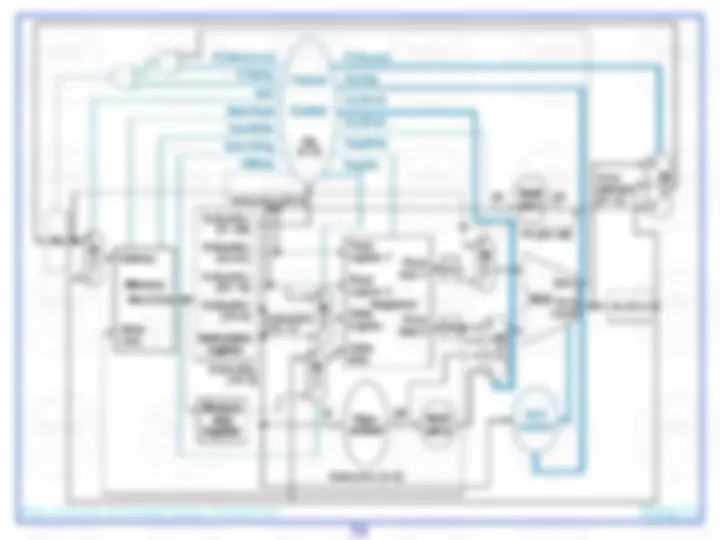
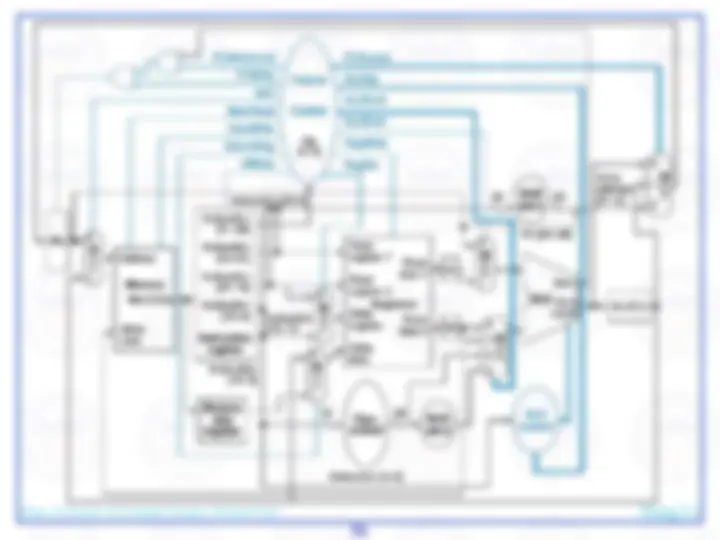
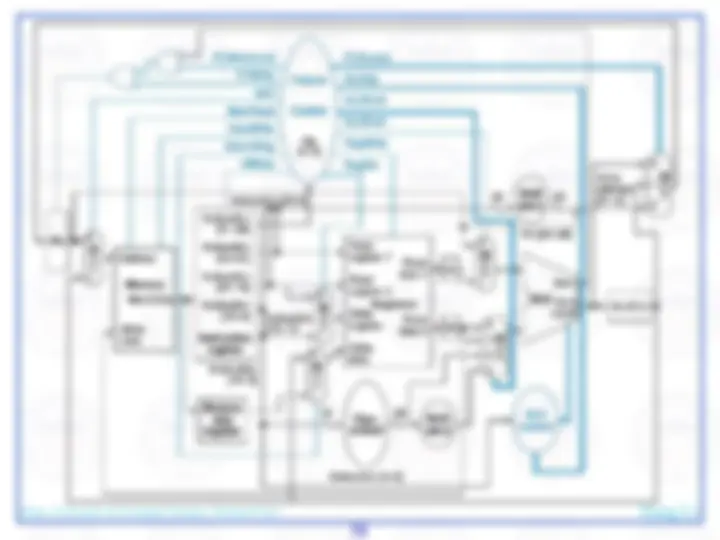
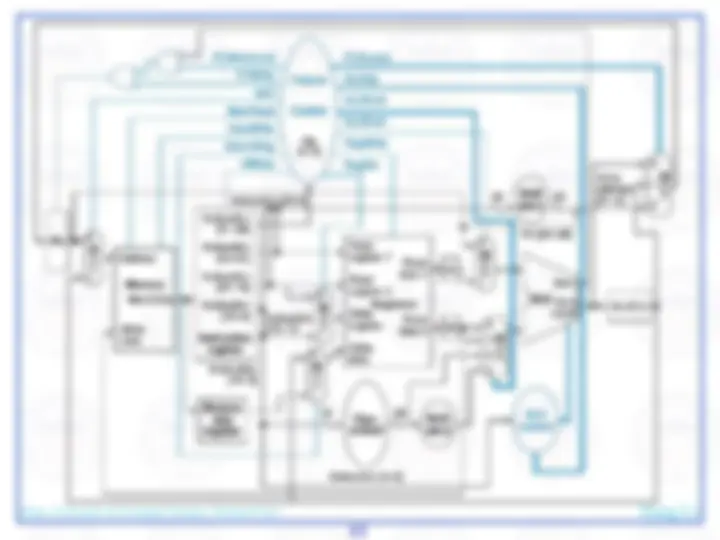
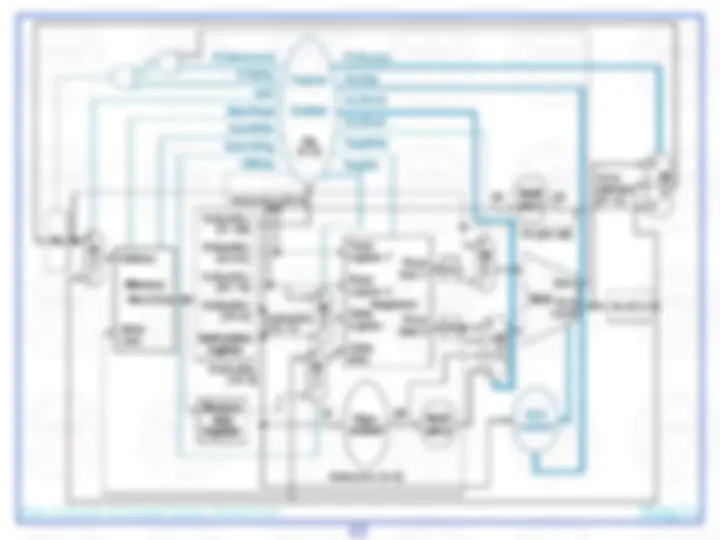
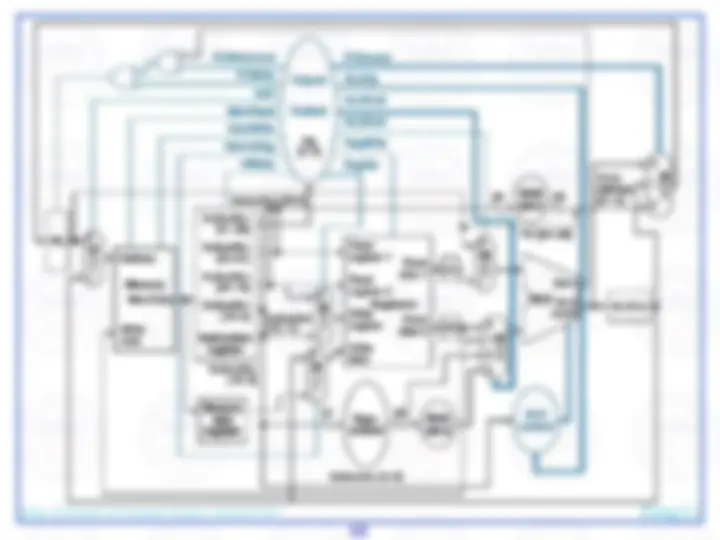
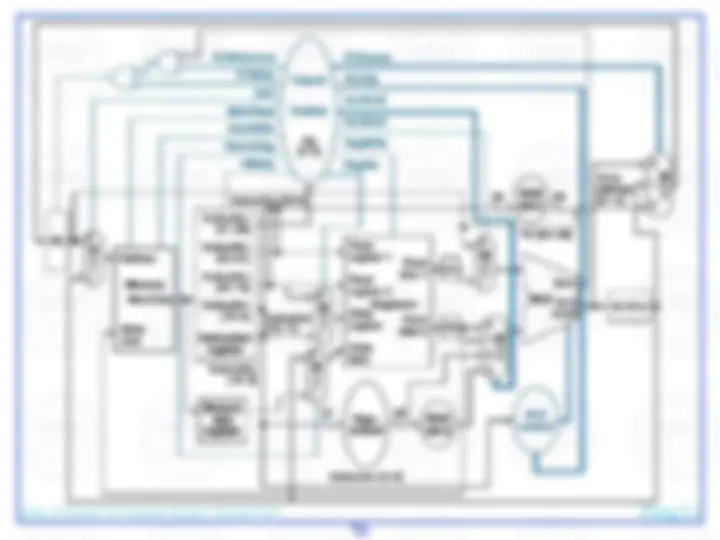
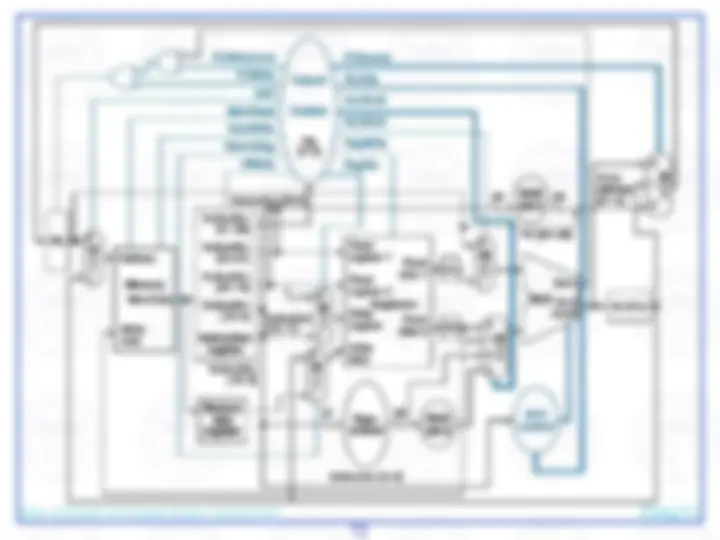
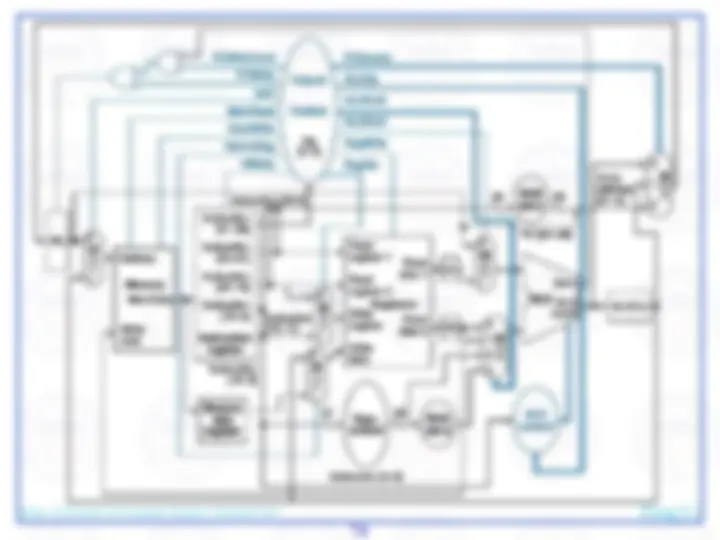
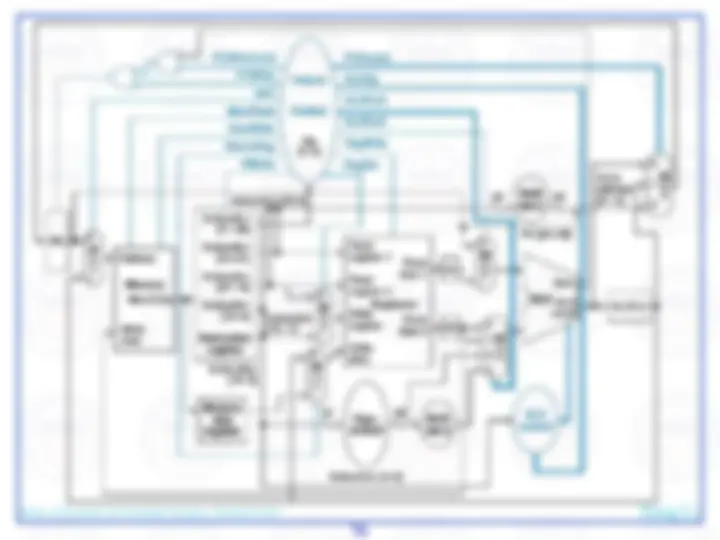
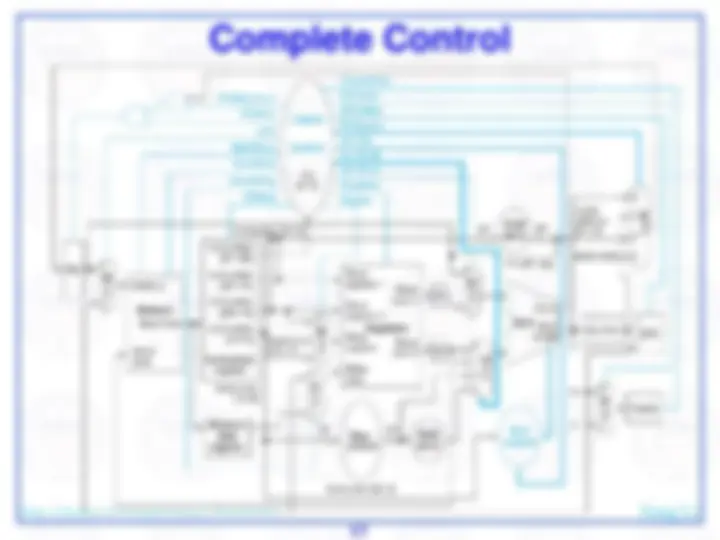
 Here's an abstract view of the basic architecture needed to implement our subset of the MIPS environment:

We will first examine the problem of fetching instructions and updating the address in the program counter, common for the execution of all instructions.

Dept. of Systems & Computer Science, Howard Univ. Jiang Li

Fetching Instructions

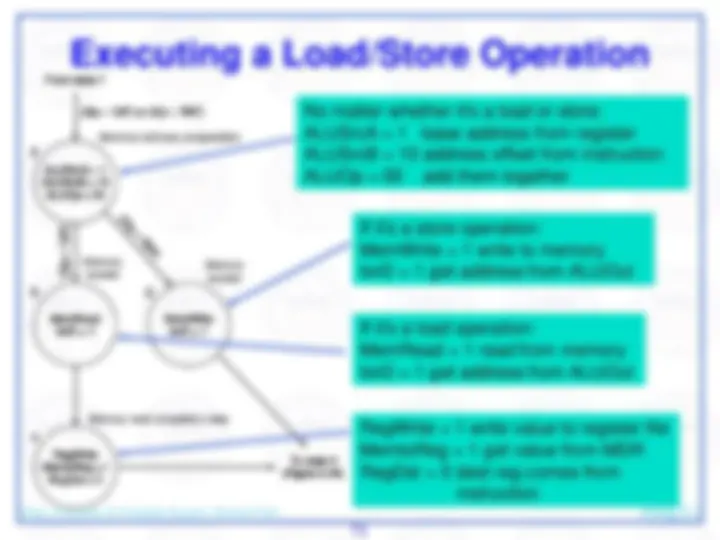
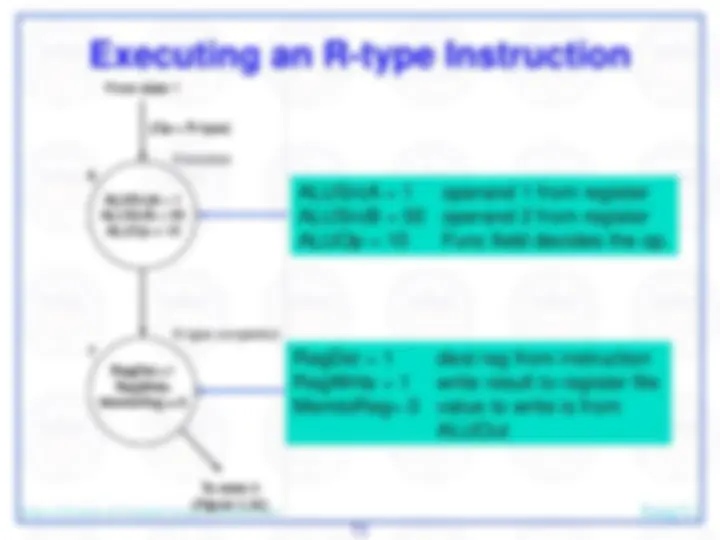
 The basic steps are to send the address in the program counter (PC) to the instruction memory, obtain the specified instruction, and increment the value in the PC.  For now, we assume sequential execution.  Eventually the instruction memory will need write facilities (to load programs), but we ignore that for now.  For now, the adder need only add the MIPS word size to the PC to prepare for loading the next instruction.  The fetched instruction will be used by other portions of the datapath…

Dept. of Systems & Computer Science, Howard Univ. Jiang Li

Branch Instructions

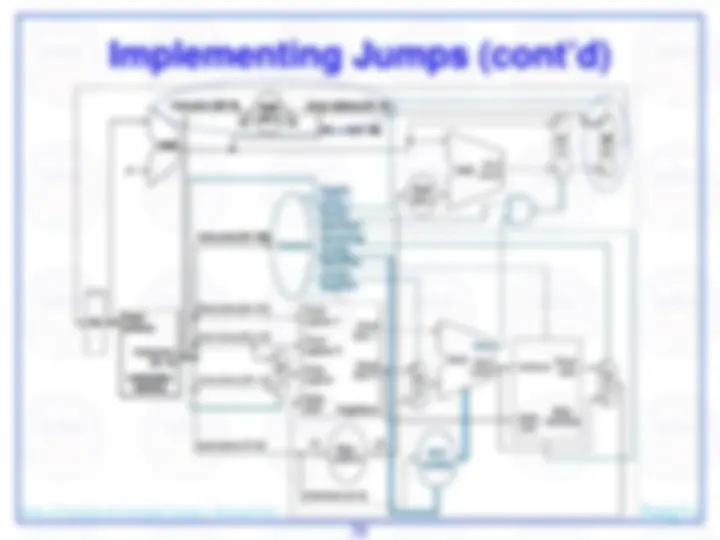
register file contains the 32 registers

adder computes target address for branch

ALU evaluates beq test

sign-extension for 16-bit address from instruction

control logic selects appropriate value for updating PC

Dept. of Systems & Computer Science, Howard Univ. Jiang Li

A Simple Unified Datapath

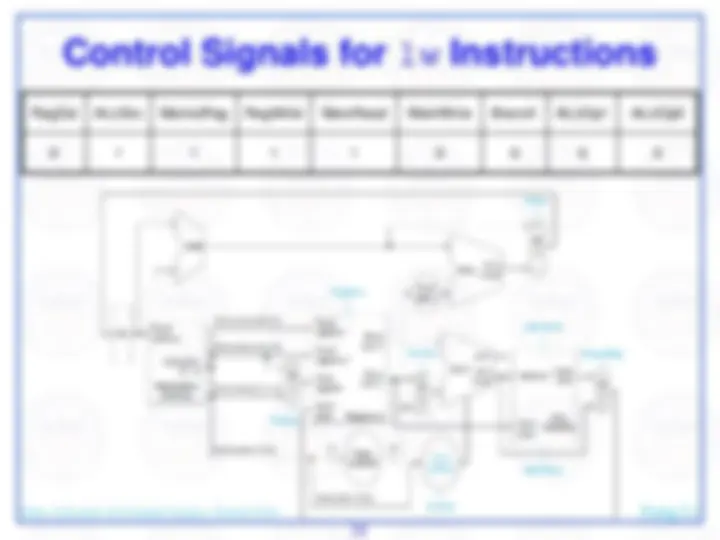
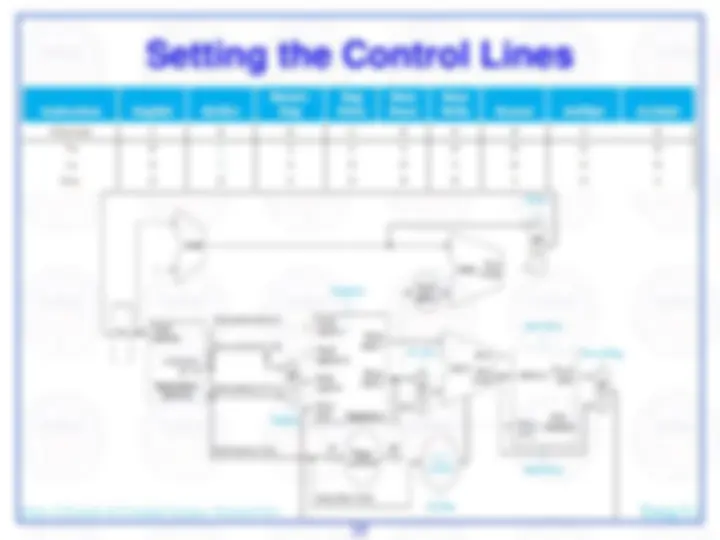
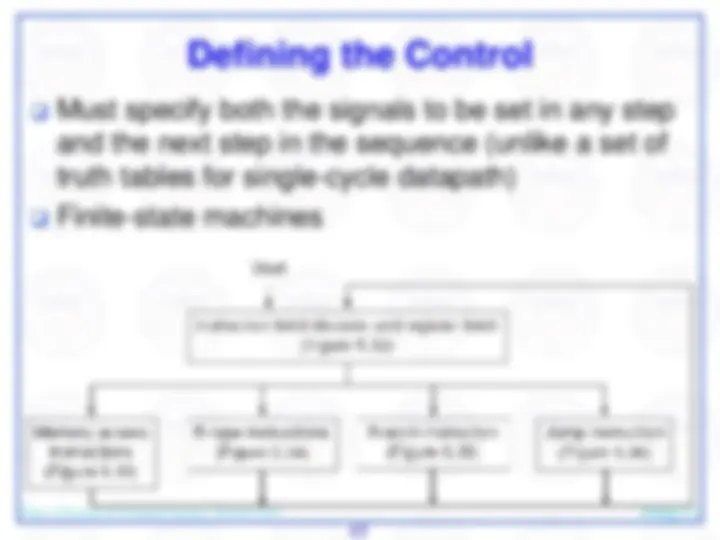
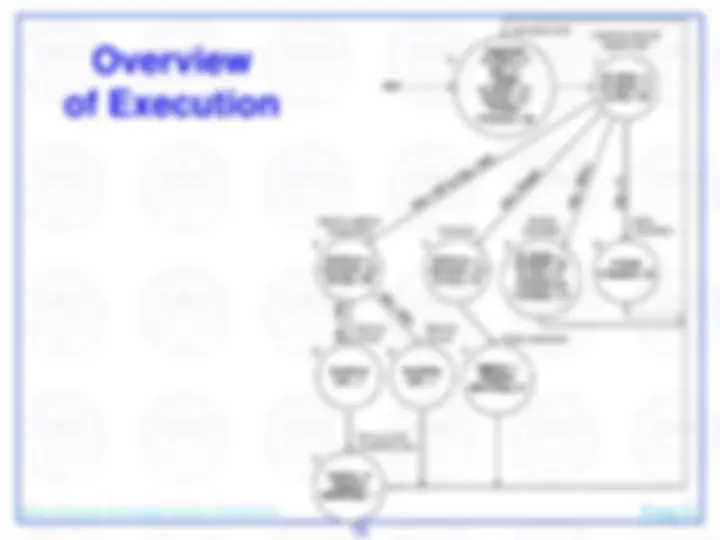
We assume each instruction can be completed during a single clock cycle… that will be addressed later…

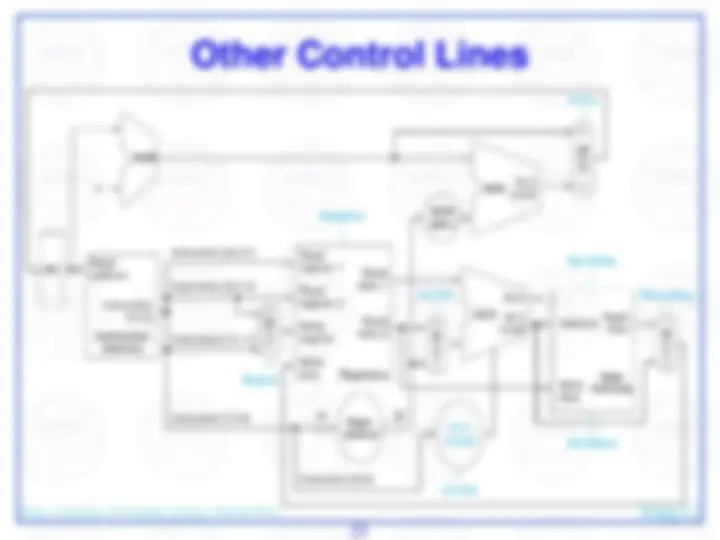
mux chooses correct address to update PC

Dept. of Systems & Computer Science, Howard Univ. Jiang Li

Datapath Control Details

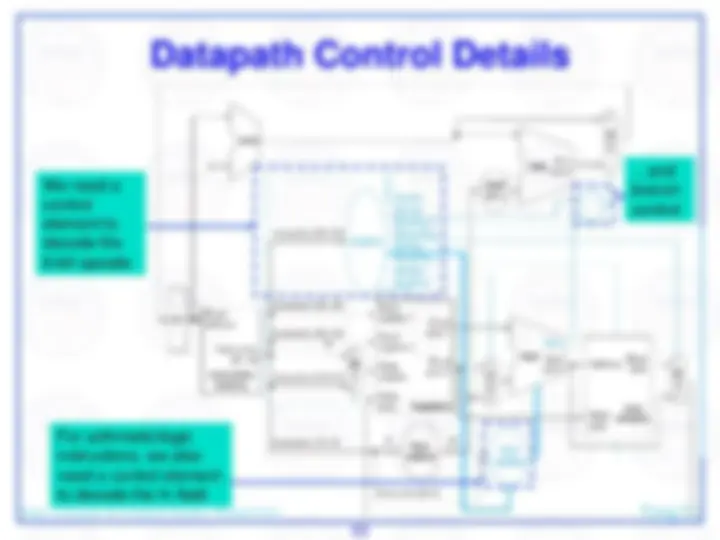
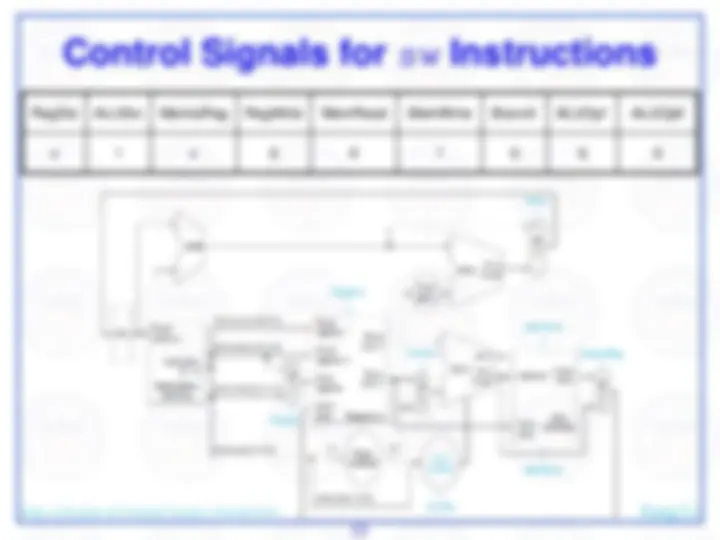
We need a control element to decode the 6-bit opcode

For arithmetic/logic instructions, we also need a control element to decode the fn field

…and branch control

Dept. of Systems & Computer Science, Howard Univ. Jiang Li

The ALU Control

 ALU has 4 control inputs  Only 6 combinations are used

Not used in our discussion

Dept. of Systems & Computer Science, Howard Univ. Jiang Li

The ALU Control (cont’d)

 The truth table for the 4 ALU control bits (called Operation)

 What is the Boolean expression for Operation?

Dept. of Systems & Computer Science, Howard Univ. Jiang Li

Boolean Algebra Review (1)

 A Boolean algebra is a set B of values together with:  Two binary operations, usually denoted by + and · ,  A unary operation, usually denoted by ¯,  Two elements usually called zero and one  … such that certain axioms are satisfied:  Associativity of each binary operation over the other,  Commutativity of each each binary operation,  Distributivity of each binary operation over the other,  Absorption rules,  Existence of complements with respect to each binary operation

Dept. of Systems & Computer Science, Howard Univ. Jiang Li

Boolean Algebra Review (3)

 Absorption Laws : for all a , b and c in B , a + (a ⋅ b) = a a ⋅ (a + b) = a  Existence of Complements : for all a in B , there exists an element ā in B such that a + ā = 1 a ⋅ ā = 0

Dept. of Systems & Computer Science, Howard Univ. Jiang Li

De Morgan's Laws & More

 De Morgan's Laws are useful theorems that can be derived from the fundamental properties of a Boolean algebra.

 Double-negation law :

For all a and b in B , a + b = a ⋅ b a ⋅ b = a + b

a = a

Dept. of Systems & Computer Science, Howard Univ. Jiang Li

Boolean Expressions and Equations

 A Boolean expression is defined in terms of the three basic Boolean operators and variables which may take on the values 0 and 1. For example:

 A Boolean equation is an assertion that two Boolean expression are equal , where equal means that the values of the two expressions are the same for all possible assignments of values to their variables. For example:

1 2 1 2 3 1 2 3

0 0 0 0 y x x x x x x x x

z x y x y

⋅ + ⋅ ⋅ + ⋅ +

x 0 (^) ⋅ y 0 + x 0 ⋅ y 0 = ( x 0 + y 0 )⋅( x 0 + y 0 )

Dept. of Systems & Computer Science, Howard Univ. Jiang Li

Example: Truth Table → Boolean Exp.

 Sum is 1 for A ⋅ B and A ⋅ B

Sum = A ⋅ B + A ⋅ B