The Method of Sections: Determining Forces in Truss Members, Study Guides, Projects, Research of Engineering

Download The Method of Sections: Determining Forces in Truss Members and more Study Guides, Projects, Research Engineering in PDF only on Docsity!

Lecture 20

ENGR-1100 Introduction to

Engineering Analysis

THE METHOD OF SECTIONS

In-Class Activities :

• (^) Reading Quiz
• (^) Applications
• (^) Method of Sections
• (^) Concept Quiz
• (^) Group Problem Solving
• (^) Attention Quiz Today’s Objectives : Students will be able to determine:

1. Forces in truss members using the method of sections.

THE METHOD OF SECTIONS

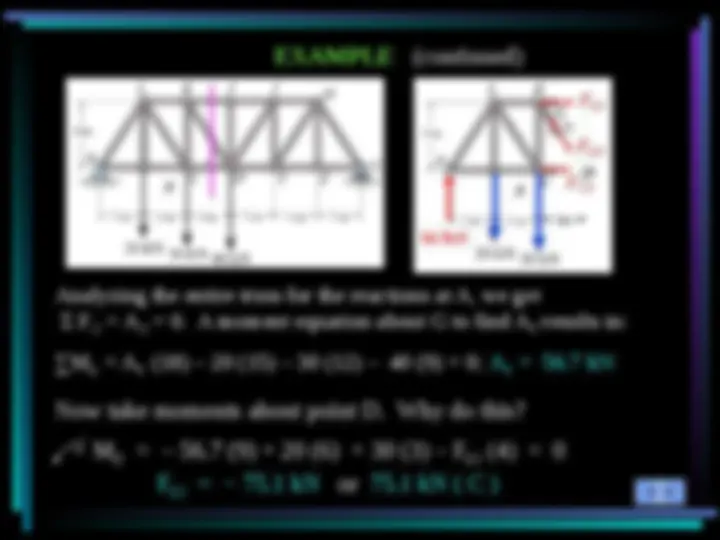
In the method of sections, a truss is divided into two parts by taking an imaginary “cut” (shown here as a-a) through the truss. Since truss members are subjected to only tensile or compressive forces along their length, the internal forces at the cut members will also be either tensile or compressive with the same magnitude as the forces at the joint. This result is based on the equilibrium principle and Newton’s third law.

STEPS FOR ANALYSIS

1. Decide how you need to “cut” the truss. This is based on: a) where you need to determine forces, and, b) where the total number of unknowns does not exceed three (in general).
2. Decide which side of the cut truss will be easier to work with (minimize the number of external reactions).
3. If required, determine any necessary support reactions by drawing the FBD of the entire truss and applying the E-of-E.

5. Apply the scalar equations of equilibrium (E-of-E) to the selected cut section of the truss to solve for the unknown member forces. Please note, in most cases it is possible to write one equation to solve for one unknown directly. So look for it and take advantage of such a shortcut! STEPS FOR ANALYSIS (continued)

EXAMPLE

a) Take a cut through members KJ, KD and CD. b) Work with the left part of the cut section. Why? c) Determine the support reactions at A. What are they? d) Apply the E-of-E to find the forces in KJ, KD and CD. Given : Loads as shown on the truss. Find : The force in members KJ, KD, and CD. Plan:

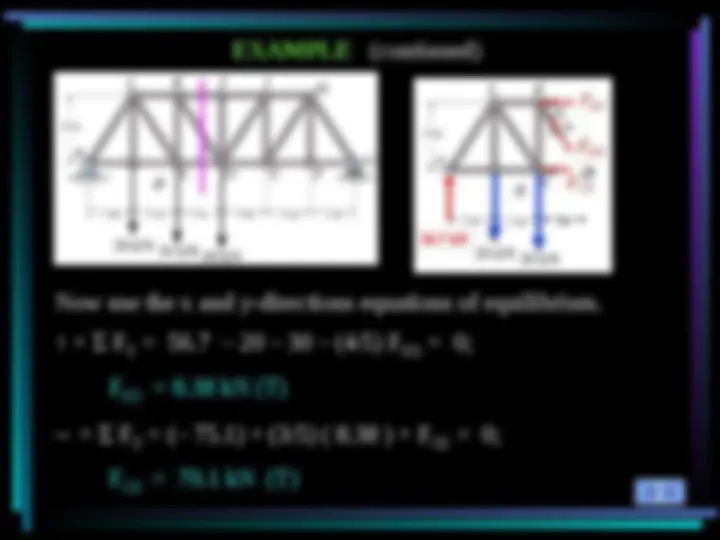
EXAMPLE (continued) Now use the x and y-directions equations of equilibrium. ↑ +  F Y

= 56.7 – 20 – 30 – (4/5) F

KD

F

KD = 8.38 kN (T) → +  F X

= (– 75.1) + (3/5) ( 8.38 ) + F

CD

F

CD = 70.1 kN (T) 56.7 kN

READING QUIZ

1. In the method of sections, generally a “cut” passes through no more than _____ members in which the forces are unknown. A) 1 B) 2 C) 3 D) 4
2. If a simple truss member carries a tensile force of T along its length, then the internal force in the member is ______. A) Tensile with magnitude of T/ B) Compressive with magnitude of T/ C) Compressive with magnitude of T D) Tensile with magnitude of T

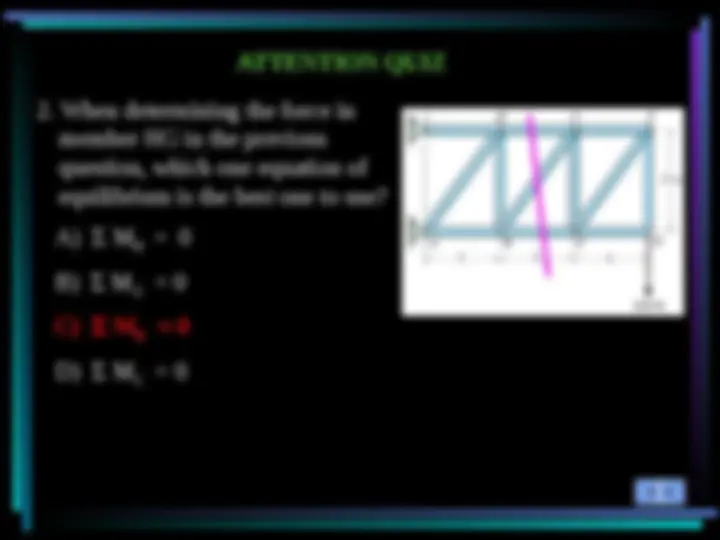
CONCEPT QUIZ (continued)

2. If you know F ED , how will you determine F EB

A) By taking section b-b and using  M E

B) By taking section b-b, and using  F X = 0 and  F Y

C) By taking section a-a and using  M B

D) By taking section a-a and using  M D

ATTENTION QUIZ

1. As shown, a cut is made through members GH, BG and BC to determine the forces in them. Which section will you choose for analysis and why? A) Right, fewer calculations. B) Left, fewer calculations. C) Either right or left, same amount of work. D) None of the above, too many unknowns.

GROUP PROBLEM SOLVING

a) Take the cut through members GF, GB and AB. b) Analyze the left section. Determine the support reactions at A. Why? c) Draw the FBD of the left section. d) Apply the equations of equilibrium (if possible, try to do it so that every equation yields an answer to one unknown. Given : Loads as shown on the truss. Find : The force in members GB and GF. Plan:

GROUP PROBLEM SOLVING (continued)

1. Determine the support reactions at A by drawing the FBD of the entire truss. +→  F X

= A

X

+  M

D

= – A

Y

A

Y = 671.4 lb Why is A x equal zero by inspection?