






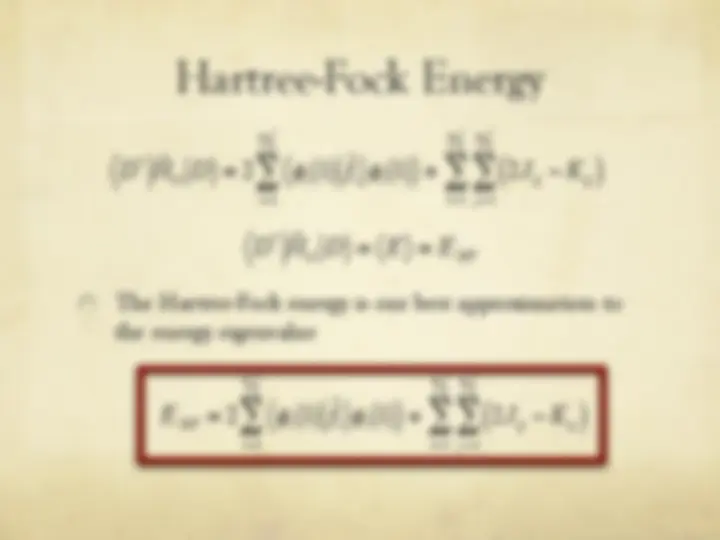








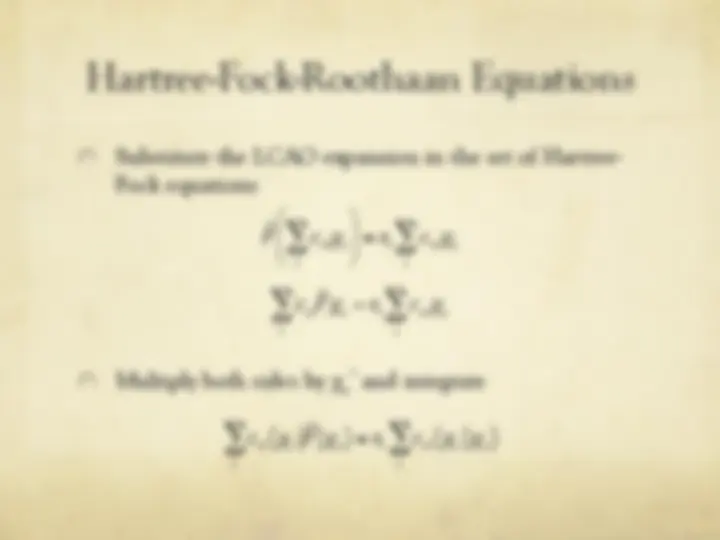



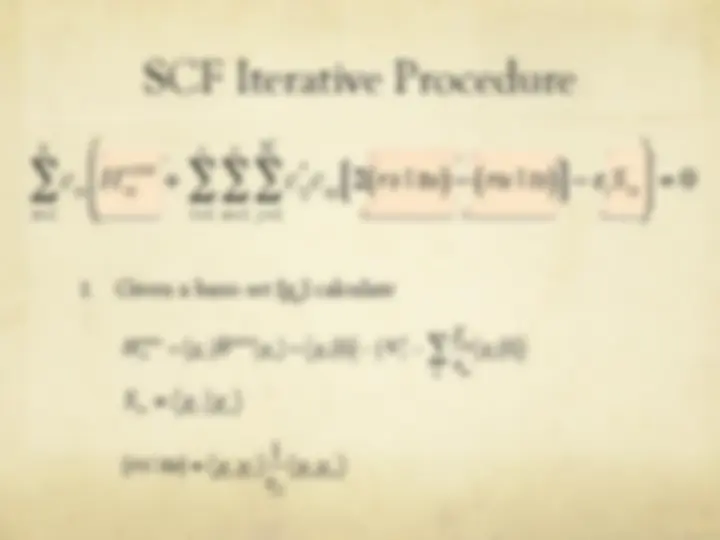






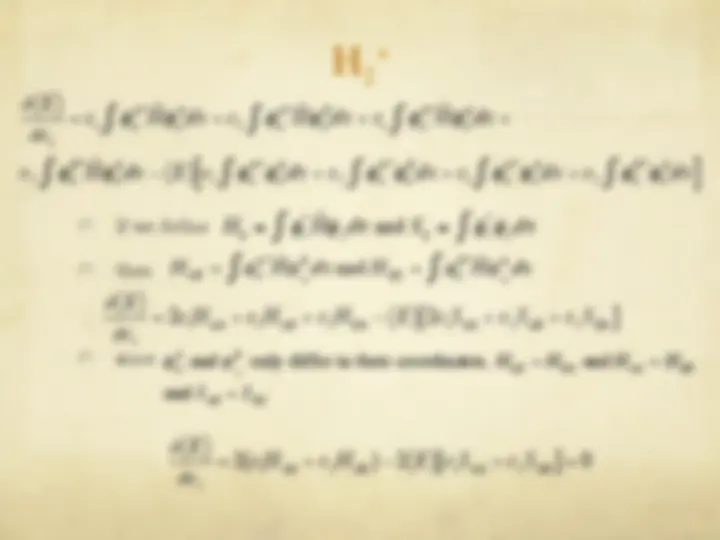
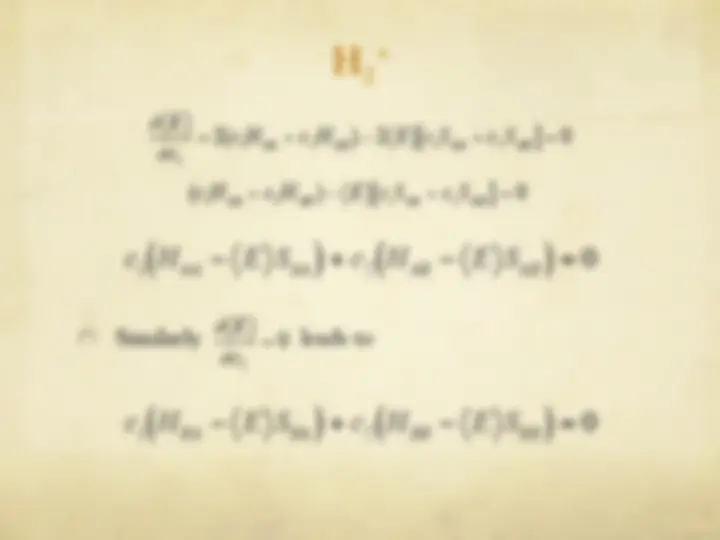
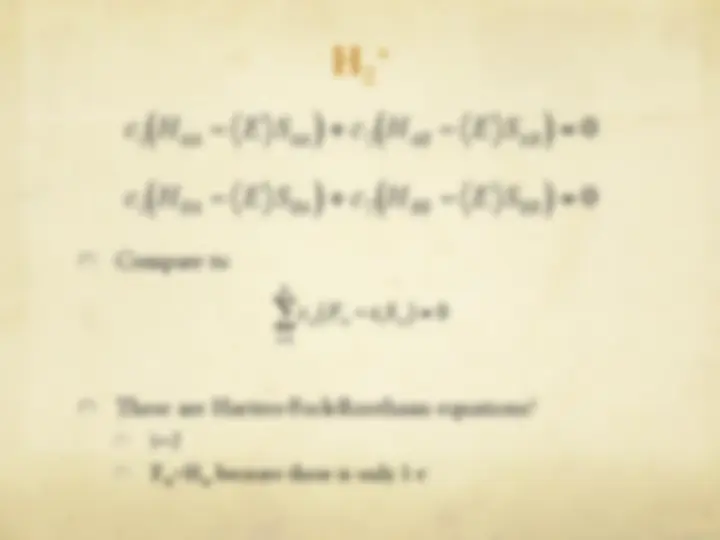
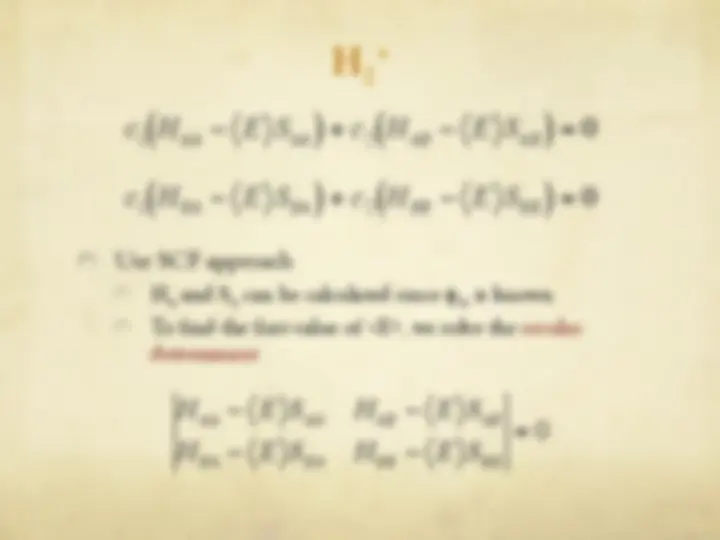



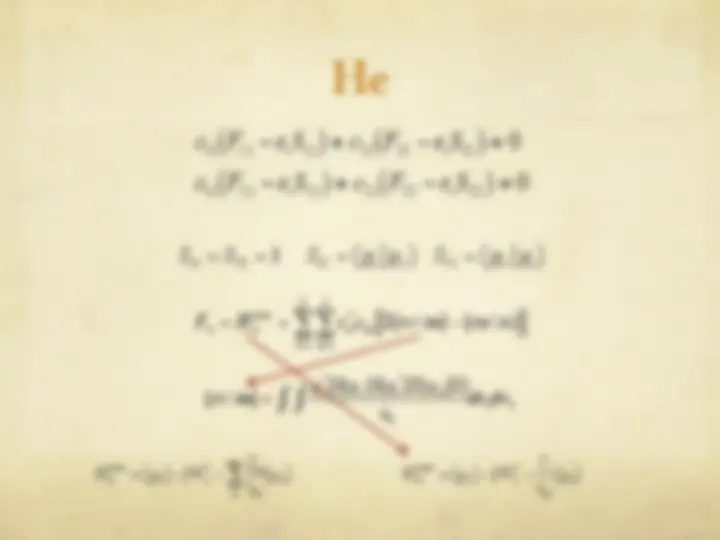








Study with the several resources on Docsity

Earn points by helping other students or get them with a premium plan


Prepare for your exams
Study with the several resources on Docsity

Earn points to download
Earn points by helping other students or get them with a premium plan
Community
Ask the community for help and clear up your study doubts
Discover the best universities in your country according to Docsity users
Free resources
Download our free guides on studying techniques, anxiety management strategies, and thesis advice from Docsity tutors
Hartree-Fock Energy and Equations, Self-Consistent-Field Procedure.
Typology: Lecture notes
1 / 53

This page cannot be seen from the preview
Don't miss anything!







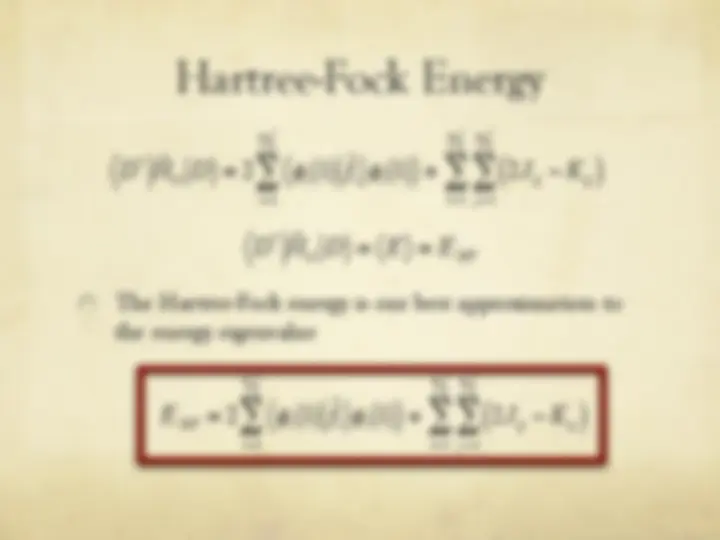








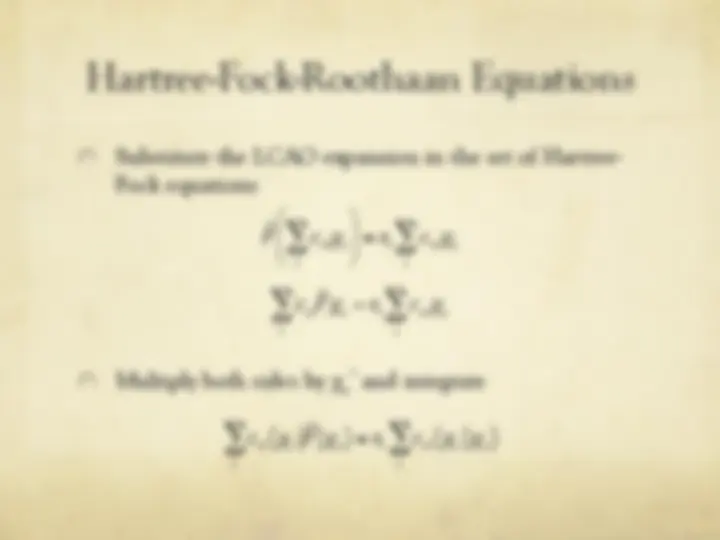



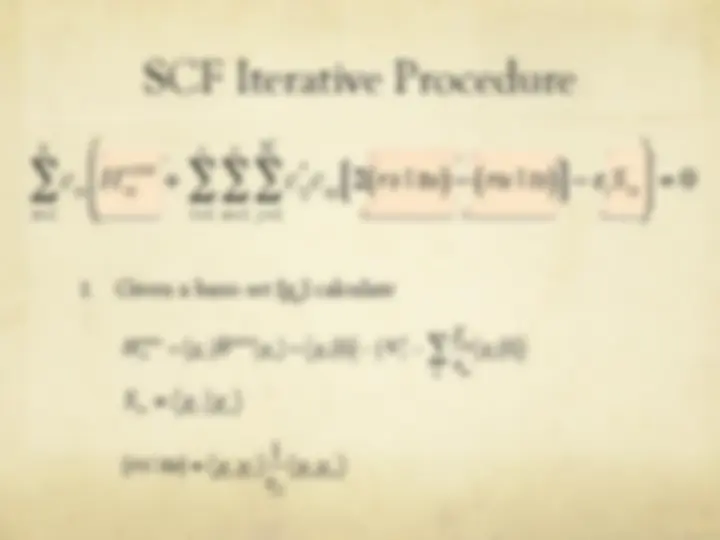







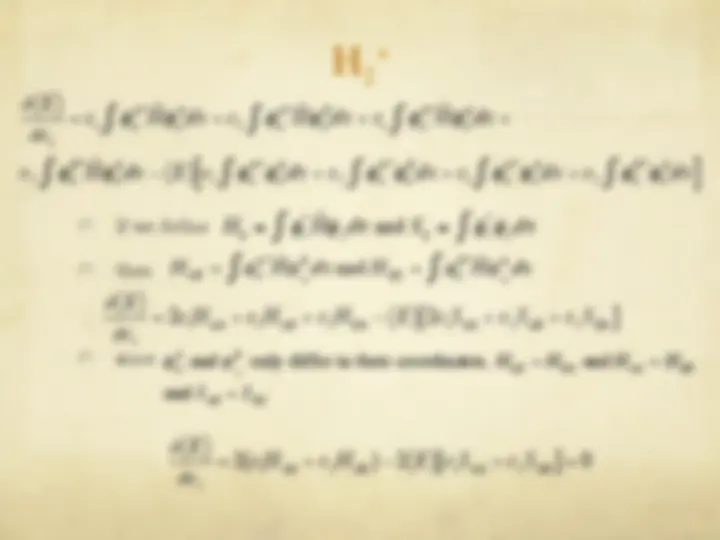
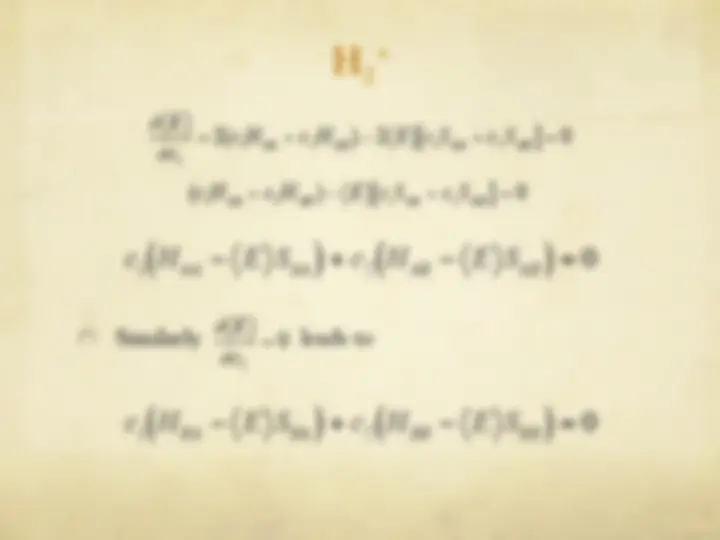
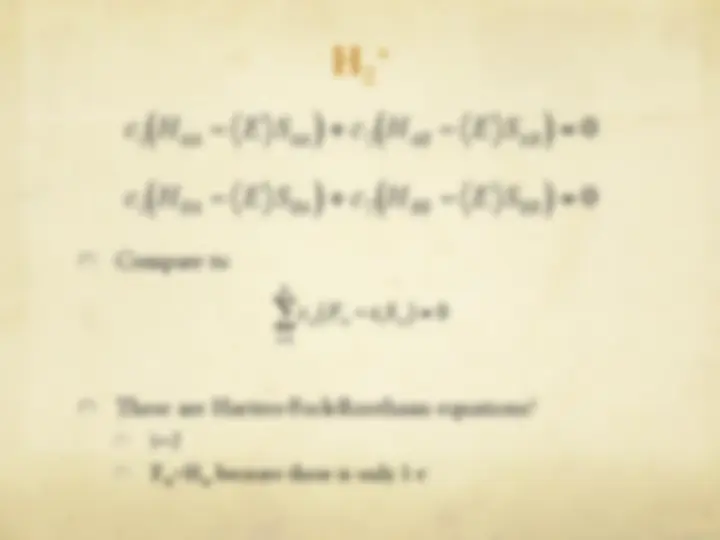
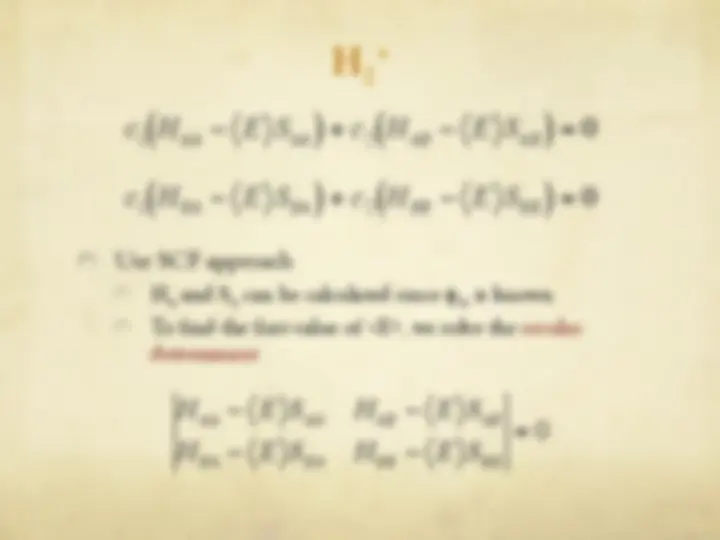



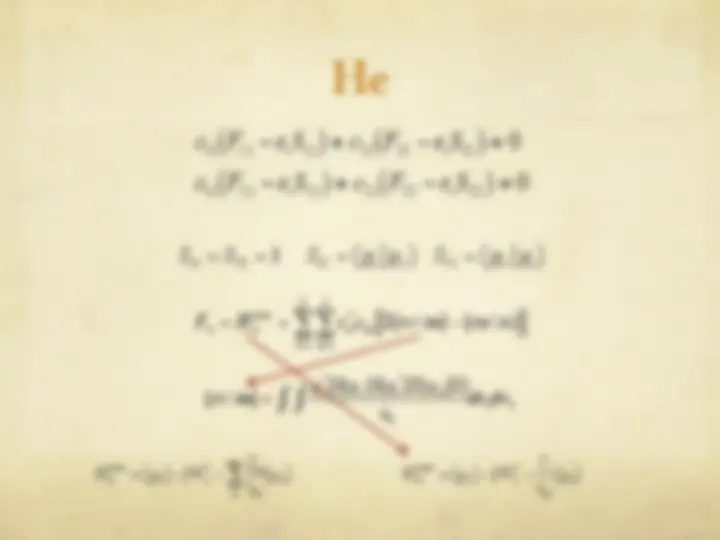






Chem 561
Lecture Outline
a) Coulomb and exchange integrals
a) The LCAO Approximation
a) H 2
b) He
" Recall the electronic Hamiltonian for molecules
" Define
€
ˆ H el
= −
1
2
∇ i
2
i
−
Z α
r i i^ α
α
1
r i > j ij
j
€
ˆ f i
= −
1
2
∇ i
2 −
Z α
r α i^ α
g^ ˆ ij
r ij
el
i
i
ij
i > j
j
one-electron operator two-electron operator
" No analytical solution to this differential equation
where
" Use a trial-and-error, iterative approach
el
el
el
el
el
i
i
ij
i > j
j
" searching for a Slater determinant of spin orbitals (D)
that minimizes the variational integral
" Since D is normalized
€
W =
D
ˆ H el
Dd τ
D
Dd τ
€
W = D
ˆ H el
Dd τ
= D
ˆ H el
D
€
u i (^1 ) u^ j (^1 ) =^ δ ij
" according to the previous definition
el
f i
i
g ˆ ij
i > j
i
€
ˆ H el =
ˆ f i
i
g ˆ ij
i > j
j
" cross terms disappear because of orthonormality
f 1
i
f 1
i
i
f i
i
g ˆ ij
i > j
i
i and j label electrons
i labels spin orbitals
D
g ˆ 12
D = φ i
j
12
φ i
j
i
j
12
φ j
i
i > j
i
i and j label spin orbitals from Slater determinant
Coulomb and Exchange Integrals
" Define
D
g ˆ 12
D = φ i
(^1 )^ φ^ j
(^2 ) g ˆ 12
φ i
(^1 )φ^ j
(^2 ) −^ φ i
(^1 )φ^ j
(^2 ) g ˆ 12
φ j
(^1 )^ φ i
(^2 ) [ ]
i > j
∑
i
∑
€
J ij
= φ i (^1 )φ^ j (^2 )
1
r 12
φ i (^1 )^ φ^ j (^2 )
K ij
= φ i (^1 )^ φ^ j (^2 )
1
r 12
φ j (^1 )^ φ i (^2 )
Coulomb integral
Exchange integral
€
g^ ˆ ij
=
1
r ij
" The Hartree-Fock energy is our best approximation to
the energy eigenvalue
ˆ H el
i
f 1
i
i = 1
n 2
ij
j = 1
n 2
i = 1
n 2
ˆ H el
HF
HF
i
f 1
i
i = 1
n 2
j = 1
n 2
i = 1
n 2
" English mathematician and
physicist (1897-1958)
" used numerical analysis to
solve differential equations
for the calculation of atomic
wavefunctions
" the Hartree unit of energy is
named after him
HF
i
f 1
i
i = 1
n 2
j = 1
n 2
i = 1
n 2
€
J ij
= φ i (^1 )φ^ j (^2 )
1
r 12
φ i (^1 )φ^ j (^2 )
€
K ij
= φ i
j
1
r 12
φ j
i
Coulomb integral
Exchange integral
Coulombic (electrostatic)
interaction between two electrons
A nonclassical interaction
J ij
=J ji
K ij
=K ji
J ii
=K ii
" Define
the one-electron core Hamiltonian
HF
i
f 1
i
i = 1
n 2
j = 1
n 2
i = 1
n 2
core
f 1
and H ii
core
i
f 1
i
HF
ii
core
i = 1
n 2
ij
j = 1
n 2
i = 1
n 2
NN
for a system of n electrons in n /2 occupied spin orbitals
The Hartree-Fock Equations
" The spin orbitals are an orthonormal set
" We are now ready to optimize with respect to each
variational parameter {c si
}
€
φ i
= c si
s = 1
b
∑^ χ s
€
φ i
j
ij
= c si
t = 1
b
∑
s = 1
b
∑ ctj^ χ i (^1 )^ χ^ j (^1 )
si
" We define
The Hartree-Fock Equations
€
ˆ F (^) ( (^1) ) =
ˆ H
core (^1 ) +^2
ˆ J j (^1 ) −^
ˆ K j (^1 ) [ ]
j = 1
n 2
∑
€
ˆ J j (^1 ) f^ (^1 ) ≡^ f^ (^1 )^ φ^ j (^2 ) ∫
(^2 )
r 12
dv 2
ˆ K j (^1 ) f^ (^1 ) ≡^ φ^ j (^1 )
φ j
(^2 ) f^ (^2 )
r 12
dv ∫ 2
Coulomb operator
exchange operator
Fock operator