MATH 203 Test 2 Review Solutions
1. (a) The average lifetime of Type 1 batteries is from 1.55 hours less to 0.86 hours more
than average lifetime of Type 2 batteries. (b) It is not conclusive which type of battery
has the longer average lifetime.
______________________________________________________________________________
2. (a) Re-write the interval as 0.024 โค p
2
โ p
1
โค 0.052 and say
The percentage of patients for whom Treatment B worsens the condition is from 2.4
percentage points higher to 5.2 percentage points higher than the percentage of patients
under Treatment A.
(Without re-writing the interval: The percentage of patients for whom Treatment A
worsens the condition is from 5.2 percentage points lower to 2.4 percentage points lower
than the percentage of patients under Treatment B.)
(b) It is clear that Treatment B has the higher percentage of patients with a worsening
of the condition.
______________________________________________________________________________
3. (a) Test H0: = 25 vs. Ha: < 25
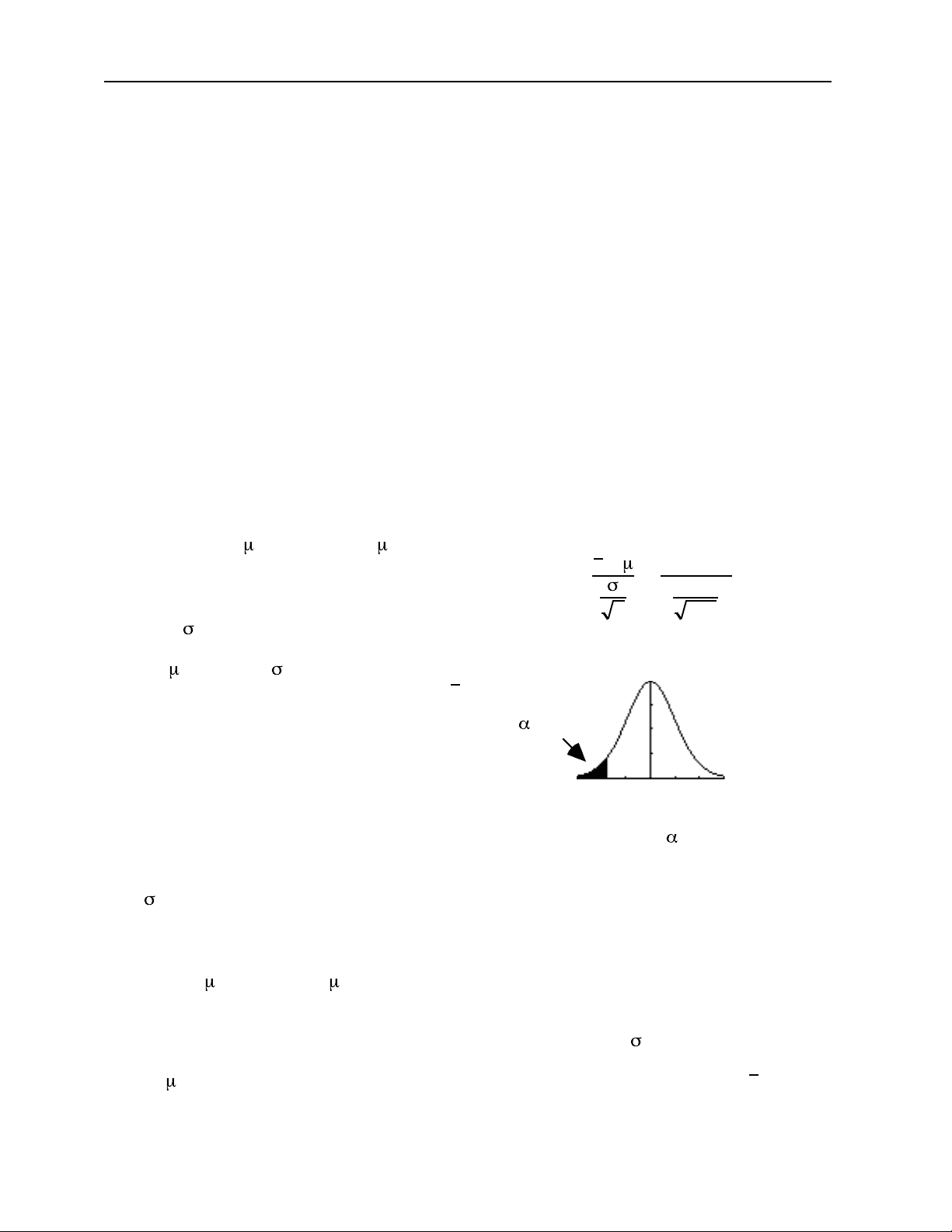
(b) We can use a ZโTest because the
measurement is normally distributed
and = 2 is known.
(c)
z
= x โ
n
= 24.2 โ25
2
400
= โ8
(d) If = 25 and = 2 were true, then
there would be no chance of getting an
x
of 24.2 or lower with a sample of 400 cars.
We can reject H0.
(f) Because we have a large sample, we can
still use the ZโTest even if the
measurement were not normally
distributed. Also, because of the large
sample, we can use
S
as an approximation
for and still use the ZโTest.
โ1.645
N(0, 1)
(e)
=0.05
curve
Use โ1.96 for
=0.025
.
โโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโ
4. (a) H0: = 6 vs. Ha: > 6 (b) With a small sample, we can use
the TโTest because the measurement
(birth weight) is normally distributed,
we do not know , but we have S.
(c) If = 6 were true, then there would be an 11.9% chance of getting an
x
of 6.3 or
higher with a sample of size 36. There is not enough evidence to reject H0.
