Download The Golden Ratio: Geometric Design and Calculation and more Assignments Mathematics in PDF only on Docsity!
Supplemental Section 2: The Golden Ratio
Practice HW (see WeBWorK problems) In the section, we look at the Golden Ratio , which is a number that can be used to design geometric objects that are pleasing to the eye. In this section, we denote the Golden Ratio by the Greek letter^ ^. It can be shown that the Golden Ratio is given by the following constant. Value of Golden Ratio 1. 62
The Golden Ratio for Lines
The Golden Ratio for lines is based upon the division of a line segment into two parts such that the ratio of the longer piece to the shorter piece is the same as the ratio of the entire line segment to the longer piece. Suppose we are given the following line segment. Then the Golden Ratio for lines says that 1. 62 a a b b a a b
Example 1: For the line of length 4 in, find a point that approximately divides each segment into the Golden Ratio. Solution: █
The Golden Rectangle
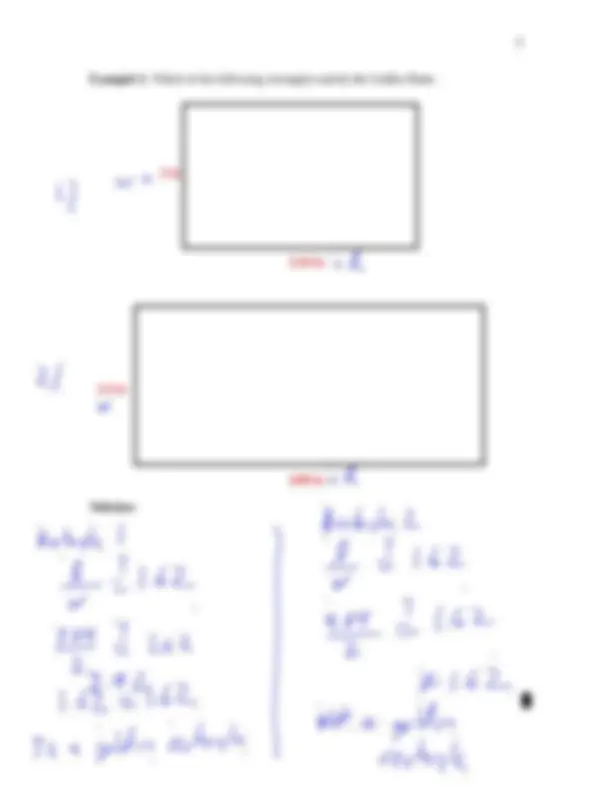
A Golden Rectangle is a rectangle whose sides from the Golden Ratio. If we are given the rectangle Then 1. 62 l l w w l l w
Example 3: Suppose one dimension of a Golden Rectangle is 9 in. Find the two possible values for the other dimension of the Golden Rectangle. Solution: █
The Golden Cross
To construct a "Golden Cross", you make the ratio of the height H to the width W equal to the Golden Ratio and the ratio of the bottom section of the cross B and the top section of the cross T equal to the Golden Ratio. Then, we have 1. 62 T B W H where B T H
Example 4: Find the width, bottom section, and top section of the cross (rounded to one digit to the right of the decimal place) if the height of the cross is H = 726 cm. Solution: █
Example 6: Find the width and height (rounded to one digit to the right of the decimal place) of the Golden Box if the length of the box is L = 536 cm. Solution: █
