Suma de Vectores por método analítico, Exercises of Law

Download Suma de Vectores por método analítico and more Exercises Law in PDF only on Docsity!

“Suma de Vectores por el Método

Analítico”

Agosto del 2023

Universidad Autónoma Chapingo

Dpto. de Preparatoria Agrícola

Área de Física

A menudo se presentan vectores expresados en coordenadas polares y tenemos necesidad de obtener la resultante de esos vectores al estar aplicados a un punto. Presentamos a continuación un método para sumar vectores expresados en forma polar. El método consiste en tres pasos: 1 .- Cuando tenemos un conjunto de vectores expresados en forma polar, es necesario expresarlos en forma cartesiana para poderlos sumar. Las ecuaciones de transformación son las siguientes:

𝑥 = 𝑉 𝑐𝑜𝑠 𝜃 y 𝑦 = 𝑉 𝑠𝑒𝑛𝜃

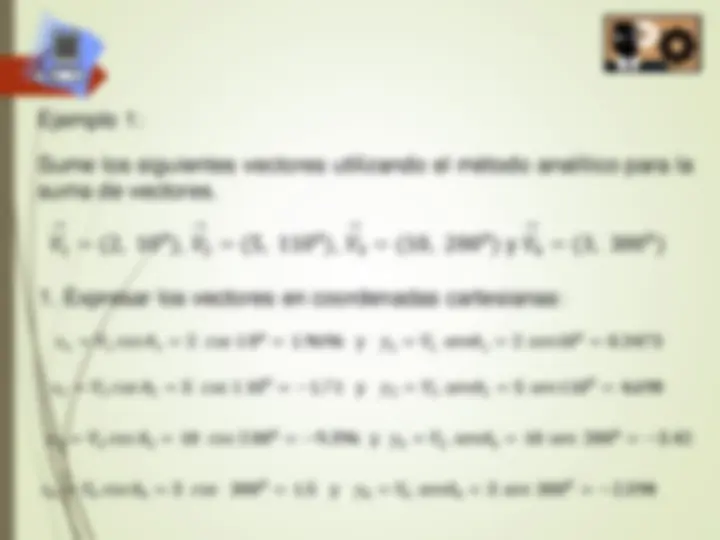
Ejemplo 1 : Sume los siguientes vectores utilizando el método analítico para la suma de vectores. 𝑉 → 1 =^ (^2 ,^10 0 ), 𝑉 → 2 =^ (^5 ,^110 0 ), 𝑉 → 3 =^ (^10 ,^200 0 ) y 𝑉 → 4 =^ (^3 ,^300 0 )

1. Expresar los vectores en coordenadas cartesianas: 𝑥 1 = 𝑉 1 𝑐𝑜𝑠 𝜃 1 = 2 𝑐𝑜𝑠 1 0 0 = 1. 9696 y 𝑦 1 = 𝑉 1 𝑠𝑒𝑛𝜃 1 = 2 𝑠𝑒𝑛1 0 0 = 0. 3473 𝑥 2 = 𝑉 2 𝑐𝑜𝑠 𝜃 2 = 5 𝑐𝑜𝑠 1 10 0 = − 1. 71 y 𝑦 2 = 𝑉 2 𝑠𝑒𝑛𝜃 2 = 5 𝑠𝑒𝑛 110 0 = 4. 698 𝑥 3 = 𝑉 3 𝑐𝑜𝑠 𝜃 3 = 10 𝑐𝑜𝑠 2 00 0 = − 9. 396 y 𝑦 3 = 𝑉 3 𝑠𝑒𝑛𝜃 3 = 10 𝑠𝑒𝑛 200 0 = − 3. 42 𝑥 4 = 𝑉 4 𝑐𝑜𝑠 𝜃 4 = 3 𝑐𝑜𝑠 300 0 = 1. 5 y 𝑦 4 = 𝑉 4 𝑠𝑒𝑛𝜃 4 = 3 𝑠𝑒𝑛 300 0 = − 2. 598

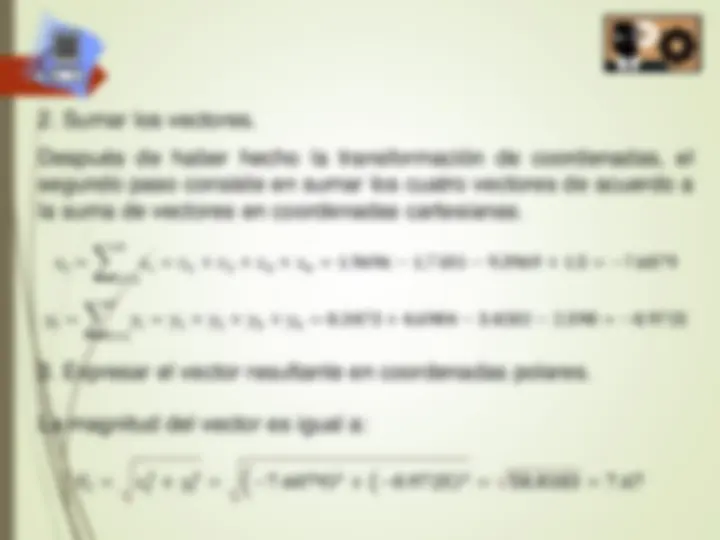
2. Sumar los vectores. Después de haber hecho la transformación de coordenadas, el segundo paso consiste en sumar los cuatro vectores de acuerdo a la suma de vectores en coordenadas cartesianas. 𝑥𝑡 = ෍ 𝑖= 1 𝑛 𝑥𝑖 = 𝑥 1 + 𝑥 2 + 𝑥 3 + 𝑥 4 = 1. 9696 − 1. 7101 − 9. 3969 + 1. 5 = − 7. 6079 𝑦𝑡 = ෍ 𝑖= 1 𝑛 𝑦𝑖 = 𝑦 1 + 𝑦 2 + 𝑦 3 + 𝑦 4 = 0. 3473 + 4. 6984 − 3. 4202 − 2. 598 = − 0. 9725
3. Expresar el vector resultante en coordenadas polares. La magnitud del vector es igual a: 𝑉𝑡 = 𝑥𝑡 2

• 𝑦𝑡 2 = ቀ − 7. 6079 ) 2
• ൫ − 0. 9725 ) 2 = 58. 8183 = 7. 67

Ejemplo 2 : Sume los siguientes vectores utilizando el método analítico para la suma de vectores.

1. Expresar los vectores en coordenadas cartesianas:

→ 1 =^ (^4 ,^45 0 ), 𝑉 → 2 =^ (^2 ,^160 0 ) y 𝑉 → 3 =^ (^1 ,^310 0 ). 𝑥 1 = 𝑉 1 𝑐𝑜𝑠 𝜃 1 = 4 𝑐𝑜𝑠 4 5 0 = 2. 828 y 𝑦 1 = 𝑉 1 𝑠𝑒𝑛𝜃 1 = 4 𝑠𝑒𝑛 45 0 = 2. 828 𝑥 2 = 𝑉 2 𝑐𝑜𝑠 𝜃 2 = 2 𝑐𝑜𝑠 160 0 = − 1. 879 y 𝑦 2 = 𝑉 2 𝑠𝑒𝑛𝜃 2 = 2 𝑠𝑒𝑛 160 0 = 0. 684 𝑥 3 = 𝑉 3 𝑐𝑜𝑠 𝜃 3 = 1 𝑐𝑜𝑠 310 0 = 0. 6428 y 𝑦 3 = 𝑉 3 𝑠𝑒𝑛𝜃 3 = 1 𝑠𝑒𝑛 310 0 = − 0. 766

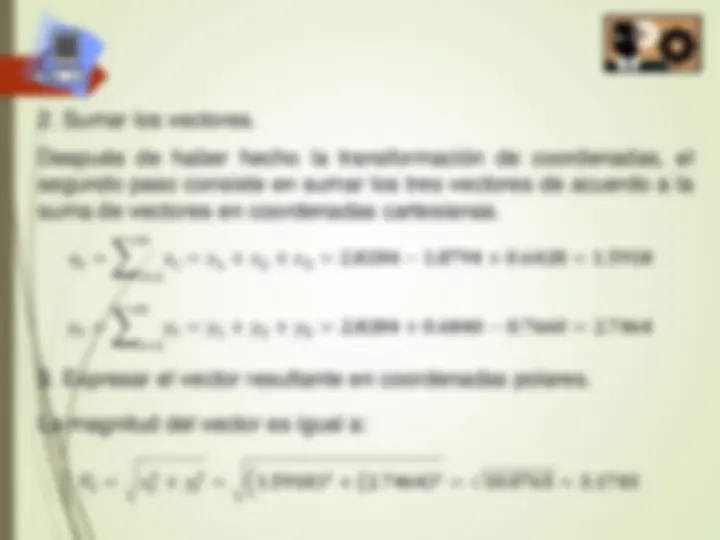
2. Sumar los vectores. Después de haber hecho la transformación de coordenadas, el segundo paso consiste en sumar los tres vectores de acuerdo a la suma de vectores en coordenadas cartesianas.
3. Expresar el vector resultante en coordenadas polares. La magnitud del vector es igual a: 𝑥𝑡 = ෍ 𝑖= 1 𝑛 𝑥𝑖 = 𝑥 1 + 𝑥 2 + 𝑥 3 = 2. 8284 − 1. 8794 + 0. 6428 = 1. 5918 𝑦𝑡 = ෍ 𝑖= 1 𝑛 𝑦𝑖 = 𝑦 1 + 𝑦 2 + 𝑦 3 = 2. 8284 + 0. 6840 − 0. 7660 = 2. 7464 𝑉𝑡 = 𝑥𝑡 2

• 𝑦𝑡 2 = ቀ 1. 5918 ) 2
• ൫ 2. 7464 ) 2 = 10. 0765 = 3. 1743

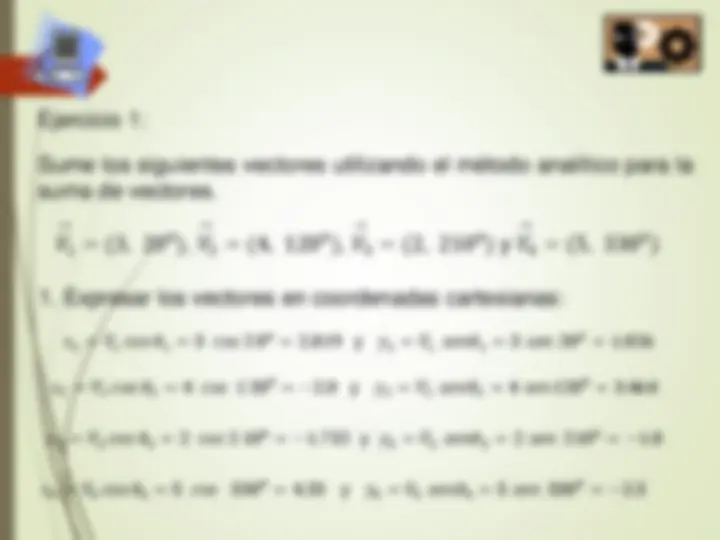
Ejercicio 1 : Sume los siguientes vectores utilizando el método analítico para la suma de vectores. 𝑉 → 1 =^ (^3 ,^20 0 ), 𝑉 → 2 =^ (^4 ,^120 0 ), 𝑉 → 3 =^ (^2 ,^210 0 ) y 𝑉 → 4 =^ (^5 ,^330 0 )

1. Expresar los vectores en coordenadas cartesianas: 𝑥 1 = 𝑉 1 𝑐𝑜𝑠 𝜃 1 = 3 𝑐𝑜𝑠 2 0 0 = 2. 819 y 𝑦 1 = 𝑉 1 𝑠𝑒𝑛𝜃 1 = 3 𝑠𝑒𝑛 20 0 = 1. 026 𝑥 2 = 𝑉 2 𝑐𝑜𝑠 𝜃 2 = 4 𝑐𝑜𝑠 1 20 0 = − 2. 0 y 𝑦 2 = 𝑉 2 𝑠𝑒𝑛𝜃 2 = 4 𝑠𝑒𝑛 120 0 = 3. 464 𝑥 3 = 𝑉 3 𝑐𝑜𝑠 𝜃 3 = 2 𝑐𝑜𝑠 2 10 0 = − 1. 732 y 𝑦 3 = 𝑉 3 𝑠𝑒𝑛𝜃 3 = 2 𝑠𝑒𝑛 210 0 = − 1. 0 𝑥 4 = 𝑉 4 𝑐𝑜𝑠 𝜃 4 = 5 𝑐𝑜𝑠 330 0 = 4. 33 y 𝑦 4 = 𝑉 4 𝑠𝑒𝑛𝜃 4 = 5 𝑠𝑒𝑛 330 0 = − 2. 5

2. Sumar los vectores. Después de haber hecho la transformación de coordenadas, el segundo paso consiste en sumar los cuatro vectores de acuerdo a la suma de vectores en coordenadas cartesianas. 𝑥𝑡 = ෍ 𝑖= 1 𝑛 𝑥𝑖 = 𝑥 1 + 𝑥 2 + 𝑥 3 + 𝑥 4 = 2. 819 − 2. 0 − 1. 732 + 4. 33 = 3. 417 𝑦𝑡 = ෍ 𝑖= 1 𝑛 𝑦𝑖 = 𝑦 1 + 𝑦 2 + 𝑦 3 + 𝑦 4 = 1. 026 + 3. 464 − 1. 0 − 2. 5 = 0. 990
3. Expresar el vector resultante en coordenadas polares. La magnitud del vector es igual a: 𝑉𝑡 = 𝑥𝑡 2

• 𝑦𝑡 2 = ቀ 3. 417 ) 2
• ൫ 0. 990 ) 2 = 12. 657 = 3. 558

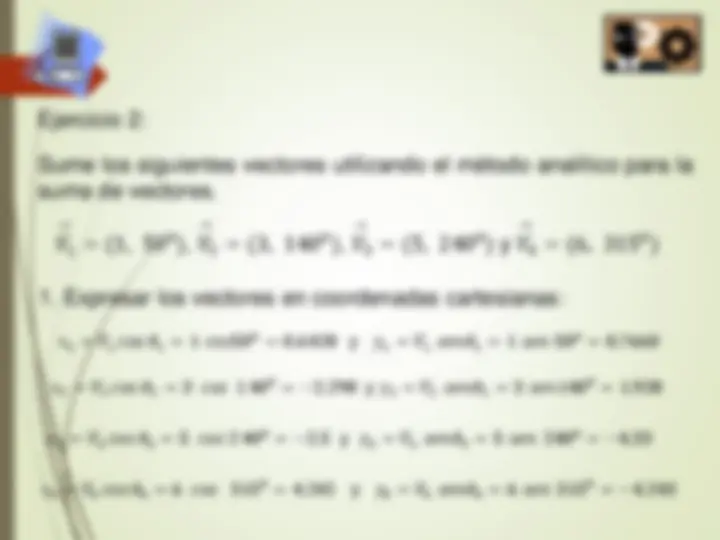
Ejercicio 2 : Sume los siguientes vectores utilizando el método analítico para la suma de vectores. 𝑉 → 1 =^ (^1 ,^50 0 ), 𝑉 → 2 =^ (^3 ,^140 0 ), 𝑉 → 3 =^ (^5 ,^240 0 ) y 𝑉 → 4 =^ (^6 ,^315 0 )

1. Expresar los vectores en coordenadas cartesianas: 𝑥 1 = 𝑉 1 𝑐𝑜𝑠 𝜃 1 = 1 𝑐𝑜𝑠 50 0 = 0. 6428 y 𝑦 1 = 𝑉 1 𝑠𝑒𝑛𝜃 1 = 1 𝑠𝑒𝑛 50 0 = 0. 7660 𝑥 2 = 𝑉 2 𝑐𝑜𝑠 𝜃 2 = 3 𝑐𝑜𝑠 1 40 0 = − 2. 298 y 𝑦 2 = 𝑉 2 𝑠𝑒𝑛𝜃 2 = 3 𝑠𝑒𝑛 140 0 = 1. 928 𝑥 3 = 𝑉 3 𝑐𝑜𝑠 𝜃 3 = 5 𝑐𝑜𝑠 2 40 0 = − 2. 5 y 𝑦 3 = 𝑉 3 𝑠𝑒𝑛𝜃 3 = 5 𝑠𝑒𝑛 240 0 = − 4. 33 𝑥 4 = 𝑉 4 𝑐𝑜𝑠 𝜃 4 = 6 𝑐𝑜𝑠 315 0 = 4. 242 y 𝑦 4 = 𝑉 4 𝑠𝑒𝑛𝜃 4 = 6 𝑠𝑒𝑛 315 0 = − 4. 243

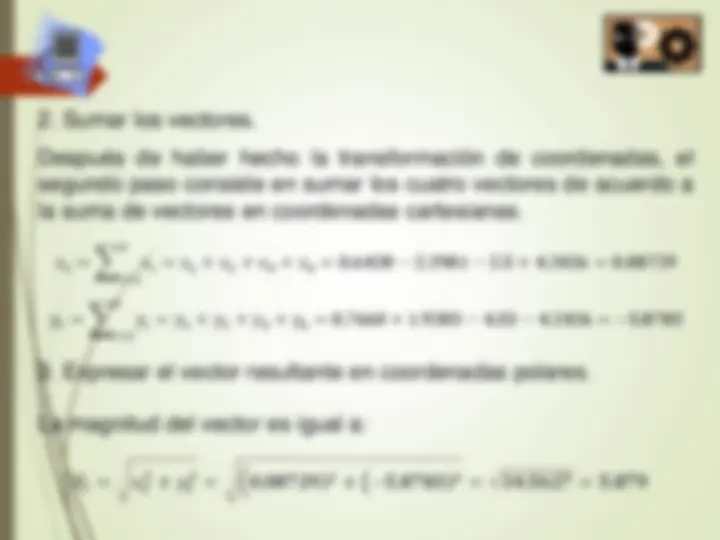
2. Sumar los vectores. Después de haber hecho la transformación de coordenadas, el segundo paso consiste en sumar los cuatro vectores de acuerdo a la suma de vectores en coordenadas cartesianas. 𝑥𝑡 = ෍ 𝑖= 1 𝑛 𝑥𝑖 = 𝑥 1 + 𝑥 2 + 𝑥 3 + 𝑥 4 = 0. 6428 − 2. 2981 − 2. 5 + 4. 2426 = 0. 08729 𝑦𝑡 = ෍ 𝑖= 1 𝑛 𝑦𝑖 = 𝑦 1 + 𝑦 2 + 𝑦 3 + 𝑦 4 = 0. 7660 + 1. 9283 − 4. 33 − 4. 2426 = − 5. 8783
3. Expresar el vector resultante en coordenadas polares. La magnitud del vector es igual a: 𝑉𝑡 = 𝑥𝑡 2

• 𝑦𝑡 2 = ቀ 0. 08729 ) 2
• ൫ − 5. 8783 ) 2 = 34. 5627 = 5. 879

Atentamente: Dr. Guillermo Becerra Córdova Página: http://virtual.chapingo.mx/fis