













Study with the several resources on Docsity

Earn points by helping other students or get them with a premium plan


Prepare for your exams
Study with the several resources on Docsity

Earn points to download
Earn points by helping other students or get them with a premium plan
Community
Ask the community for help and clear up your study doubts
Discover the best universities in your country according to Docsity users
Free resources
Download our free guides on studying techniques, anxiety management strategies, and thesis advice from Docsity tutors
A detailed explanation of stress transformation, a fundamental concept in mechanics of materials. It covers the derivation of formulas for calculating normal and shear stresses at any angle, along with illustrative examples. Particularly useful for students studying mechanics of materials or related engineering disciplines.
Typology: Exercises
1 / 23

This page cannot be seen from the preview
Don't miss anything!
















1
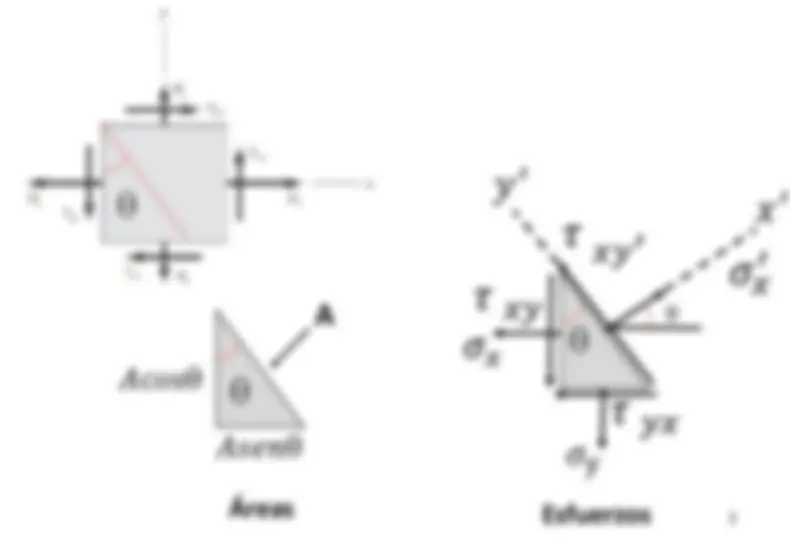
𝜎 𝜎
𝜎𝑥
A 𝜏 𝑥𝑦
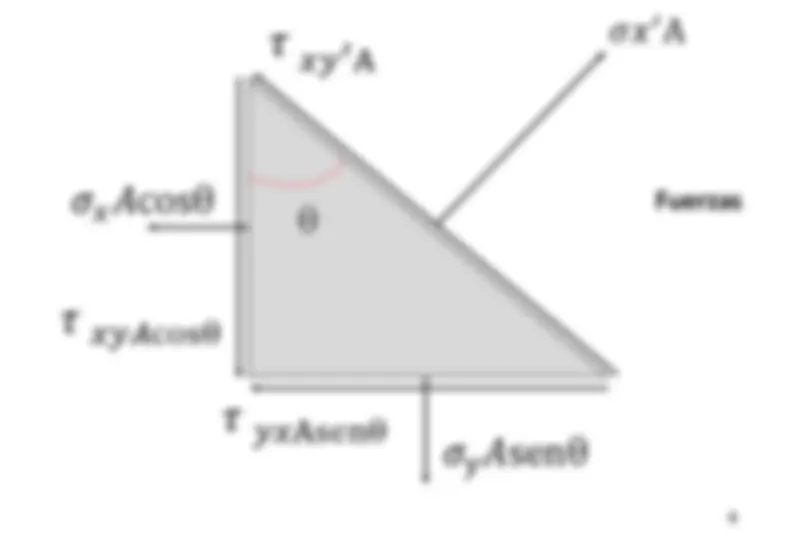
A 𝜏 𝑥𝑦𝐴cosθ 𝜏 𝑦𝑥Asenθ Fuerzas
𝑥 ′ 𝑦 ′
𝜎𝑥
A 𝜏 𝑥𝑦
A
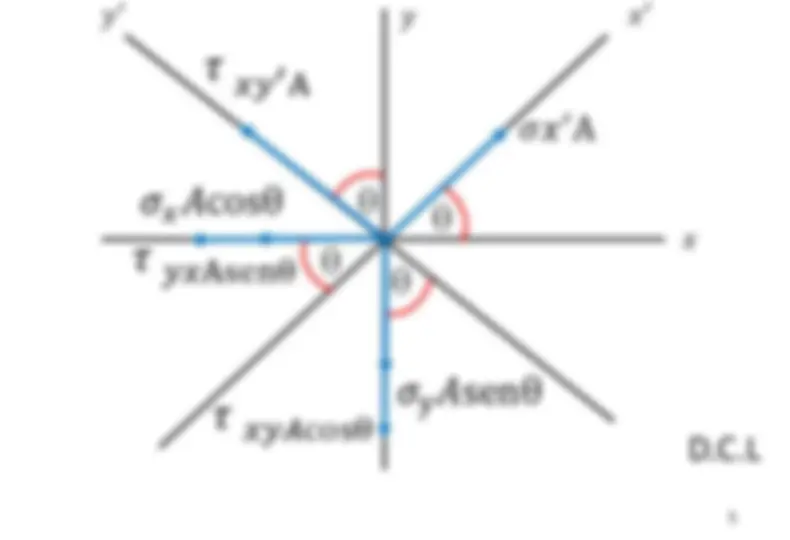
𝜏 𝑦𝑥Asenθ 𝜏 𝑥𝑦𝐴cosθ D.C.L 𝑦 𝑥
′ = 𝜎𝑥cos 2 θ + 𝜎ysen 2 θ + 2 𝜏𝑦𝑥senθcosθ Igualdades Trigonométricas cos
θ = 1 + cos 2 θ
sen
θ = 1 − cos 2 θ
sen 2 θ = 2 senθcosθ
′ = 𝜎𝑥cos 2 θ + 𝜎ysen 2 θ + 2 𝜏𝑦𝑥senθcosθ
𝜎𝑥 ′ = 𝜎 𝑥 ( 1 + cos 2 θ 2 ) + 𝜎 y ( 1 − cos 2 θ 2 ) + 𝜏 𝑦𝑥 sen 2 θ 𝜎𝑥 ′ = ( 𝜎𝑥 2 ) + ( 𝜎𝑥cos 2 θ 2 ) + ( 𝜎y 2 ) − ( 𝜎ycos 2 θ 2 ) + 𝜏 𝑦𝑥 sen 2 θ
y
y
Evaluar esfuerzo normal a cualquier ángulo (Fórmula)
𝛴𝐹𝑦 ′ = 0 0 = 𝜏 𝑥𝑦 ′ A + 𝜎𝑥𝐴cosθsenθ − 𝜎y𝐴senθcosθ + 𝜏𝑦𝑥Asenθsenθ − 𝜏𝑥𝑦Acosθcosθ 𝜏 𝑥𝑦 ′ A = −𝜎𝑥𝐴cosθsenθ + 𝜎y𝐴senθcosθ − 𝜏𝑦𝑥Asenθsenθ + 𝜏𝑥𝑦Acosθcosθ 𝜏 𝑥𝑦 ′ A = (𝐴) − 𝜎𝑥cosθsenθ + 𝜎ysenθcosθ − 𝜏𝑦𝑥senθsenθ + 𝜏𝑥𝑦cosθcosθ 𝜏 𝑥𝑦 ′ = −𝜎𝑥cosθsenθ + 𝜎ysenθcosθ − 𝜏𝑦𝑥senθsenθ + 𝜏𝑥𝑦cosθcosθ 𝜏 𝑥𝑦
𝑥cosθsenθ^ +^ 𝜎ysenθcosθ^ −^ 𝜏𝑦𝑥sen 2 θ + 𝜏𝑥𝑦cos 2 θ
𝑥𝑦 ′ = −𝜎𝑥cosθsenθ + 𝜎ysenθcosθ − 𝜏𝑦𝑥sen 2 θ + 𝜏𝑥𝑦cos 2 θ Igualdades Trigonométricas cos
θ = 1 + cos 2 θ
sen
θ = 1 − cos 2 θ
sen 2 θ = 2 senθcosθ
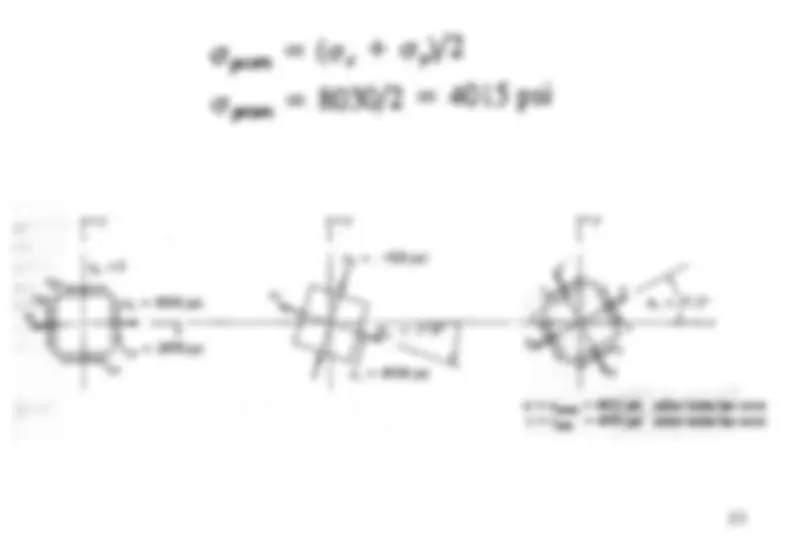
Esfuerzos Principales (Fórmulas Importantes)
Esfuerzos Principales (Ejemplos Sencillos)