Download Solution of Exam 2 - Algorithms - 2009 | CSCD 320 and more Exams Algorithms and Programming in PDF only on Docsity!
CScD-320, Algorithms
Exam 2: 12 May 2009
Exam Key
1. (5 points) For the following general tree, list
the order in which nodes will be visited in the
following two different traversals.
(a) Pre-order
A B E F C G D H J
(b) Post-order
E F B G C H J D A
2. (5 points) Draw the associated binary tree for the tree in the previous question.
A B E (^) F G H J C D A B C D E F G H J
3. (5 points) If unique keys are required, what is the relationship between every node in a Binary
Search tree with its left child (if one exists) and with its right child (if one exists)? Left child compares as less than the node, and the node compares as less than the right child.
4. (5 points) What is the AVL condition? That is, what is true at every node of a valid AVL tree
that makes it an AVL tree rather than just a Binary Search Tree (BST)? At each AVL node, the heights of the two child nodes differ from each other by at most one. Printed 2020/ 12 月/4 at 12:54 Page 1 A B E (^) F G H J C D
Spring 2009: Exam 2
For the next two questions, assume the following class attributes ( no attribute for size):
public class BSTnode { Comparable key; // Basis for ordering BSTnode left, // Reference to the left subtree right; // Reference to the right subtree.
5. (5 points) Write the recursive Java method to determine the number of nodes of a binary
tree rooted at the node passed as the parameter. Hint: size(null) is zero.
int size (BSTnode t) { // and the rest is up to you!
return t == null? 0 : 1 + size(t.left) + size(t.right);
6. (10 points) Write the method to list the keys — that is, the contents of node.key — in
nonascending order (that is, largest to smallest) to System.out, one per line. You are given the public method that calls the recursive method you are writing. public void reverseList() { if (root == null) System.out.println("Empty list"); else reverseList(root); } void reverseList ( BSTnode node ) { //and the rest is up to you
while node != null ) // Removing tail recursion
{ reverseList(node.right);
System.out.println (node.key);
node = node.left
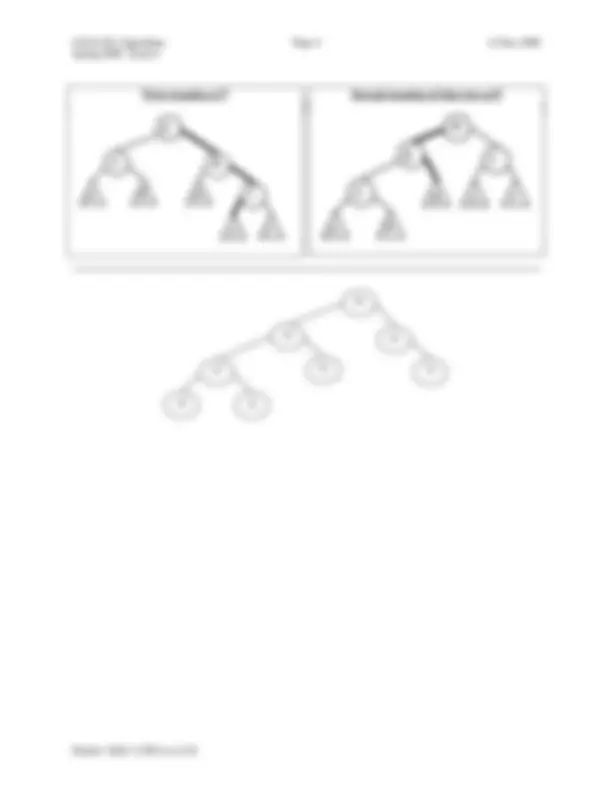
Spring 2009: Exam 2 First rotation at T
C R
a g^ T
s v
E
d
Second rotation of that tree at E R C a g T s v E d 20 25 40 49 50 58 63 70
Spring 2009: Exam 2
10. (5 points) Beginning with the above (valid) AVL tree, show (a) the tree resulting from inserting 30 , and then (b) the AVL tree, after corrections, if any are needed ,. If no corrections are needed, show expressly by the heights of the nodes why none are needed. Type 2 (LR) 20 25 40 49 50 58 63 70 30 20 25 40 49 50 58 63 70 30
11. (5 points) Beginning with the AVL tree at the top of the [previous] page ( not the result of the last
question), show (a) the tree resulting from deleting 63 , and then (b) the AVL tree, after corrections, if any are needed. If no corrections are needed, show expressly by the heights of the nodes why none are needed.
12. (5 points) What must be true about an m -way tree for it to be a valid B-tree? You may presume that m is
odd for your answer. All nodes other than the root have at least m/2 -1 values ( m/2 children if non-leaf). The root has at least one value (and two children if a non-leaf node). All leaf nodes are at the same level. Type 1 (LL) 20 25 40 49 50 58 70 20 25 40 49 58 50 70
