



























































Study with the several resources on Docsity

Earn points by helping other students or get them with a premium plan


Prepare for your exams
Study with the several resources on Docsity

Earn points to download
Earn points by helping other students or get them with a premium plan
Community
Ask the community for help and clear up your study doubts
Discover the best universities in your country according to Docsity users
Free resources
Download our free guides on studying techniques, anxiety management strategies, and thesis advice from Docsity tutors
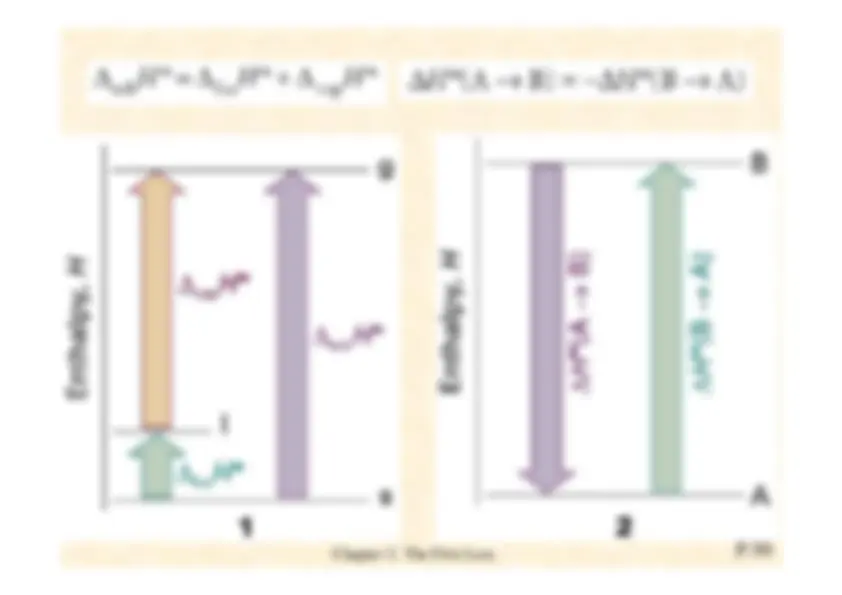
Enthalpy is the sum of the internal energy and the product of pressure and volume and its general formula is H=U+PV.
Typology: Slides
1 / 71

This page cannot be seen from the preview
Don't miss anything!
































































Chapter 2. The First Law.
P.
Justification 2.
The relation
∆
H = q
p
-^
For a general infinitesimal change in the state of the system,
U
changes to
U +
d U
,^ p
changes to
p +
d
p , and
V
changes to
V +
d
V , so
H
changes from
U + pV
to
Recognize
U
pV
=
H
on the right,
H
changes to
Now substitute d
U
= d
q^
w^
into this expression,
If the system is in mechanical equilibrium with its surroundings at a pressure
p
and does only expansion work, we can write d
w^
= −
p d
V^
and obtain
Now impose the condition that the heating occurs at constant pressure bywriting d
p^
= 0. Then
-^
dH=dq (at constant p, no additional work)
Example 2.
Relating
∆
H and
∆
U
-^
The internal energy change when 1.0 mol CaCO
in the form of calcite 3
converts to aragonite is +0.21 kJ. Calculate the difference between theenthalpy change and the change in internal energy when the pressure is 1.0bar given that the densities of the solids are 2.71 g cm
−
and 2.93 g cm
−3,
respectively.
-^
Answer:
-^
The volume of 1.0 mol CaCO
(100 g) as aragonite is 34 cm 3
3 , and that of 1.
mol CaCO
as calcite is 37 cm 3
(1 Pa m
3 = 1 J). Hence,
only 0.1% of
∆
U
. Usually ignore the difference between H and U of
condensed phases, except at very high p, when
pV
no longer negligible
-^
Self Test 2.
Calculate the difference between
∆
H
and
∆
U
when 1.0 mol Sn(s,
grey) of density 5.75 g cm
−
changes to Sn(s, white) of density 7.31 g cm
−
at
10.0 bar. At 298 K,
∆
H = +
2.1 kJ.
-^
Correct Answer:
∆
H −
∆
U = −
4.4 J
Enthalpy of perfect gas
Illustration 2.
The relation between
and
U for gas-phase reactions
(g) + O 2
(g) 2
O(l), 2
n
g^
3 mol. At 298 K, when
= 2.5 kJ
mol
−
, the enthalpy and internal energy
changes in the system
g)/(18.02 g mol
−
) = (0.798/18.02) mol H
the enthalpy of vaporization per mole ofH
O is 2
O(l) 2
O(g) , 2
n
g^
= +1 mol,
benzene at its boiling point (353.25 K) is30.8 kJ mol
−
. What is the molar internal
energy change? For how long would thesame 12 V source need to supply a 0.50 Acurrent in order to vaporize a 10 g sample?
-^
Correct Answer:
+27.9 kJ mol
−
, 660 s
Chapter 2. The First Law.
P.
2.5(c) The variation of enthalpy with temperature
Example 2.
Evaluating an increase in enthalpy with temperature
(p.45)
2
when it is heated from 25
°C to 100
( Table 2-2)
Chapter 2. The First Law.
P.
2.6 Adiabatic changes
Adiabatic processes
-^
Consider a stage in a reversible adiabaticexpansion when the pressure inside and out is
p
.
The work done when the gas expands by d
V
is
d
w
= −
p
d
V
; however, for a
perfect gas
, d
U
=
C
dV
T
.
-^
Therefore,because for an
adiabatic
change (d
q
= 0)
d
U
= d
w
q
= d
w
, we can equate these two
expressions for d
U
and write
We are dealing with a
perfect gas
, so we can
replace
p
by
nRT
/ V
and obtain
x
/ y
) = −ln(
y
/ x
), this expression
rearranges to
c
nR
we obtain (because ln
x
a^
a
ln
x
/f
)i c^
/i
) and,f
upon rearrangement,
Adiabatic processes
(4)
-^
The initial and final states of a perfect gas satisfy theperfect gas law regardless of how the change of statetakes place, so use
pV
=
nRT,
However, we have just shown that
where we use the definition of the heat capacity ratiowhere
γ
=
C
p ,m
/ C
V ,m
and the fact that, for a perfect
gas,
C
p ,m
C
V ,m
=
R
(
Sec.2.
). Then we combine the
two expressions, to obtain
which rearranges to
p
V i
γi
=
p
V f
γf
Illustration 2.
Work of adiabatic expansion
-^
Consider the adiabatic, reversible expansion of 0.020mol Ar, initially at 25
°C, from 0.50 dm
3
to 1.00 dm
The molar heat capacity of argon at constant volume is12.48 J K
−
mol
−
, so
c
= 1.501. From
It follows that
∆
T = −
110 K, from
Note that temperature change is independent of theamount of gas but the work is not.
-^
Test 2.
Calculate the final temperature, the work done,
and the change of internal energy when ammonia isused in a reversible adiabatic expansion from 0.50 dm
3
to 2.00 dm
3 , the other initial conditions being the same.
-^
Correct Answer:
195 K, −56 J, −56 J
Illustration 2.
The pressure change
accompanying adiabatic expansion
at 100 kPa expands reversibly andadiabatically to twice its initial volume thefinal pressure will be
final pressure would be 50 kPa.