






















































Study with the several resources on Docsity

Earn points by helping other students or get them with a premium plan


Prepare for your exams
Study with the several resources on Docsity

Earn points to download
Earn points by helping other students or get them with a premium plan
Community
Ask the community for help and clear up your study doubts
Discover the best universities in your country according to Docsity users
Free resources
Download our free guides on studying techniques, anxiety management strategies, and thesis advice from Docsity tutors
Solutions to practice exam distributed on Thursday (Do not distribute!) ... Security Definition(s): Authenticated Encryption, CCA-Security, CPA-Security.
Typology: Exercises
1 / 65

This page cannot be seen from the preview
Don't miss anything!


























































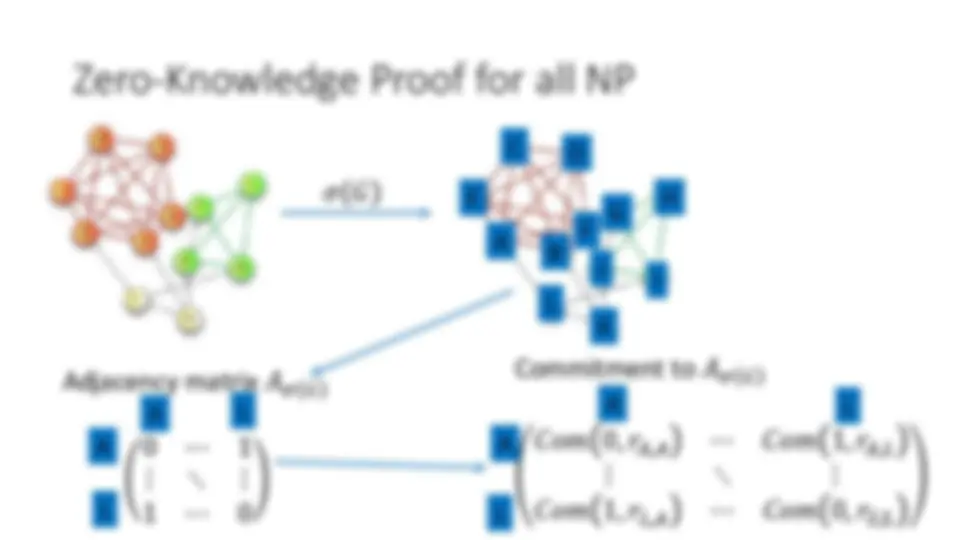
Protocol: