













Study with the several resources on Docsity

Earn points by helping other students or get them with a premium plan


Prepare for your exams
Study with the several resources on Docsity

Earn points to download
Earn points by helping other students or get them with a premium plan
Community
Ask the community for help and clear up your study doubts
Discover the best universities in your country according to Docsity users
Free resources
Download our free guides on studying techniques, anxiety management strategies, and thesis advice from Docsity tutors
This document, from a phys 375 - spring 2008 lecture by p. Piot, covers the topics of signal transmission through transmission lines, coupling schemes, and noise. The need to propagate signals over long distances, the use of transmission lines and coupling schemes, and the modeling of transmission lines using the wave equation. The document also covers the effects of noise, including white noise, pink noise, and thermal noise, and methods for dealing with noise such as impedance matching and the use of lock-in amplifiers.
Typology: Lab Reports
1 / 20

This page cannot be seen from the preview
Don't miss anything!













P. Piot, PHYS 375 – Spring 2008
Signal Transmission^ – Coupling scheme– Transmission line– Termination & impedance matching
-^
Noise^ – White noise– Pink noise– Lock-in amplifier: measuring modulated signal buried into
noise
P. Piot, PHYS 375 – Spring 2008
-^
There is often a need to propagate a signal over long distance
-^
This is accomplished with a transmission line in electronics
-^
Fancier system convert electronic signal into an optical pulses anduse fiber to propagate signal over very long distance (e.g.communication cable under Atlantic ocean)
-^
The fundamental questions are:– How do we “inject” a signal into a transmission line– How do we model the effect of long transmission line on the
electrical signal
on the signal and avoid reflections and/or interferences
P. Piot, PHYS 375 – Spring 2008
-^
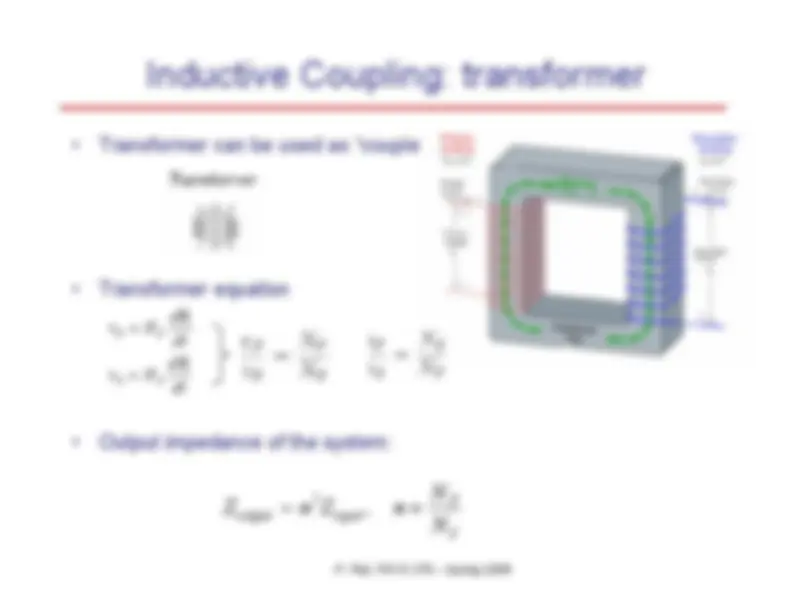
Transformer can be used as “couplers”
-^
Transformer equation
-^
Output impedance of the system:
d^ dt N v
d dt N v
S S
P P
Φ
=
Φ
=
P S
input
output
2
P. Piot, PHYS 375 – Spring 2008
-^
You already used this cable in the Lab (to connectoscilloscope or frequency generator to you circuits)
-^
How do we model this cable?
P. Piot, PHYS 375 – Spring 2008
-^
Introduce the capacitance dC=c
dx 0
and inductance
dL=l
dx 0
per unit of length.
-^
We can apply Kirchoff’s voltageand current low to on LC cell ofthe circuit
2 2 0 0
2 2
dV dt c
dI dx
0 − =
0
0
0
P. Piot, PHYS 375 – Spring 2008
-^
So the wave equation is satisfied by both
I^
and
V
-^
This are wave equations (in electromagnetism bothscalar and vector potentials associated to an e.m.wave obey this equation)
-^
The
l^0
c^0
quantity has the dimension [L
-2^ .T
2 ]:
-^
The solution of the wave equation are of the form:
]
[
) , (
) , (
) ( 1 ) ( 0 ) ( 1 ) ( 0
kx t i
kx t i
kx t i
kx t i
e I e I Z t x V e I e I t x I
−
−
−
=
=
ω
ω
ω
ω
0
0
2 2 0 0
2 2
=
−
V^ I
d dt c l
V I
d dx
P. Piot, PHYS 375 – Spring 2008
-^
Suppose at
x=L
we connect a resistor with resistance R then, at
x=L we have
-^
So the current and voltage take the formwith
r^
being a reflection coefficient
-^
r=
if Z=R (impedance matching)
-^
ikL
kLt i
kLt i
kLt i
kLt i
e I Z R
Z R I
e I
e I R
eI
e I Z
t L x RI t L x V
2 0
1
) ( 1 ) ( 0 ) ( 1 ) ( 0 ]
[
]
[
) , ( ) , (
−
−
− − + =
⇒
=
−
⇒
=
=
=
ω
ω
ω
ω
] ≡
[
) , (
]
[
) , (
) (
) ( 0
) (
) ( 0
kxt i
kxt i
kxt i
kxt i
re
e ZI t x V
re
e I t x I
−
−
=
−
=
ω
ω
ω
ω
P. Piot, PHYS 375 – Spring 2008
-^
If^
termination is open
(R
)^ then
r=exp (-i2kL)
and the voltage
becomes this is a stationary wave!
-^
If^
termination is closed
(short circuit: R=0)
then
r=-exp (-i2kL)
and
)
(
cos )
cos(
2
) , (^
0
L
x k
kL t
V
t x V
−
−
=
ω
)
(
sin )
sin(
2
) , (^
0
L
x k
kL t
V
t x V
−
−
ω
P. Piot, PHYS 375 – Spring 2008
-^
Combination of a forward andbackward traveling wave yieldsa standing wave: SIGNAL DOES NOT PROPAGATE
P. Piot, PHYS 375 – Spring 2008
-^
In a conductor electron have random motion due to temperature.
-^
The
power spectral density
(=mean square voltage per unit of
frequency in
V
2 /Hz
) associated to this thermal noise is:
-^
So the rms voltage noise is
-^
and the rms current noise is Noise: Thermal Noise (or Johnson–Nyquist noise )
kTR
e hf kT kTR
V df d
hf^ kT
4 1 1
4 2
≈ −
=
R
f kT
I^
∆
=^
2 (^2) / 1 2
R: resistance,k: Boltzmann const.h: Planck const.T: temperature [K]f: frequency [Hz] Frequency bandwidth
f kTR
V^
∆
=^
2 (^2) / 1 2
“Low” frequency (f<1 GHz) approximation
P. Piot, PHYS 375 – Spring 2008
-^
Shot and Thermal noise are white noise (no frequency dependenceon power)
-^
Colored noise also exit typically
-^
When
α
=1 noise is refered to as
“ pink
” noise or
1/f
noise
-^
In electronics pink noise is dueto a variety of cause: impurity,carrier/hole recombination, …
-^
Flicker noise appear for instancein resistors and transistors
α f
V df d^
1
2
∝
P. Piot, PHYS 375 – Spring 2008
-^
Work with small bandwidth system, optimize the bandwidth for thesignal
-^
Can use RC filter to cut both hand of the spectrum
-^
A figure-of-merit to quantify noisecompared to the main signal is the S/N ratio
-^
Most of the time engineers like to express this S/N ratio asthe unit of S/N is this latter expression is
Decibel
(Symbol Db)
-^
Some practical “conversion”:
How do we deal with and characterize noise?
(^
)
(^
)
(^
)^
Db
Db Db
PsignalPnoise N S^
≡ /
(^
)^
Db
10
P. Piot, PHYS 375 – Spring 2008
Detection of ultra-low signal buried in noise:
The lock-in amplifier
)
cos(
)
cos(
ϕ
ω ω
=
=
t
B
B
N
t
A
A
)
cos( ˆ
)]
cos( )
2
[cos( ˆˆ^2
)
cos( ˆ )
cos()
cos( ˆ ˆ
ϕ
ω
ϕ
ϕ
ω
ϕ
ω
ϕ
ω
ω
=
=
t N A t B A
t N A t t B A
AB
P. Piot, PHYS 375 – Spring 2008
Lock-in amplifier: a numerical example