











Study with the several resources on Docsity

Earn points by helping other students or get them with a premium plan


Prepare for your exams
Study with the several resources on Docsity

Earn points to download
Earn points by helping other students or get them with a premium plan
Community
Ask the community for help and clear up your study doubts
Discover the best universities in your country according to Docsity users
Free resources
Download our free guides on studying techniques, anxiety management strategies, and thesis advice from Docsity tutors
Algorithms and examples for converting numbers from one base to another, including base 10, base 16, and base c. It also covers converting base b fractions to base c and vice versa. Additionally, it discusses different number representations such as sign-magnitude, radix complement, and diminished radix complement.
Typology: Slides
1 / 23

This page cannot be seen from the preview
Don't miss anything!
















1
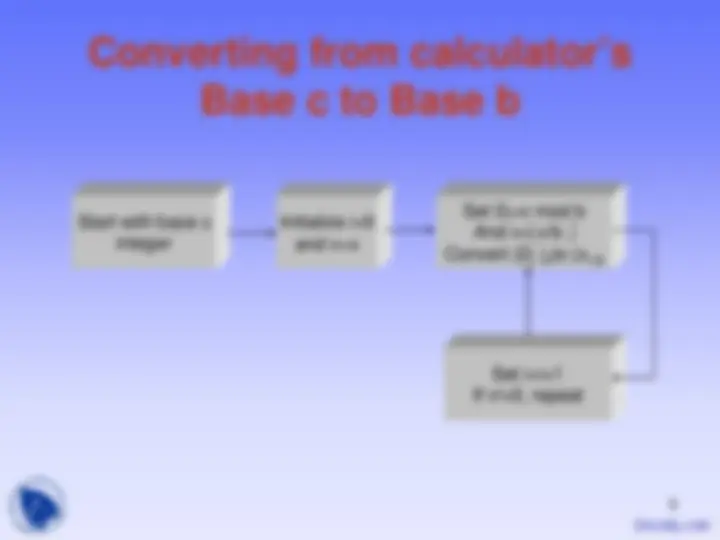
Start with base b representation
Initialize base c value x to 0
Get next xi Going from left to right
Convert (xi) (^) b number (D (^) i) (^) c by using table
Update the base c value by x=xb+D (^) i
Initialize base c value x to 0
Repeat for All digits
x (^) m-1…x1x (^0)
2
Example: Convert the Hexadecimal
number B3 16 to base
10
Solution:
According to the above algorithm,
X=
X=x+B(=11)=
X=16*11+3= 179
Hence B3 16 =179 (^10)
4
Example: convert 390 10 to base 16
c=10, b=
Solution:
5
Converting a Base b fraction to calculator’s Base c
Start with base b representation
Initialize f=0.0 and Set i = -m
Convert to Base c number (Di) (^) c by using table
Update f=(f+D)/b And i=i+
Repeat for all digits until i= Here the digits are treated from right to left, with division implemented at each step
f (^) -1 f (^) -2 …f (^) -m x (^) n-1x (^) n-2…x 1 x 0 .x-1 x (^) -2 …x-m
7
Converting a fraction from calculator’s Base c to Base b
Start with fraction f in Base c Initialize i=1 and v=f
Set D (^) -i=bv and v=bv - D (^) i Convert D (^) i to f-i
Set i=i+ If v!=0 repeat Until enough digits are generated
No division is required and the process should be terminated when enough digits are generated
8
Example: Convert 0.24 10 to base 2
Solution:
0.24*2=0.48, f-1=
0.48*2=0.96, f-2=
0.96*2=1.92, f-3=
0.92*2=1.84, f-4=
0.84*2=1.68, f-5=1,…
Thus 0.24 10 =(0.00111) 2
10
11
13
Example Base 2 Complement representation
Number Representation Number Representation
0 0 0 0 or 255
0<x<128 x 0<x<128 x
-128<=x<0 256-|x| -127<=x<0 255 -|x|
8 bit 2’s complement 8 bit 1’s complement
14
Examples of number representations
Decimal 2’s complement
1’s complement
Sign- magnitude
16’s complement
Unsigned
27 011011 011011 011011 1B 11011
.17 0.00101011^ 0.00101011^ 0.00101011^ 0.2B 0.
-26 100110 100101 111010 E6 -
-0.57 1.01101110 1.01101101 1. 10
F.6E -
16
Example: Multiplication and division of negative numbers
-6=(11010) (^2) -6x4=(01000) 2 =8 which is wrong! using less no. of bits might change sign
So, -6=(111010) (^2)
-6x4=(101000) 2 = -
17
Example: Multiplication and division of negative numbers
-24=(101000) (^2) -24x2=(010100) 2 = -24x2=(110100) 2 = -
Changing the size of the number,
24=011000 (n=6) to 00011000 (n=8) -24=101000 (n=6) to 11101000 (n=8)
19
Base 16 addition Base 2 addition
A B 4 2 16
20
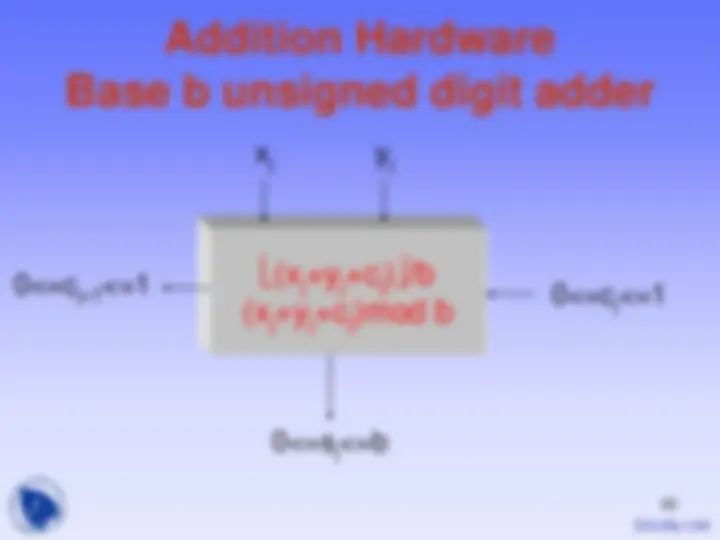
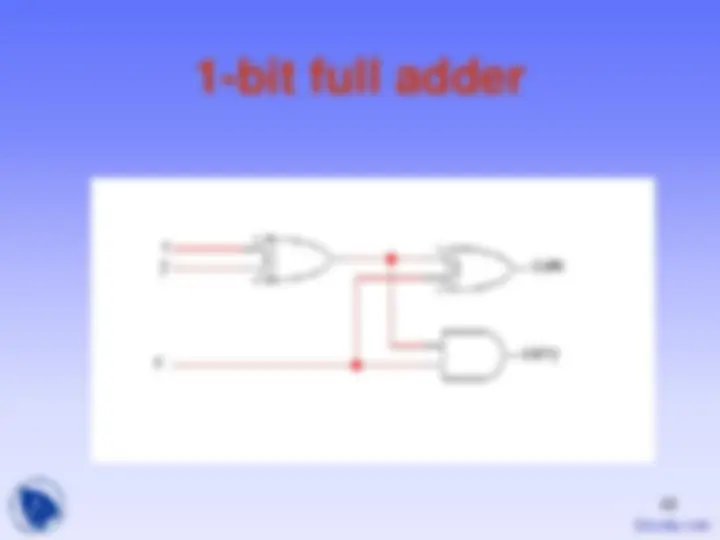
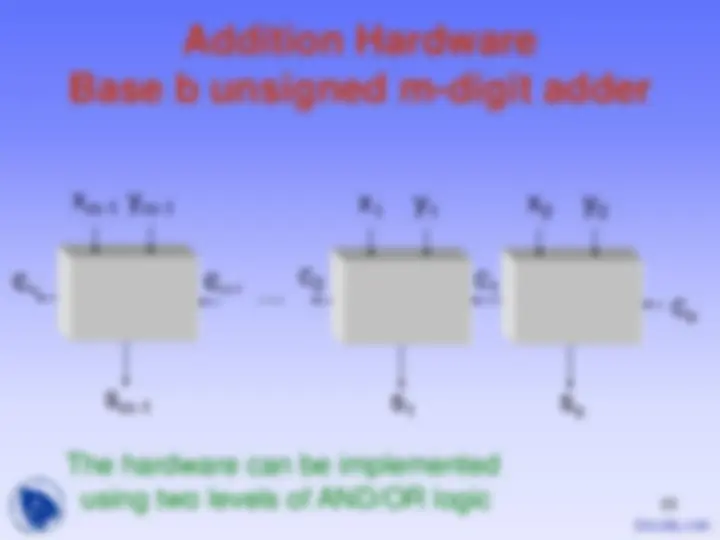
Addition Hardware Base b unsigned digit adder
(x (^) j+y (^) j+c (^) j)/b (x (^) j+y (^) j+c (^) j)mod b
x (^) j y (^) j
0<=cj+1 <=
0<=s (^) j<=b
0<=cj<=