Download Radiation - Lecture Notes - Relativity Part I | Phys 315 and more Study notes Physics in PDF only on Docsity!
Chapter-1 Relativity Part I
RADIATION
- Radiation implies the transfer of energy from one place to another.
- Electromagnetic Radiation - Light
- Particle and Cosmic Radiation – photons, protons, neutrons, electrons pions, etc.
- Solar Radiation – ionized electrons- plasma
- Thermal Radiation - Infrared
- Ultraviolet Radiation -
- Ultrasonic Radiation - Ultrasound >50KHz
- Maxwell showed that the electromagnetic radiation (EM) can be explained by a plane wave
- Energy transfer is given by the Poynting Vector S = 1/ μ o E x B (W/m^2 ) W/m^2 (Energy/time)/area
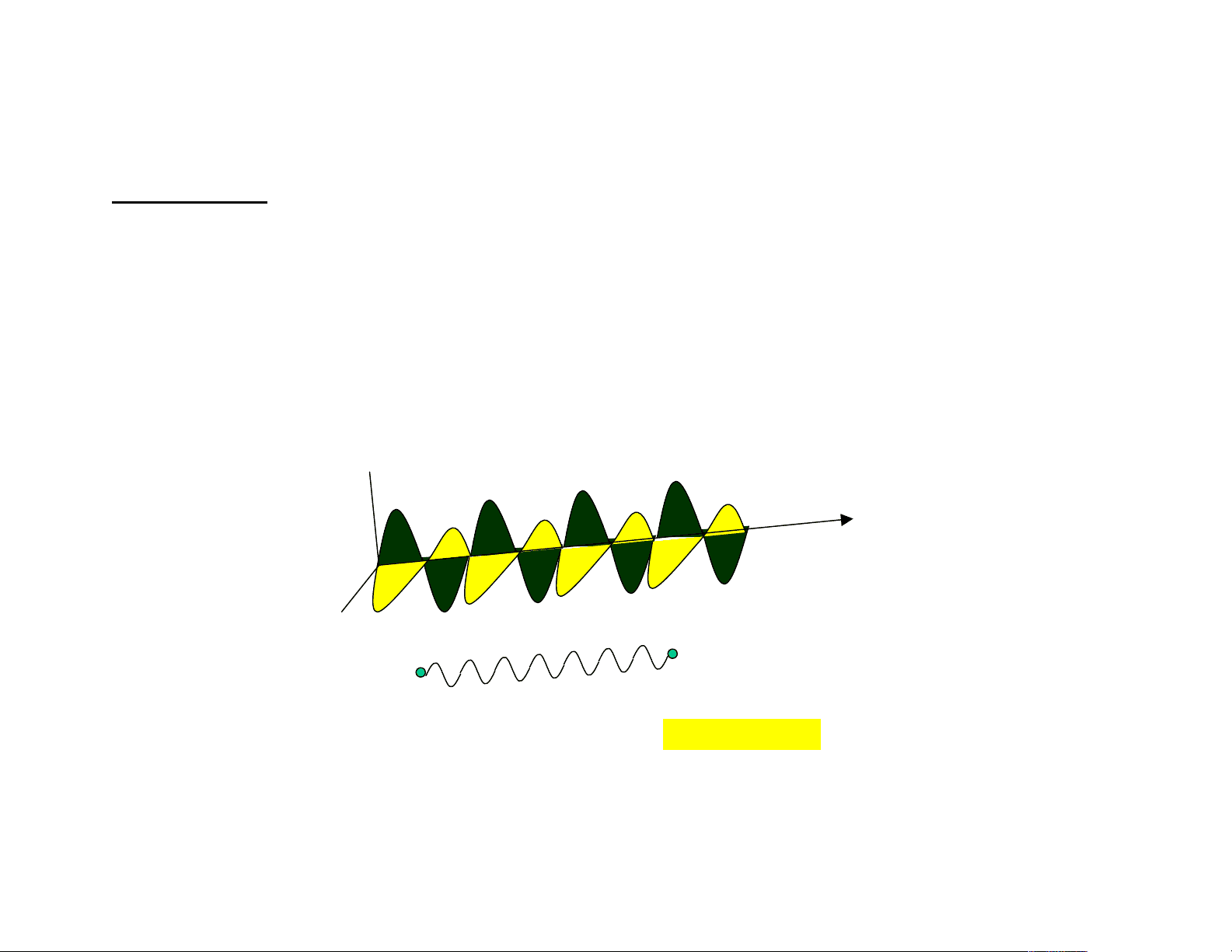
E
B
Plane Wave
v = c
a
b
DIPOLE ANTENNA
Consider a dipole antenna emitting EM radiation. The E-field follows the charge up and down, The B-field circulates about the current I flow up and down.
JOULE HEATING
E = ( V/d ) k d = length of the antenna B = ( μo I/ 2πR ) i R = radius of the antenna wire
S = ( V /d) ( μo I/ 2πR ) k x i = ( V /d) ( μo I / 2πR ) j
Power emitted from the surface of the antenna P = S x Area P = 1/ μo {(V/d) ( μo I/ 2πR )} 2πR d = I V P =IV (Watts) V = IR (Ohm’s Law)
R
d
E
B
V - Oscillator i
j
I k
- In 1856 Maxwell's equations represent one of the most elegant and concise ways to state the
fundamentals of electricity and magnetism. He assumes the speed of light c to be constant.
- In 1888 Heinrich Hertz measured the speed of electromagnetic waves produced in his laboratory to be about 300,000 km/s strongly implying the light and electromagnetic waves are the same thing!
- Top scientist believe we are traveling through an ether and the speed of light must be affected! This is inconsistent with Maxwell’s theory.
- “The Laws of motions were the same throughout the universe” , why not the laws of Electromagnetism??
- Does light needed a medium to travel in ?? Don’t all waves need a medium to travel ??
Hertz Dipole Antenna Waves
E
ETHER HYPOTHESIS
- Our relative motion to the ether must be considered.
- Earth moves through a stationary Ether?
- Stars are fixed in place relative to this motion.
- Copernicon View.
- Aberration of Starlight- Telescope tilt dependent on velocity through the either!
- ABERRATION OBSERVED
- tan θ = VE /c = 9.9 x 10-^5 rdn
V
V=
c
V
θ
- Earth drags the Ether along?
- The earth is a special nonCopernicon frame.
- No Aberration of Starlight - telescope tilt independent of the Earth’s velocity. REJECTED BY EXPERIMENT !!
V
V
7
MICHELSON-MORLEY EXPERIMENT - 1887
- Michelson invents the interferometer.
- Michelson and Morley use the Interferometer to test the ether hypothesis circa 1887.
- No interference pattern was seen. Light took exactly the same Time to travel both paths!
ETHER HYPOTHESIS BUSTED - NO ETHER!!
LORENTZ- FITZGERALD CONTRACTION
- In a “last ditch effort” Lorentz and Fitzerald propose that the apparatus has shrunk L->L/γ due to the ether by just the factor needed to “save the ether”. But not well accepted.
Light source 2nd slit
Mirror- 1
Mirror- 2
Beam Splitter - 0 L
Interference Pattern or not? Not?
V Ether Wind
β = V/c Relative speed 0 1
γ = (1- β^2 )-1/^2 Lorentz factor 1
EINSTEIN’s POSTULATES OF RELATIVITY
- The Principle of Relativity - All physical laws have the same form in all inertial reference (non-accelerating) frames.
- Electricity and Magnetism and Mechanics on the same footing.
- The Consistency of the Speed of Light- The speed of light c in the same in all inertial reference frames. How can this be??
- Einstein proposes a picture of 4-dimensional spacetime- ( x y z t ) in which c = constant!
- Newton’s Laws are shattered.
- Maxwell’s Electromagnetic Theory survives.
V
A
B c
c c +V
RELATIVISTIC DOPPLER SHIFT
Consider light of frequency fo being emitted from a source. An outside Observer will measure a shifted frequency coming from the source
!
f = fo^1 "^ # 1 + #
Source moving away from the Observer with relative speed β. RED SHIFT
!
f = fo^1 +^ " 1 # "
Source moving toward the Observer with relative speed β. BLUE SHIFT
λ = f / c
600nm 500nm 400nm
fo
f <fo (^) f >fo
LORENTZ TRANSFORMATION
Einstein used the Lorentz transformation to form a 4-dimensional spacetime.
Let x’ t’ denote the position and time in the laboratory system Let x t denote the position and time in the moving system.
Lorentz Transform Derivative x’ = γ (x + vt) dx’ = γ (dx + v dt) t’ = γ (t + v x/c^2 ) dt’ = γ (dt + v dx/c^2 )
Velocity Transform Vx’ = dx’/dt’ = (dx + β cdt ) / (cdt + β dx )
v= relative velocity Vx = velocity of an object in the moving frame. Vx’ = velocity of the same object as measured in the Lab frame.
Vx << c Vx’ = Vx + v NEWTON Vx = c (flashlight) Vx’ = c EINSTEIN
Lab
Moving β=v /c
x ct
x’ ct’
!
Vx '= Vx^ +^ v 1 + Vx • v / c^2
Lab
Vx=c
Vx’=?
β=v/c
