Download Problem Set 7: Chiral Dynamics and Quark Masses in QCD and more Assignments Physics in PDF only on Docsity!
Problem Set 7
Due: By classtime, Nov. 12, 2008
- [20 pts] Using the square-root representation of the non-linear σ model, as defined in Ch. IV of Donoghue et al. as (keeping only the most relevant terms)
L =
[
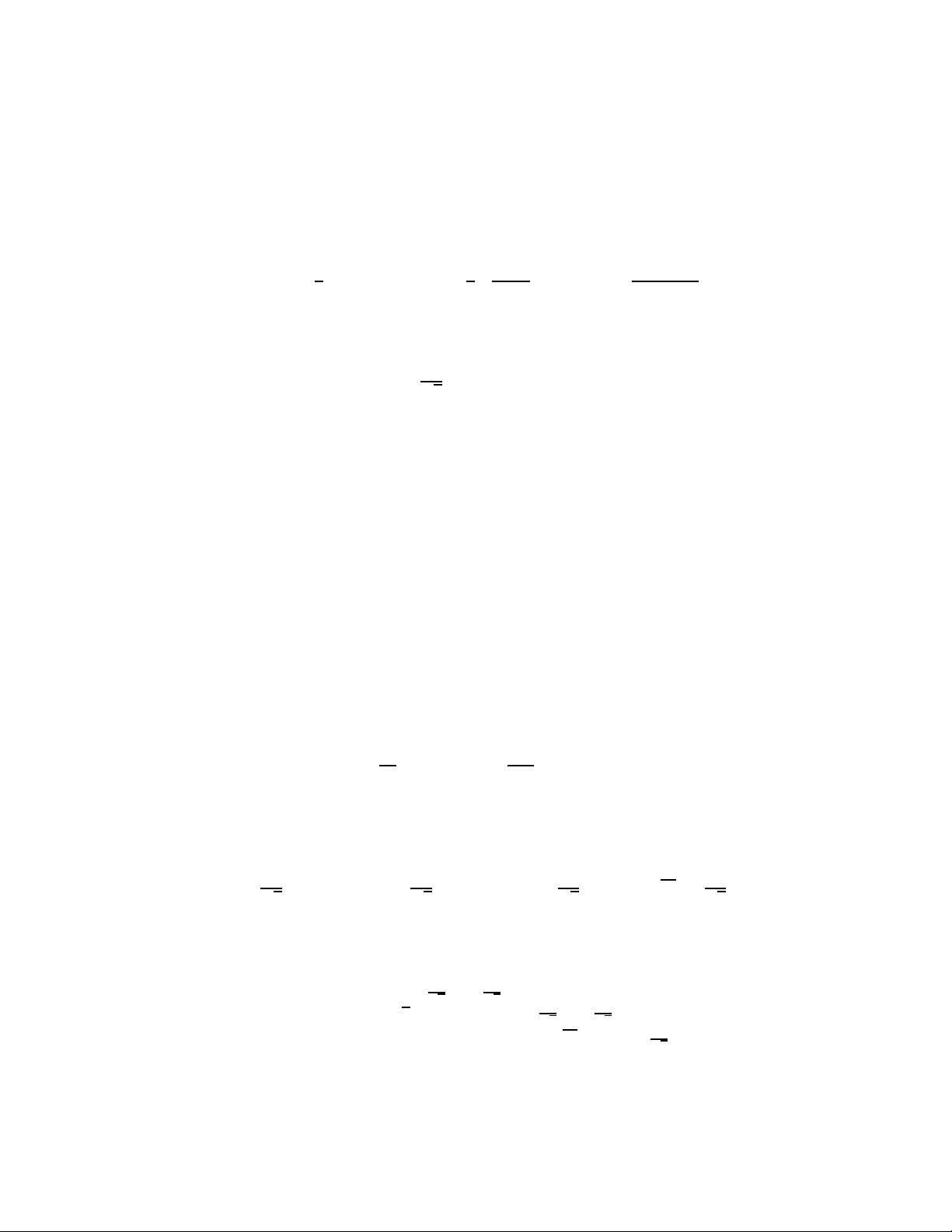
(∂μS)^2 − 2 μ^2 S^2
]
v + S v
) 2 [
(∂μϕi)^2 + (ϕi∂μϕi)^2 v^2 − ϕ^2 i
]
Here S plays the role of either ρ or σ in our other parametrizations, and in the end we would take μ → ∞ to decouple it from the theory. Using again the definitions
π±^ =
(ϕ 1 ∓ iϕ 2 ) , π^0 = ϕ 3
calculate the tree level amplitude for π+π^0 → π+π^0 scattering. The two diagrams are the same as in class, and why doesn’t the the second diagram contribute? You should write down the relevant Feynman rules for the Sϕiϕi and the quartic ϕi interactions (be careful, since these will involve momenta).
- [10 pts] The nice thing about starting from the QCD Lagrangian is that it easily generalizes to nf flavors of light quarks. In other words, if we didn’t assume that just the up and down quarks were light, we could say we had an approximate
SU (nf )L × SU (nf )R
chiral symmetry. Of course, it would be absurd to think we could treat all six quarks as nearly massless, but it is not much of a stretch to set nf = 3 and include the strange quark. Thus, the required symmetry breaking pattern would be
SU (3) × SU (3)R → SU (3)V
This would give rise to 8 Goldstone Bosons, which we can identify as the 8 lightest pseudoscalar mesons: the pions, the kaons, and the η. The corresponding chiral Lagrangian looks exactly the same as the SU (2) case: L = f 2 4
Tr[∂μΣ†∂μΣ] + μf 2 2
Tr[M Σ + Σ†M ]
but now everything here is a 3 × 3 matrix. We have Σ = exp[iφaλa/f ], where λa^ are the Gell-Mann matrices, and we have the quark mass matrix M = diag(mu, md, ms).
(a) Show that with the definitions
π±^ =
(φ^1 ∓ iφ^2 ), K±^ =
(φ^4 ∓ iφ^5 ), K^0 =
(φ^6 − iφ^7 ), K 0 =
(φ^6 + iφ^7 ),
π^0 = φ^3 , η = φ^8 and using the Gell-Mann matrices that
φaT a^ =
√^1 2 π
6 η^ π
+ K+
π−^ − √^12 π^0 + √^16 η K^0 K−^ K 0 − √^26 η
(b) Notice I have kept the quark masses general. Calculate the masses of the mesons. Note the mass term is not diagonal; there is a π^0 η term. Calculate its coefficient, and what is it in the isospin limit?
(c) In the isospin limit, give a relation between the π, K, η masses-squared. This is the Gell-Mann– Okubo formula as applied to the octet of mesons (notice that here it involves relations among the squared-masses unlike what we found with the octet of baryons).
- [20 pts] Let’s now include the weak interactions inχPT. At low energies, we can “integrate out” the W bosons, giving us the Fermi interactions involving four quarks that we briefly discussed in class. One particular interaction that is often relevant is
∆L(8,1) = (sLdL)
q=u,d,s
(qLqL)
And this is labeled as such because it transforms as an octet (8) under the left-handed part of the SU (3) chiral symmetry, and a singlet (1) under the right-handed part. There of course is an overall coupling constant, but that is irrelevant for this process.
(a) Show that we can write this as
∆L(8,1) = (QLAQL)(QLQL)
where QT^ = (u, d, s), and determine what the matrix A is. (b) We would like to promote A to a spurion field as we did in class. Using the fact that under the SU (3)L × SU (3)R chiral symmetry
QL → LQL , QR → RQR , QL → QLL†^ , QR → QRR†^ ,
what would A have to transform like for this term to be invariant under the chiral symmetry? (c) There are two independent terms [with different Low-Energy Constants (LEC’s)] that arise at the chiral level for this Lagrangian at leading order [that are O(p^2 )]. Using Σ, Σ†, the mass matrix M, M †^ (which is also a spurion field with the transformation we discussed in class), A, and derivatives what would the chiral level terms be? Remember that the terms must also be invariant under the parity transformation Σ → Σ†. (d) This Lagrangian is one of the pieces that contributes to the nonleptonic decay of the kaon K^0 → π+π−, for example. Expand the Σ fields to cubic order to determine the Lagrangian in terms of the pions and kaons, and pick out the relevant terms for the K^0 → π+π−^ transition, calculate the amplitude and decay rate in terms of the LEC’s.
