Understanding One-Way ANOVA: Comparing Three or More Independent Means, Summaries of Economic statistics

Download Understanding One-Way ANOVA: Comparing Three or More Independent Means and more Summaries Economic statistics in PDF only on Docsity!

One-way between-subjects

ANOVA

Comparing three or more

independent means

ANOVA: A Framework

• Understand the basic principles of ANOVA
  • Why it is done?
  • What it tells us?
• Theory of one-way between-subjects ANOVA
• Following up an ANOVA:
  • Planned Contrasts/Comparisons
    • Choosing Contrasts
    • Coding Contrasts
  • Post Hoc Tests
• Writing up Results

One-Way ANOVA

• The one-way analysis of variance is used

to test the null hypothesis that three or

more population means are equal

• more precisely: test the null hypothesis that the means of the groups are not significantly different from the grand mean of all participants

One-Way ANOVA

• The response variable is the variable

you’re comparing, i.e., dependent variable

• The factor variable is the categorical

variable being used to define the groups,

i.e., independent variable

• Usually called k samples (groups)
• The one-way is because there is one

independent variable

The basic principle behind ANOVA Produces a test statistic termed the F-ratio Systematic Variance Unsystematic Variance If the model explains a lot more variability than it can’t explain, then the experimental manipulation has had a significant effect on the outcome (DV).

SST = based on differences between each data point and the grand mean SSM = differences between predicted values (group means) and the grand mean Grand Mean =

XPlacebo = 2. XLowDose = 3. XHighDose = 5. SSR = based on differences between person’s score and their group mean. Basis for SST Basis for SSR Basis for SSM Partitioning the Variance

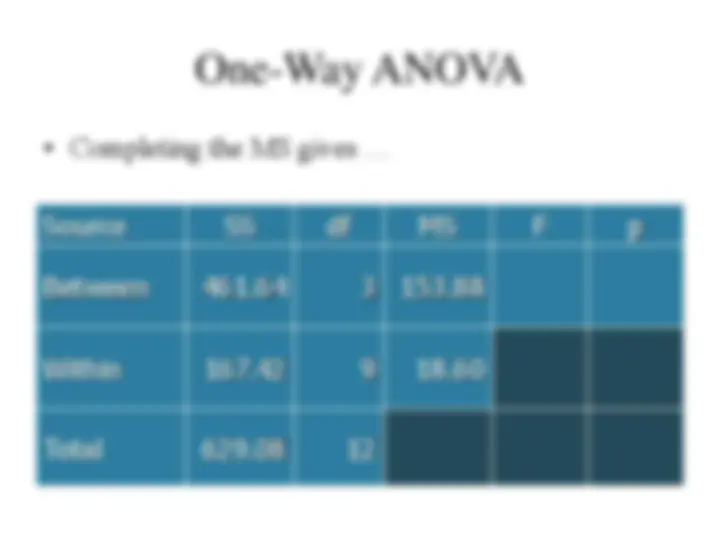
Mean Squares (MS M and MS R ) SSM = amount of variation explained by the model (exp. manipulation). SSR = amount of variation due to extraneous factors. These are “summed” scores and will therefore be influenced by the number of scores. To eliminate this bias we calculate the average sum of squares (mean squares) by dividing by the appropriate degrees of freedom. Calculating Degrees of Freedom (for one-way independent groups ANOVA) df total = N - 1 (number of all scores minus 1) dfM / between = k - 1 (number of groups minus 1) df (^) R / within = N - k (number of all scores minus number of groups)

The F-ratio

• We compare the amount of variability explained by the Model (MS M ), to the error in the model [individual differences] (MS R

• This ratio is called the F - ratio
• If the model explains a lot more variability than it can’t explain, then the experimental manipulation has had a significant effect on the outcome (DV). F = MS M MS R

An example: Fairness in different types of

societies

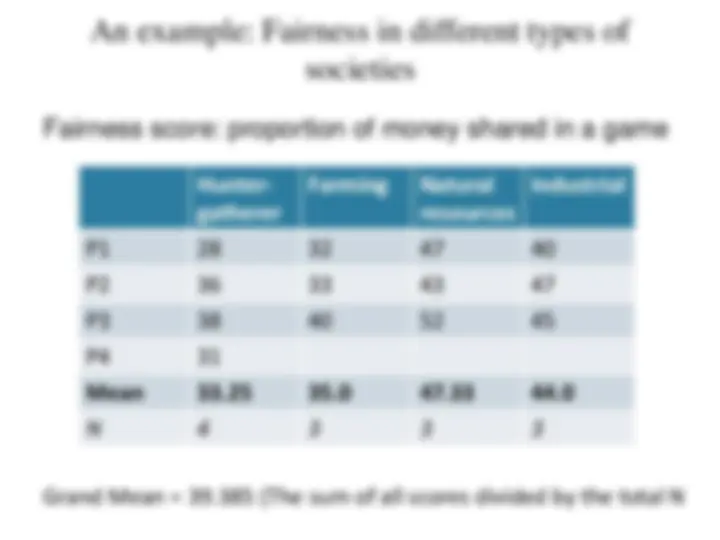
Fairness score: proportion of money shared in a game Hunter- gatherer Farming Natural resources Industrial P1 28 32 47 40 P2 36 33 43 47 P3 38 40 52 45 P4 31 Mean 33.25 35.0 47.33 44. N 4 3 3 3 Grand Mean = 39.385 (The sum of all scores divided by the total N

Total SS

The sum of the squared deviation of each score

from the grand total

2 ( )    T i grand SS x M

Model (between-group) sum of squares

(SS

M

1. Calculate the difference between the mean of each group and the grand mean. The grand mean is the mean of all scores
2. Square each of these differences
3. Multiply each result by the number of participants within that group
   • this is a correction (or “weighting”): a smaller sample will have less “weight” in the equation, a larger sample will have more “weight”.
4. Add the values for each group together. 2 ( )    M i i grand SS n M M

One-Way ANOVA

• After filling in the sum of squares, we have … Source SS df MS F p Between 461. Within 167. Total 629.

One-Way ANOVA

• Filling in the degrees of freedom gives this … Source SS df MS F p Between 461.64 3 Within 167.42 9 Total 629.08 12

Calculating the Mean Squares

Divide the SS by the corresponding df

• MS M

• MS R