Divideand
Conquer
Algorithms
COMP157
Sept212007
Prepare for your exams
Study with the several resources on Docsity
Earn points to download
Earn points by helping other students or get them with a premium plan
Guidelines and tips
Prepare for your exams
Study with the several resources on Docsity
Earn points to download
Earn points by helping other students or get them with a premium plan
Community
Ask the community
Ask the community for help and clear up your study doubts
University Rankings
Discover the best universities in your country according to Docsity users
Free resources
Our save-the-student-ebooks!
Download our free guides on studying techniques, anxiety management strategies, and thesis advice from Docsity tutors
Notes on Divide and Conquer Algorithms | COMP 157, Study notes of Algorithms and Programming
Material Type: Notes; Class: Design/Analysis of Algorithms; Subject: Computer Science; University: University of the Pacific; Term: Fall 2007;
Typology: Study notes
Pre 2010
1 / 35
This page cannot be seen from the preview
Don't miss anything!
Related documents
Partial preview of the text
Download Notes on Divide and Conquer Algorithms | COMP 157 and more Study notes Algorithms and Programming in PDF only on Docsity!
Divide
and
Conquer Algorithms
COMP
Sept
Divide
and
Conquer
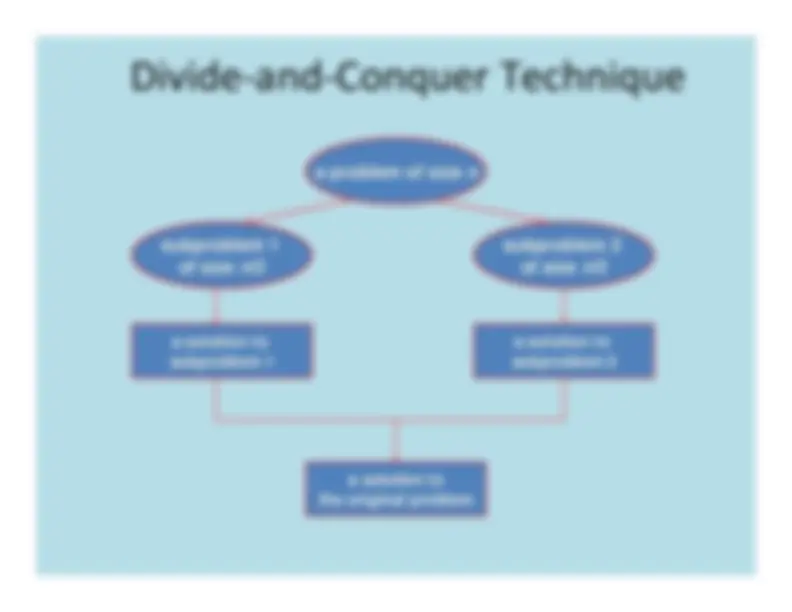
The
most
‐well
known
algorithm
design
strategy:
- Divide
instance
of
problem
into
two
or
more
smaller
instances
- Solve
smaller
instances
recursively
- Obtain
solution
to
original
(larger)
instance
by
combining
these
solutions
General Divide-and-Conquer Recurrence
T
n
aT
n/b
f
n
b = number of sub-problems
(usually 2)
a = number of sub-problems that need to be solved
(usually 2)
f(n) = cost of splitting problem +
cost of merging solutions to sub-problems
Divide-and-Conquer
Parallelization
T
n
aT
n/b
f
n
If we can concurrently solve all the sub-problems
(through parallel processing) , then a = 1.
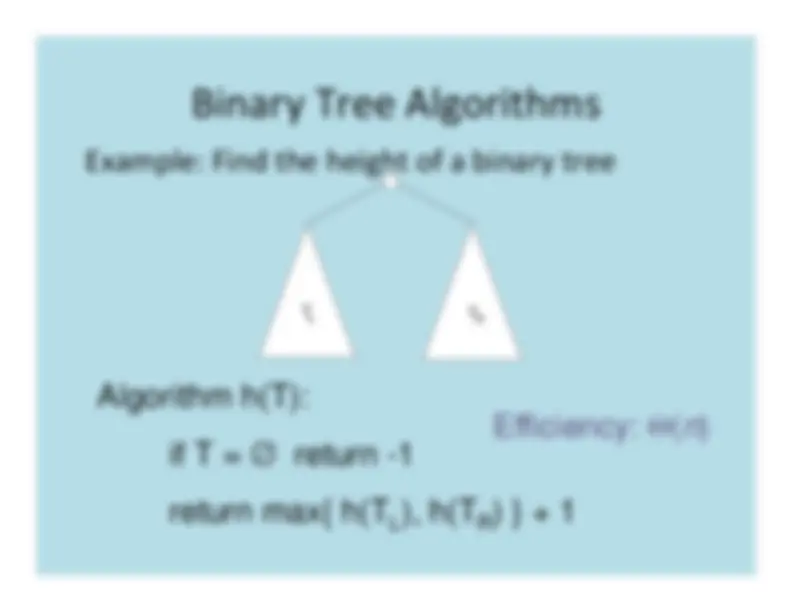
Master Theorem - Example
T
(
n
) = 2
T
( n
/2) +
^1
(recursive sum of array elements)
a = 2b = 2d = 0
Master Theorem: If
a > b
d
,^
T
(
n
)
∈ Θ
( n
log
b a
)
T
(
n
)
∈ Θ
( n
log
2 2
)
=
Θ
( n
)
Master Theorem - Example T
(
n
) = 4
T
(
n
/2) +
n
a = 4b = 2d = 1
Master Theorem: If
a > b
d
,^
T
(
n
)
∈ Θ
( n
log
b a
)
T
(
n
)
∈ Θ
( n
log
2 4
)
=
Θ
( n
2
)
Master Theorem - Example
T
(
n
) = 4
T
(
n
/2) +
n
3
a = 4b = 2d = 3
Master Theorem: If
a < b
d
,^
T
( n
)^
∈ Θ
(
n
d
)
T
(
n
)
∈ Θ
( n
3
)
Mergesort
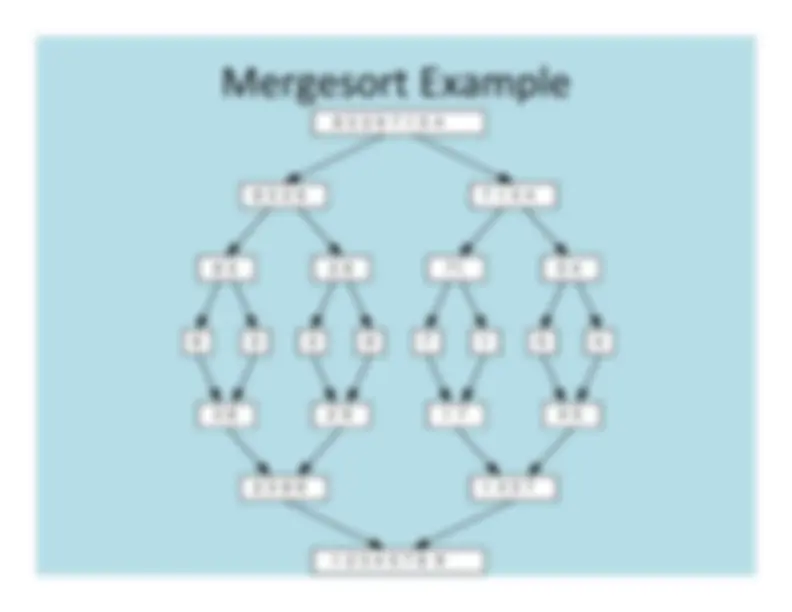
Split
array
A
into
two
(nearly)
equal
halves
and
make
copies
of
each
half
in
arrays
B
and
C
Sort
arrays
B
and
C
recursively
Merge
sorted
arrays
B
and
C
back
into
array
A
(next
slide)
Pseudocode
of
Mergesort
Pseudocode
of
Merge
Analysis
of
Mergesort
T(n)
2T(n/2)
n
a=2,
b=2,
d=
Master
Theorem: If
a
b
d
,^
T
( n
)^
( n
d
log
n
T
n
n
log
n
Analysis
of
Mergesort
All
cases
have
same
efficiency:
n
log
n
C
worst
(n)
n
log
2
n
n
which
is
close
to
theoretical
minimum:
⎡
log
2
n
!⎤
≈
n
log
2
n
‐^
n
(chapter
Space
requirement:
n
(not in
place)
(correct?)
Can
be
implemented
without
recursion
(bottom
up)
Partitioning
Algorithm
Analysis
of
Quicksort
Best
case:
split
in
the
middle:
n
log
n
Worst
case:
sorted
array:
n
2
Average
case:
random
arrays:
n
log
n
C
avg
(n)
n
log
2
n
Improvements:^ •
better
pivot
selection:
median
of
three
partitioning
-^
switch
to
insertion
sort
on
small
subfiles
-^
elimination
of
recursion
- switch
to
iteration
These
combine
to
20
‐25%
improvement