Understanding Number Systems: A Deep Dive into Binary, Octal, and Hexadecimal, Papers of Information Technology

Download Understanding Number Systems: A Deep Dive into Binary, Octal, and Hexadecimal and more Papers Information Technology in PDF only on Docsity!

L E C T U R E 7 New Mexico Tech: CS/IT 111

Binary Values &

Number Systems

CSI: Chapter 2 Goals

y New Mexico Tech: CS/IT 111

Categories of numbers

y

Positional notation

y

Conversion to and from base-

y

Binary, octal, and hexadecimal relationship

y

“Power of 2” bases and computing

First, a reminder …

y New Mexico Tech: CS/IT 111

Number

Unit belonging to an abstract mathematical system Subject to specified laws of succession, addition, multiplication

y

Natural numbers

Zero and any number obtained by repeatedly adding one to it

y

Negative numbers

A value less than 0, with a - sign

y

Integers

Natural numbers, negative numbers

y

Rational numbers

Integers and the quotient of two integers (fractions)

Natural Numbers

y New Mexico Tech: CS/IT 111

How many ones are there in 1337?

One thousand, three hundred and thirty-seven^ Ù

1 thousands

Ù

3 hundreds

Ù

3 tens

Ù

7 ones

But only in

base 10

y

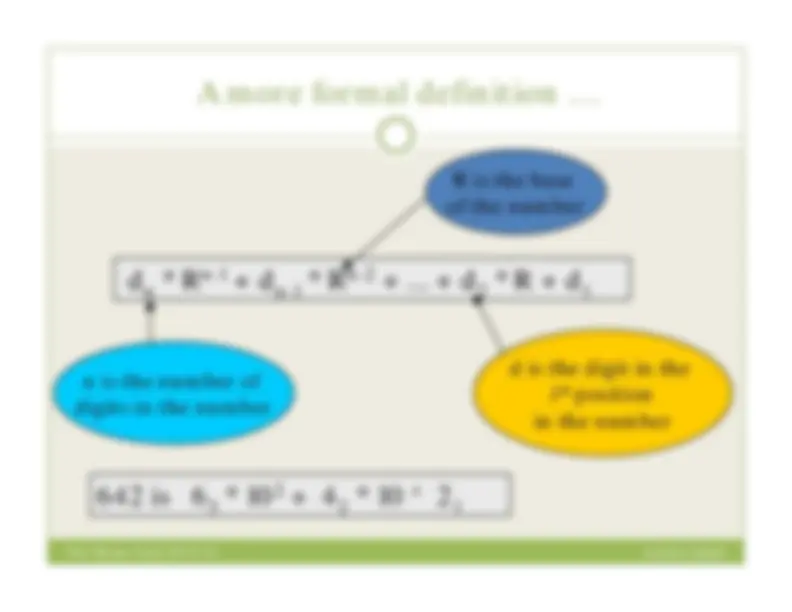
The base of a number determines the number of digits in the system and the value of the digitpositions.

What about bases higher than 10?

y New Mexico Tech: CS/IT 111

Digits are represented by distinct symbols fordecimal values 10 and above

Base 16: Hexadecimal^ Ù

{0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F}

A B C D E F 10 11 12 13 14 15

Positional Notation

y New Mexico Tech: CS/IT 111

Numbers are written using positional notation

y

In polynomial form:

x

3

x

2

x

1

x

0 Ù

Where

x

is the base

1 * 10 3 = 1 * 1000 = 1000

3 * 10 2 = 3 * 100 = 300

3 * 10 1 = 3 * 10 = 30

7 * 10 0 = 7 * 1 = 7 1337 This number is in base 10 The power indicates the position of the number

More Positional Notation

y New Mexico Tech: CS/IT 111

We’ve seen 1337 in base 10, what about another base?

Say 12 …

y

1337 12 is equivalent to 2275 10 1 * 12 3 = 1 * 1728 = 1728

3 * 12 2 = 3 * 144 = 432

3 * 12 1 = 3 * 12 = 108

7 * 12 0 = 7 * 1 = 7 2275

Arithmetic in Other Bases

02/02/

y New Mexico Tech: CS/IT 111

There’s nothing to be afraid of!

Same rules as base 10^ Ù

Carry

Ù

Borrow

1 1 1 1 1 1 1 0 1 0 1 1 1

1 0 0 1 0 1 1 1 0 1 0 0 0 1 0 1 2 2 0 2 1 0 1 0 1 1 1

1 1 1 0 1 1 0 0 1 1 1 0 0

“Power of 2” Number Systems

02/02/ Binary New Mexico Tech: CS/IT 111 Octal Hex Dec 0000 0 0 0 0001 1 1 1 0010 2 2 2 0011 3 3 3 0100 4 4 4 0101 5 5 5 0110 6 6 6 0111 7 7 7 1000 10 8 8 1001 11 9 9 1010 12 A 10 1011 13 B 11 1100 14 C 12 1101 15 D 13 1110 16 E 14 1111 17 F 15 A group of 4 binary digits can be converted into a single hexadecimal digit: So: 1 0 1 0 1 0 1 1 1 1 0 0 2 is ABC 16 1 0 1 0 1 0 1 1 1 1 0 0 A B C

Converting Decimal to Other Bases

y New Mexico Tech: CS/IT 111

An algorithm …

While (the quotient is not zero)^ Ù

Divide the decimal number by the new base

Ù

Make the remainder the next digit to the left in the answer

Ù

Replace the original decimal number with the quotient

y

What is 1988 10 in octal?

y

What is 3567 10 in hexadecimal?