Download Balanced Trees and Heaps: Multiway Search Trees, 2-3 Trees, Heaps and Heapsort and more Study notes Algorithms and Programming in PDF only on Docsity!

Balanced

Trees

and

Heaps

(Sections

COMP

Oct

Multiway Search

Trees

A

multiway search

tree

is

a

search

tree

that

allows

more

than

one

key

in

the

same

node

of

the

tree.

An

n

‐

node

contains

n

‐^1

ordered

keys

A

n

‐node

divides

the

key

range

into

n

intervals

(Ranges

for

the

node’s

n

subtrees)

k

1

<

k

2

<

k

3

[ k

, 1 k

2

)

< k

1

≥

k

n-

1

a 3-node

Tree

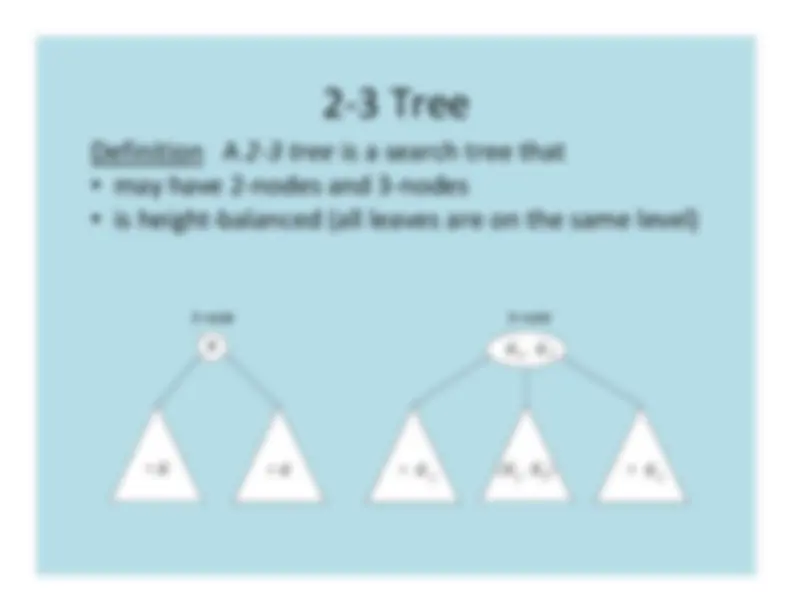
Definition

A

^2

‐^3

tree

is

a

search

tree

that

may

have

2

‐nodes

and

3

‐

nodes

is

height

‐balanced

(all

leaves

are

on

the

same

level)

K

K

,

K 1

2

( K

,

K

)

1

2

2-

node

3-

node

<

K

> K

<

K

K

1

2

Tree

Construction

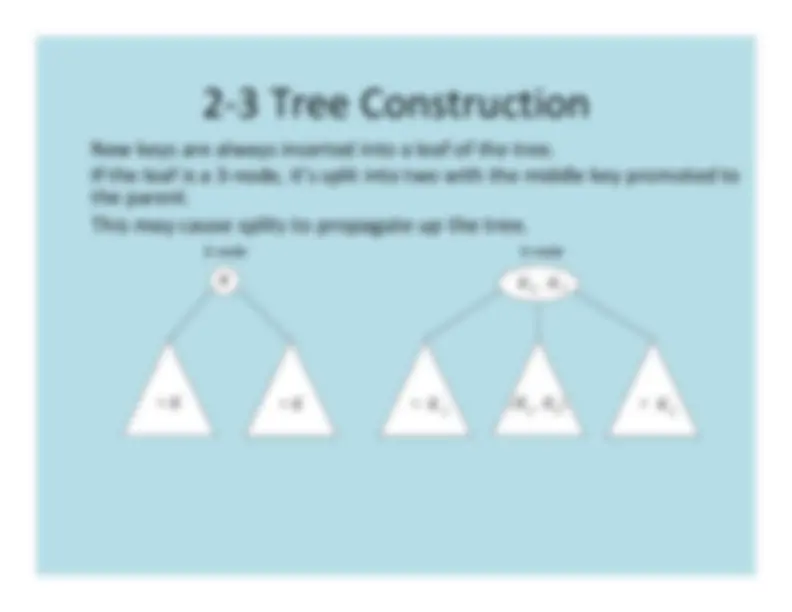
New

keys

are

always

inserted

into

a

leaf

of

the

tree.

If

the

leaf

is

a

3

‐node,

it’s

split

into

two

with

the

middle

key

promoted

to

the

parent.

This

may

cause

splits

to

propagate

up

the

tree.

K

K

,

K 1

2

( K

,

K

)

1

2

2-

node

3-

node

<

K

> K

<

K

K

1

2

Analysis

of

Trees

log

3

n

h

log

2

n

Search,

insertion,

and

deletion

are

in

(log

n

The

idea

of

tree

can

be

generalized

by

allowing

more

keys

per

node

2

‐^3

‐^4

trees

B

‐trees

Illustration

of

the

heap’s

definition

10

5

4

2

7

1

10

5

2

7

1

10

5

6

2

7

1

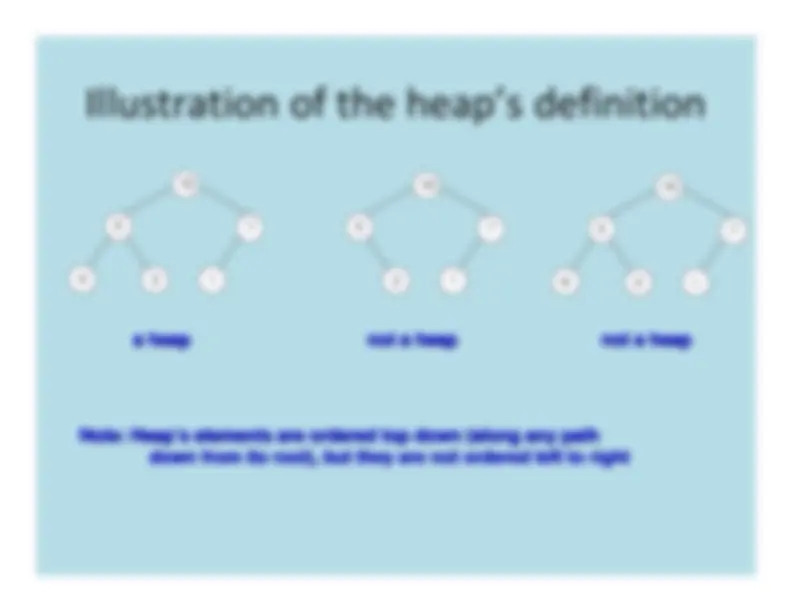
a heap^ a heap

not a heapnot a heap

not a heapnot a heap

Note: Heap’Note: Heap

’s elements are ordered top down (along any paths elements are ordered top down (along any path down from its root), but they are not ordered leftdown from its root), but they are not ordered left to right

to right

Important

Properties

of

a

Heap

There

exists

a

unique

binary

tree

with

n

nodes

that

is

essentially

complete,

with

h

log

2

n

The

root

contains

the

largest

key

The

subtree rooted

at

any

node

of

a

heap

is

also

a

heap

A

heap

can

be

represented

as

an

array

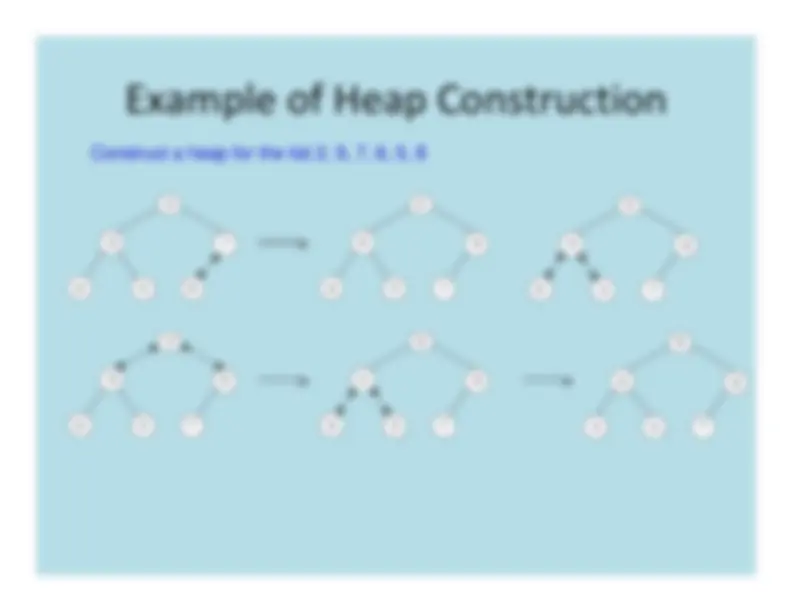
Step

0:

Initialize

the

structure

with

keys

in

the

order

given

Step

1:

Starting

with

the

last

(rightmost)

parental

node,

fix

the

heap

rooted

at

it,

if

it

doesn’t

satisfy

the

heap

condition:

keep

exchanging

it

with

its

largest

child

until

the

heap

condition

holds

Step

2:

Repeat

Step

1

for

the

preceding

parental

node

Heap

Construction

(bottom

up)

Example

of

Heap

Construction

7

2

9

6

5

8

2

9

6

5

8

7

2

9

6

5

8

7

2

9

6

5

8

7

9

2

6

5

8

7

9

6

2

5

8

7

Construct a heap for the list 2, 9, 7, 6, 5, 8

Stage

Construct

a

heap

for

a

given

list

of

n

keys

Stage

Repeat

operation

of

root

removal

n

times:

Exchange

keys

in

the

root

and

in

the

last

(rightmost)

leaf

Decrease

heap

size

by

1

If

necessary,

swap

new

root

with

larger

child

until

the

heap

condition

holds

Heapsort

Maximum

Key

Deletion

Exchange

root’s

key

with

last

key

in

heap.

Decrease

heap

size

by

Heapify the

smaller

tree

by

sifting

new

root

down

in

same

manner

as

bottom

up

construction

Step

of

heapsort repeats

this

until

heap

is

empty.

)) 1

(

log

( 2

(^2) )

( 2

2

(^10)

−

=

−

− =

n

n

i

h

h i

i

Stage

1:

Build

heap

for

a

given

list

of

n

keys

worst

‐case: C (

n

)^

=

C(n)

є

O(n)

Stage

2:

Repeat

operation

of

root

removal

n

‐^1

times

(fix

heap)

worst

‐case: C (

n

)^

=

C(n)

є

O(n log

n)

Both

worst

‐case

and

average

‐case

efficiency:

Θ

( n

log

n

)

In

‐place:

yes

Stability:

no

(e.g.,

1

nodes at level 1)

i

Analysis

of

Heapsort

−^1 =^1

2

log 2 n i

i