CS 340 - Introduction to Scientific Computing
Section 5.5: Adaptive Quadrature
The Idea: Using a composite integration technique with different subinterval widths (h) in order to
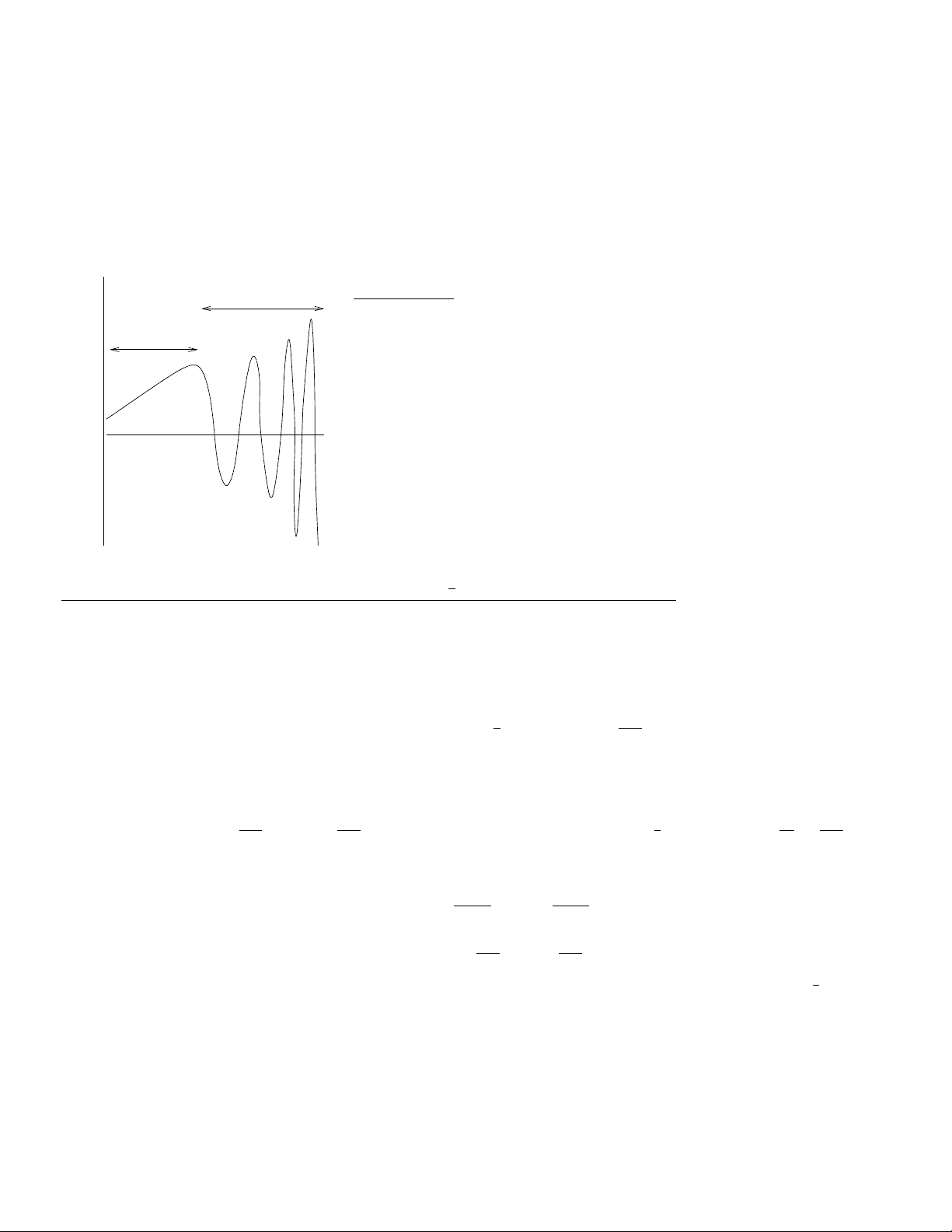
approximate the value of a definite integral, Rb
af(x)dx, correct to within a certain tolerance, ². Portions
of the f(x) curve with a large variation in values should require much smaller values of h, and portions of
the f(x) curve with little change in y-values would correspond to larger values of h. See the illustration
below.
Larger h−values
Less Variation
Smaller h−values
needed
More Variation
The Concept:
Approximate the integral over the initial interval.
Then approximate the integral over the left and right
half subintervals of that interval.
If the difference in the approximations for the area over
the original interval is less than the tolerance, STOP;
Return the sum of the integral over the two halves.
Otherwise, repeat this process, subdividing each of the new
subintervals.
The Adaptive Quadrature Process (with Simpson’s 1
3Rule and Error Tolerance ²):
Stage 1:
•Begin with the initial interval, [a,b]
•Define ²1=².
•Define S1[a, b] to be the results using Simpson’s 1
3rule with h1=b−a
2to approximate Rb
af(x)dx.
Stage 2:
•Cut the interval in half.
•Define S2ha, a+b
2iand S2ha+b
2, bito be the results of using Simpson’s 1
3rule with h2=h1
2=b−a
4
over the left and right half subintervals, respectively.
•Test if ¯
¯
¯
¯
S1[a, b]−µS2·a, a+b
2¸+S2·a+b
2, b¸¶¯
¯
¯
¯
< ²1
•If so, stop your subdividing. Let A2=S2ha, a+b
2i+S2ha+b
2, bibe your final result.
•If not, continue this halving process and repeat the same tests on each subinterval with ²2=1
2²1.
.
.
.
