Mixture Models-Introduction to Machine Learning-Lecture 16-Computer Science, Lecture notes of Introduction to Machine Learning

Download Mixture Models-Introduction to Machine Learning-Lecture 16-Computer Science and more Lecture notes Introduction to Machine Learning in PDF only on Docsity!

Lecture 16: Mixture models, EM

TTIC 31020: Introduction to Machine Learning

Instructor: Greg Shakhnarovich

TTI–Chicago

November 1, 2010

Review: generative models

General idea: assume (pretend?) p(x | y) comes from a certain parametric class, p(x | y; θy)

Estimate ̂θy from data in each class

Under this estimate, select class with highest p(x 0 | y; ̂θy)

Example: Gaussian model

• (^) Can make various assumptions regarding form and complexity of Gaussian covariance!

Plan for today

Semi-parametric models

the EM algorithm

Mixture models

So far, we have assumed that each class has a single coherent model.

−6−8 −6 −4 −2 0 2 4 6 8 10

−

−

0

2

4

6

8

10

Examples

Images of the same person under different conditions: with/without glasses, different expressions, different views.

Images of the same category but different sorts of objects: chairs with/without armrests.

Multiple topics within the same document.

Different ways of pronouncing the same phonemes.

Mixture models

Assumptions:

• (^) k underlying types (components);
• (^) yi is the identity of the component “responsible” for xi;
• yi is a hidden (latent) variable: never observed.

A mixture model:

−6^ −4 −4 −2 0 2 4 6 8

−

0

2

4

6

8

10

p(x; π) =

∑^ k

c=

p(y = c)p (x | y = c).

πc , p(y = c) are the mixing probabilities

We need to parametrize the component densities p (x | y = c).

Generative model for a mixture

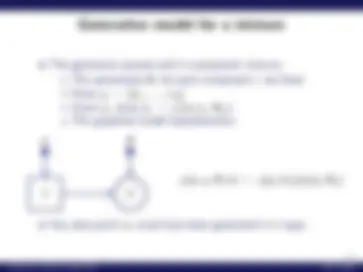
The generative process with k-component mixture:

• The parameters θc for each component c are fixed.
• (^) Draw yi ∼ [π 1 ,... , πk];
• (^) Given yi, draw xi ∼ p (x | yi; θyi ).
• The graphical model representation:

y (^) x

π θ

p(x, y; θ, π) = p(y; π)·p(x|y; θy)

Any data point xi could have been generated in k ways.

Gaussian mixture models

If the c-th component is a Gaussian, p (x | y = c) = N (x; μc, Σc), then

p(x; θ, π) =

∑^ k

c=

πc · N (x; μc, Σc) ,

where θ = [μ 1 ,... , μk, Σ 1 ,... , Σk].

The graphical model

y (^) x

π μ^1 ,...,k Σ^1 ,...,k

Mixture density estimation

Suppose that we do observe yi ∈ { 1 ,... , k} for each i = 1,... , N.

Let us introduce a set of binary indicator variables zi = [zi 1 ,... , zik] where

zic = 1 =

1 if yi = c, 0 otherwise.

The count of examples from c-th component:

Nc =

∑^ N

i=

zic.

Mixture density estimation: known labels

If we know zi, the ML estimates of the Gaussian components, just like in class-conditional model, are

−6^ −4 −4 −2 0 2 4 6 8

−

0

2

4

6

8

10 y=

y=

π̂ c =

Nc N

μ̂ c =

Nc

∑N

i=

zicxi,

Σ̂ c = 1 Nc

∑N

i=

zic(xi − μ̂ c)(xi − ̂μc)T^.

Expected likelihood

The “complete data” likelihood (when z are known):

p(X, Z; π, θ) ∝

∏^ N

i=

∏^ k

c=

(πcN (xi; μc, Σc))zic^.

and the log:

log p(X, Z; π, θ) = const +

∑^ N

i=

∑^ k

c=

zic (log πc + log N (xi; μc, Σc)).

We can’t compute it, but can take the expectation w.r.t. the posterior of z, which is just γic:

Ezic∼γic [log p(xi, zic; π, θ)].

Expected likelihood

log p(X, Z; π, θ) = const +

∑^ N

i=

∑^ k

c=

zic (log πc + log N (xi; μc, Σc)).

Expectation of zic:

Ezic∼γic [zic] =

z∈ 0 , 1

z · γicz = γic.

The expected likelihood of the data:

Ezic∼γic [log p(X, Z; p, θ)] = const

∑^ N

i=

∑^ k

c=

γic (log πc + log N (xi; μc, Σc)).

Summary so far

If we know the parameters and indicators (assignments) we are done.

If we know the indicators but not the parameters, we can do ML estimation of the parameters – and we are done.

If we know the parameters but not the indicators, we can compute the posteriors of indicators;

• With known posteriors, we can estimate parameters that maximize the expected likelihood – and then we are done.

But in reality we know neither the parameters nor the indicators.

The EM algorithm

Start with a guess of θ, π.

• Typically, random θ and πc = 1/k.

Iterate between: E-step Compute values of expected assignments, i.e. calculate γic, using current estimates of θ, π. M-step Maximize the expected likelihood, under current γic.

Repeat until convergence.