Download Automatic Mid-Sagittal Plane and Surface Localization in Brain Imaging and more Exercises Medical imaging in PDF only on Docsity!
Mid-sagittal Plane and Mid-sagittal Surface Optimization in
Brain MRI Using a Local Symmetry Measure
Mikkel B. Stegmanna,b, Karl Skoglunda,b, Charlotte Rybergb
aInformatics and Mathematical Modelling, Technical University of Denmark,
Richard Petersens Plads, Building 321, DK-2800 Kgs. Lyngby, Denmark
bDanish Research Centre for Magnetic Resonance,
Copenhagen University Hospital Hvidovre, Ketteg˚ard All´e 30, DK-2650 Hvidovre, Denmark
ABSTRACT
This paper describes methods for automatic localization of the mid-sagittal plane (MSP) and mid-sagittal sur- face (MSS). The data used is a subset of the Leukoaraiosis And DISability (LADIS) study consisting of three- dimensional magnetic resonance brain data from 62 elderly subjects (age 66 to 84 years). Traditionally, the mid-sagittal plane is localized by global measures. However, this approach fails when the partitioning plane between the brain hemispheres does not coincide with the symmetry plane of the head. We instead propose to use a sparse set of profiles in the plane normal direction and maximize the local symmetry around these using a general-purpose optimizer. The plane is parameterized by azimuth and elevation angles along with the distance to the origin in the normal direction. This approach leads to solutions confirmed as the optimal MSP in 98 percent of the subjects. Despite the name, the mid-sagittal plane is not always planar, but a curved surface resulting in poor partitioning of the brain hemispheres. To account for this, this paper also investigates an opti- mization strategy which fits a thin-plate spline surface to the brain data using a robust least median of squares estimator. Albeit computationally more expensive, mid-sagittal surface fitting demonstrated convincingly better partitioning of curved brains into cerebral hemispheres.
1. INTRODUCTION
The human brain consists on a coarse level of the cerebrum, the cerebellum and the brainstem. Most prominent is the cerebrum which is divided into hemispheres, connected by the nervous fiber bundle called the corpus callosum. The surface partitioning this approximate bilateral symmetry of the cerebrum is typically denoted the mid-sagittal plane (MSP) referring to its relative alignment with the sagittal plane of the human body.
Knowing the exact location of this surface has many applications. One is to provide the first step in spatial normalization or anatomical standardization of brain images.1–3^ Another is to provide means for estimating the departures from bilateral symmetry in the cerebrum1, 4–6^ often seen in pathological brains.^5
Finally, determining the MSP is an invariable prerequisite for measurements on structures defined via this plane such as the MSP cross-section of the corpus callosum. A structure particularly interesting due to the many neurological studies indicating relationships between the size and shape of the corpus callosum, and gender, age, neurodegenerative diseases et cetera.7–9^ MSP estimation can thus be viewed as a step prior to automated corpus callosum morphometry (cf.7, 10–12).
This paper presents two inherently three-dimensional methods for automatic localization of this partitioning surface using direct optimization of a local symmetry measure. Insisting on local symmetry contrary to global, which is the typical approach to MSP estimation, enables determination of brain symmetry that departs from head symmetry. The first method parameterizes a mid-sagittal plane and optimizes symmetry using the well- known Nelder-Mead simplex optimization scheme. The second utilizes results from robust statistics to fit a mid-sagittal surface (MSS) parameterized by thin-plate kernel functions. The efficacy of both methods is eval- uated on magnetic resonance scans of a cohort of 62 elderly subjects, obtained from the pan-European LADIS study.^13
Corresponding author is M. B. Stegmann, E-mail: mbs@imm.dtu.dk, Web: http://www.imm.dtu.dk/∼mbs/.
2. RELATED WORK
Several papers have dealt with MSP estimation. The bulk part treats the problem as an optimization of global symmetry2, 3, 5, 14–17^ resulting in solutions dominated by the skull shape. However, Ardekani et al.^1 modified a global solution by introducing a thresholding approach aiming at excluding background and parts with non- overlapping skull.
Although being a truly three-dimensional problem, some choose to seek solutions in a two-dimensional fashion5, 6 and later fusing these into a global solution, occasionally depending on various thresholds and other parameters that are hard to choose (see e.g. ref^6 ). We note that two-dimensional approaches induce an implicit requirement of having 2D image slices with near-orthogonal orientation with respect to the MSP.
To the best of our knowledge, all previous approaches, but two, models the partitioning surface between the cerebral hemispheres as a plane. Christensen et al.^18 and Darvann et al.^19 assess dysmorphologies using the craniofacial MSP modeled as a thin-plate spline surface. Aiming at measuring craniofacial rather than brain asymmetry in infants with unilateral coronal craniosynostosis, this surface was fitted directly to landmark points placed manually on computed tomography scans of the skull.
3. DATA MATERIAL
The data material used in this study comprises 62 magnetic resonance images (MRI) of the human brain obtained from 62 elderly subjects (age 66 to 84 years) using a whole body MR scanner; Siemens Vision 1.5 Tesla. All subjects originated from a subset of the LADIS study^13 (Leukoaraiosis and Disability in the Elderly). MR pulse sequence: MPRAGE; matrix size: 256×256 pixels; field of view: 250× 250 ×150 mm (voxel size: 0.997×0.977×1. mm). A method for automatically locating the corpus callosum has previously been reported on a subset of the data set mentioned above .12, 20
4. METHODS
As not all literature is in consensus regarding the understanding of the mid-sagittal plane and surface, we will make these issues explicit by providing the following definitions:
Definition 4.1. The mid-sagittal plane (MSP) is the planar surface which bisects the cerebrum into two cerebral hemispheres at their point of bilateral symmetry.
Definition 4.2. The mid-sagittal surface (MSS) is the general surface which separates the cerebrum into two cerebral hemispheres at their point of bilateral symmetry.
It follows that the MSP and MSS must be placed exactly in the center of the inter-hemispheric fissure. This eliminates the extra degrees of freedom introduced in subjects with widened longitudinal fissures, and yields a unique MSP and MSS.
4.1. Mid-sagittal Plane Estimation
Due to the definition above, MSP estimation strategies based on global measures of symmetry must be rejected. This work is concerned about brain partitioning, rather than head symmetry. To avoid the complex, laborious and orientation-dependent methods induced by a slice-based approach to MSP estimation, the problem is cast into a standard optimization framework, requiring a suitable parameterization, a cost-function and an efficient optimizer. The parameterization should uniquely determine the orientation and position of the MSP, and the cost-function should estimate the local symmetry around the MSP.
4.2. Mid-sagittal Surface Estimation
The mid-sagittal plane estimate is satisfyingly accurate for the great majority of subjects. Furthermore, in technical applications, it is reasonable to believe that planar cross-sections of the brain are favored. Nevertheless, a few of the patients in the present data set exhibit a slight but clearly visible bending along the entire mid- sagittal fissure, or, in some cases, a more prominent bending of the occipital lobe, proximal to the cerebellum (the so-called torque effect^15 ). The optimal MSP cannot accurately represent the mid-sagittal surface (MSS, see Definition 4.2) in these cases. As shown by,^18 a curved MSS may also be a result of craniofacial dysmorphologies. To account for these cases, we have investigated the possibility of fitting a surface instead of a plane using a similar symmetry measure as described above.
4.2.1. Surface Representation
Thin-plate splines are a natural choice of surface representation, since we are interested in capturing global curvature trends of the MSS. Thin-plate splines are able to contain such information using a low number of control points. The following basic description of thin-plate splines stems from.^22
A single thin-plate spline is the solution to the mechanical problem of finding the shape of an infinitely large and thin metal plate, minimizing its bending energy subject to interpolation of height values y = f (x, z).
f (x, z) = a 1 + axx + az z +
∑^ p
i=
wiU (‖(xi, zi) − (x, z)‖) (7)
Here, p is the number of knots, (xi, zi) on the two-dimensional manifold spanned by the imaginary steel plate. The corresponding values yi can be interpreted as height values at the knots. U (‖(xi, zi) − (x, z)‖) is the basis function U (r) = r^2 log r, U (0) = 0. It can be shown that this choice leads to minimal plate bending energy.^24 The thin-plate spline consists of an affine part determined by the coefficients a 1 , ax and az and a non-affine part where {wi|i = 1... p} is a set of weights. We require that
∑^ p
i=
wi =
∑^ p
i=
wixi =
∑^ p
i=
wizi = 0 (8)
Since the thin-plate spline is an interpolant, we also have the p conditions yi = f (xi, zi). These conditions can be arranged in a linear system as (^) [ K P PT^ O
] [
w a
]
[
y o
]
where Kij = U (‖(xi, zi) − (xj , zj )‖), the ith row of P is (1, xi, zi), O and o are the 3 × 3 and 3 × 1 zero matrices respectively, and w, y and a are column vectors formed from wi, yi and the affine coefficients. The design matrix in the linear system above is nonsingular provided that K is invertible,^24 and the system can thus be solved by matrix inversion. A regularization term λ can be added so that the spline approximates the data points instead of interpolating them. This lowers the bending energy of the system. This is performed by changing K into K + λI, where I is the p × p identity matrix.
The physical properties of the thin-plate spline suit our purposes fine. It will interpolate or approximate any points that have been found to lie on a potential MSS, without introducing excessive bending or sudden kinks in the surface.
The principal idea of the spline fitting algorithm is to first gather a set of data points in R^3 which represents the mid-sagittal surface. Among these points, there will be many outliers. The spline is therefore fitted to data in a robust fashion.
4.2.2. Extraction of MSS Data Points
Assuming that the brain data is roughly aligned, it is possible to find reasonably accurate estimations of points on the MSS by finding the maximal local symmetry in a slice-by-slice, scanline fashion. Restricting the search to slices roughly containing the entire cerebrum, data points are found in the following way.
Algorithm 1 MSS Data Extraction 1: for each slice do 2: for each scale do 3: for each line do 4: Slide a profile (of width k) s pixels across the midpoint: 5: for each position do 6: Compute the correlation coefficient between the first half of the profile 7: and a mirrored version of the second half 8: Measure the image intensity at the profile’s center pixel 9: Combine the two measurements, keep track of the result 10: end for 11: Choose the position having the highest score 12: end for 13: end for 14: Average the results from each scale 15: end for
Here, four Gaussian scales are used with σ = { 1 , 2 , 3 , 4 } and corresponding profile widths of k = { 15 , 23 , 33 , 43 } pixels. The search width s is s = 25 pixels. The image intensity is transformed to [0... 1] and is weighted equally with the symmetry measure as the two are combined. To reduce the number of irrelevant and erroneous measurements, for instance points outside the cranium, values with a low symmetry measure as well as profiles with low variation are not considered.
The method described above assumes that the scans are roughly aligned. We have also investigated the possibility of maximizing local symmetry along profiles normal to the optimal MSP; however, the results were comparable. The scanline algorithm was therefore favored since it is more foreseeable and easier to implement.
4.2.3. Robust Spline Fitting
As the MSS data is heavily contaminated with outliers, a regular optimization algorithm or regression technique cannot be expected to perform well. Some robust method, capable of handling a large proportion of noise, is therefore needed. Such methods are for instance regression diagnostics, M-estimators, RANSAC and least median of squares.^25 In this project, the least median of squares (LMedSq) method is used since it applies well to spline fitting and is capable of handling up to 50 % outliers.^25 LMedSq solves the nonlinear minimization problem min med i r i^2 (10)
where ri denotes the ith residual. Unfortunately, there is no direct solution to this problem. To find the global minimum, an exhaustive search through the entire search space must be performed. For n data points, there are
mtot =
n p
ways to choose p points; a number that renders this strategy infeasible in most cases. The common
way to overcome this is by considering a selected number m ø mtot of samples of p points each. Before we get into details of the algorithm, let’s see how it is applied here.
We wish to construct a spline that interpolates or approximates a selected number of control points from our set of data points. To rectify the coordinate system, the data is first rotated according to a least-squares plane fit The data is roughly planar and the rotation aligns it with the coordinate axes. The in-plane axes are interpreted the xz-plane used in Equation 7. The data points’ deviations from the plane are interpreted as the control points yi. Following the LMedSq algorithm, we wish to find a sample from the data points that produces a spline that gives the lowest possible squared median distance with regards to all data points. The number of data points p to include in each sample is hard to estimate, since we don’t have any prior knowledge of the complexity of the MSS. This could be acquired from a training set of mid-sagittal surfaces. Experiments show that choosing between 5 and 9 produces accurate results, and is a reasonable trade-off between low surface complexity and specificity. The remaining question is how to estimate m, the number of random samples to draw. A sample of
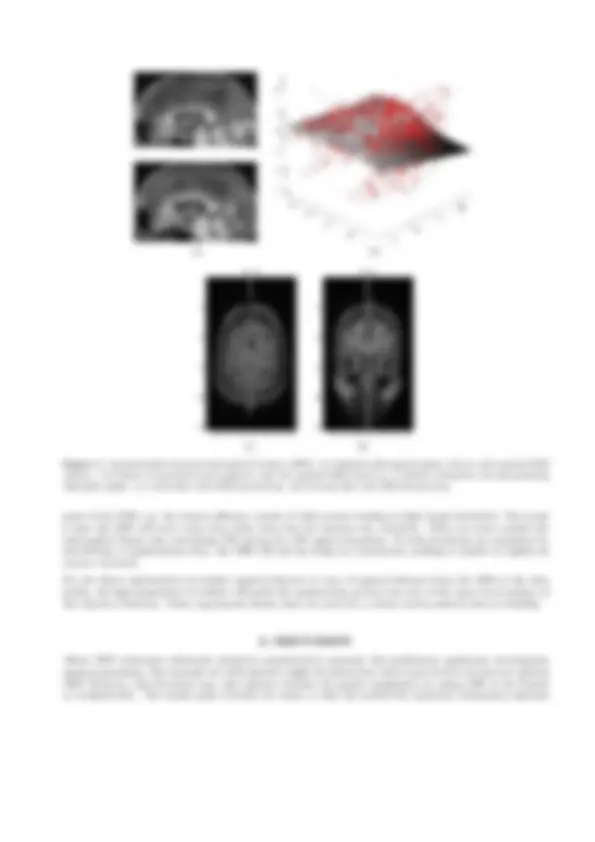
Figure 1. Initial mid-sagittal planes for all 62 subjects (shown row-wise).
Figure 2. Optimal mid-sagittal planes for all 62 subjects (shown row-wise).
(a) (b)
Slice 199
20 40 60 80 100 120 140
50
100
150
200
250
(c)
Slice 59
20 40 60 80 100 120 140
50
100
150
200
250
(d)
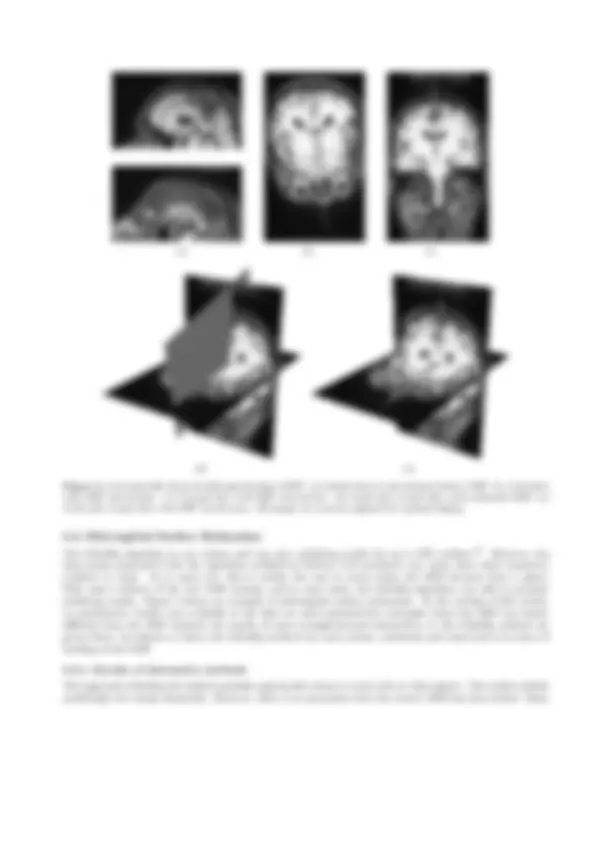
Figure 4. Automatically detected mid-sagittal surface (MSS). (a) Optimal mid-sagittal plane (above) and optimal MSS (below). (b) Points of maximal local symmetry and the optimal MSS based on a robustly estimated, non-interpolating thin-plate spline. (c) Axial slice with MSS intersection. (d) Coronal slice with MSS intersection.
parts of the MSS, e.g. the corpus callosum, consist of white matter leading to high image intensities. The result is that the MSS will move away from these areas into for instance the ventricles. These are areas outside the mid-sagittal fissure also containing CSF giving low MR signal intensities. If such deviations are penalized by introducing a regularization term, the MSS will end up being too constricted, yielding it unable to explain its correct curvature.
For the direct optimization of median squared distance or sum of squared distance from the MSS to the data points, the high proportion of outliers will guide the optimization process into one of the many local minima of the objective function. These experiments clearly show the need for a robust search method such as LMedSq.
6. DISCUSSION
Albeit MSP estimation ultimately should be quantitatively assessed, this preliminary qualitative investigation appears promising. One example out of 62 showed a slight deviation from what is perceived to be the true optimal MSP. However, this deviation may only indicate whether the grader emphasizes on seeing CSF in the frontal or occipital lobe. The results point towards two issues, i) that the method for symmetry estimation expresses
the features wanted in a good MSP estimation, and ii) the optimization approach is stable and accurate in a reasonable large test set. The latter indicates that the proposed method is capable of dealing with typical clinical variation in in-scanner head alignment.
The proposed approach is inherently three-dimensional, conceptually simple and straight-forward to implement. The only independent parameters are the normal width and the normal spacing. In the event of having images with permuted orientation (e.g. coronal and sagittal image slices interchanged) a standard principal axes ini- tialization has been recommended. Due to the local symmetry measure this method is insensitive to partially cropped brains unlike global methods, which heavily relies on the entire head to be scanned. Further, relying on local symmetry rather than the presence of cerebral spinal fluid (CSF) should enable this method to deal with severe variability in inter-hemispheric fissure width, e.g. due to atrophy.^6 An informal investigation of the fissure width in the present data set supported this observation. In addition, the symmetry approach renders the method insensitive to the choice of MR scanning protocol.
However, the advantages of using a local symmetry come at a cost. Images generated with a very wide impulse- response function (thus having very limited high-frequency content) such as functional SPECT and PET images, will not show any pronounced local symmetry at the inter-hemispheric fissure. For such images our approach will fail. Consequently, the MSP can in such cases only be estimated by educated guesses from global measures such as skull symmetry, regardless of non-coinciding brain and head symmetry and torque effects causing the partitioning surface to curve.^15
There may be doubt about the usefulness of a mid-sagittal surface. For instance, varying curvature of a slice will lead to varying geometric properties, making comparisons and statistical analysis complicated. However, a plane approximation of a curved MSS will result in a partly misplaced cross-section. In effect, there is a trade-off between the complexity of the MSS and the limited accuracy of the MSP.
The LMedSq algorithm works well and is easy to understand and implement. Regarding the complexity of the problem it solves, it has relatively few free parameters that need tuning. However, more results are needed to complete the preliminary findings reported in this paper.
7. CONCLUSION
This paper presented two inherently three-dimensional and novel approaches to estimation of the surface par- titioning the hemispheres of the cerebral brain at their point of approximate bilateral symmetry. Contrary to most literature, these employed a local symmetry measure and included partitioning functions being planar as well as general surfaces. Both have been qualitatively validated in a cohort of 62 elderly subjects with encour- aging results. Future work will concentrate on assessing their efficiency quantitatively by using synthetic brain data supplemented by manual gold standard measurements on actual MRI. Sensitivity studies with respect to pathologies (e.g. space-occupying lesions), field inhomogeneity and image noise should also be carried out to fur- ther validate the current results. The road ahead for mid-sagittal surface extraction contains a mix of sampling a direct optimization to increase efficiency, and an integration of the data point extraction and the search.
Acknowledgements
The work of M. B. Stegmann was supported by The Danish Medical Research Council, grant no. 52-00-0767, and The Danish Research Agency, grant no. 2059-03-0032. Karl Skoglund was supported by The Technical University of Denmark, DTU. Charlotte Ryberg was supported by The Velux Foundation, Denmark.
REFERENCES
- B. Ardekani, J. Kershaw, M. Braun, and I. Kanuo, “Automatic detection of the mid-sagittal plane in 3-D brain images,” IEEE Transactions on Medical Imaging 16 (6), pp. 947–52, 1997.
- A. V. Tuzikov, O. Colliot, and I. Bloch, “Brain symmetry plane computation in MR images using inertia axes and optimization,” Pattern Recognition, 2002. Proceedings. 16th International Conference on 1 , pp. 516–519 vol.1, 2002.
