




























Study with the several resources on Docsity

Earn points by helping other students or get them with a premium plan


Prepare for your exams
Study with the several resources on Docsity

Earn points to download
Earn points by helping other students or get them with a premium plan
Community
Ask the community for help and clear up your study doubts
Discover the best universities in your country according to Docsity users
Free resources
Download our free guides on studying techniques, anxiety management strategies, and thesis advice from Docsity tutors
The Method of Sections is an engineering technique used to analyze the static equilibrium of truss structures. By cutting the truss into sections and solving for the equilibrium of each section, unknown forces can be determined. This document demonstrates the application of the Method of Sections through various examples.
What you will learn
Typology: Slides
1 / 46

This page cannot be seen from the preview
Don't miss anything!







































◮ (^) The Method of Sections involves analytically cutting the truss into sections and solving for static equilibrium for each section.
◮ (^) The Method of Sections involves analytically cutting the truss into sections and solving for static equilibrium for each section. ◮ (^) The sections are obtained by cutting through some of the members of the truss to expose the force inside the members.
◮ (^) The Method of Sections involves analytically cutting the truss into sections and solving for static equilibrium for each section. ◮ (^) The sections are obtained by cutting through some of the members of the truss to expose the force inside the members. ◮ (^) In the Method of Joints, we are dealing with static equilibrium at a point. This limits the static equilibrium equations to just the two force equations. A section has finite size and this means you can also use moment equations to solve the problem. This allows solving for up to three unknown forces at a time. ◮ (^) Since the Method of Sections allows solving for up to three unknown forces at a time, you should choose sections that involve cutting through no more than three members at a time.
◮ (^) The Method of Sections involves analytically cutting the truss into sections and solving for static equilibrium for each section. ◮ (^) The sections are obtained by cutting through some of the members of the truss to expose the force inside the members. ◮ (^) In the Method of Joints, we are dealing with static equilibrium at a point. This limits the static equilibrium equations to just the two force equations. A section has finite size and this means you can also use moment equations to solve the problem. This allows solving for up to three unknown forces at a time. ◮ (^) Since the Method of Sections allows solving for up to three unknown forces at a time, you should choose sections that involve cutting through no more than three members at a time. ◮ (^) When a member force points toward the joint it is attached to, the member is in compression. If that force points away from the joint it is attached to, the member is in tension.
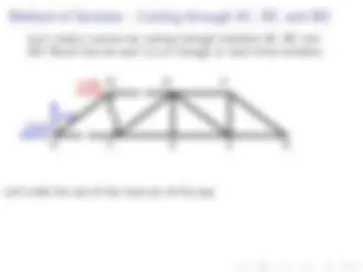
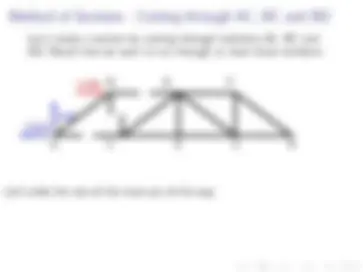
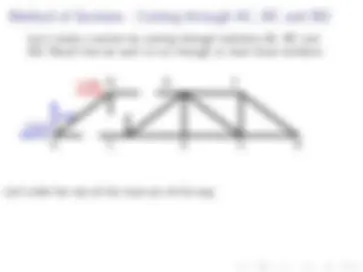
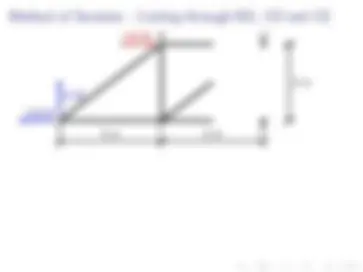
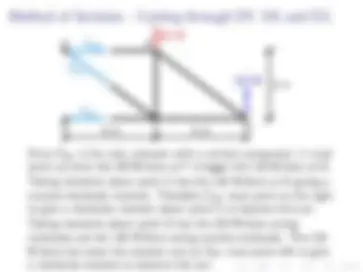
Let’s create a section by cutting through members AC, BC and BD. Recall that we want to cut through at most three members.
4m 4m 4m 4m
3m
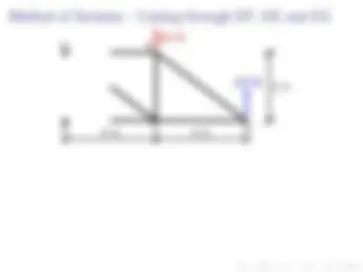
Let’s create a section by cutting through members AC, BC and BD. Recall that we want to cut through at most three members.
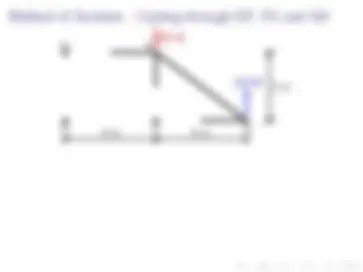
Let’s slide the rest of the truss out of the way.
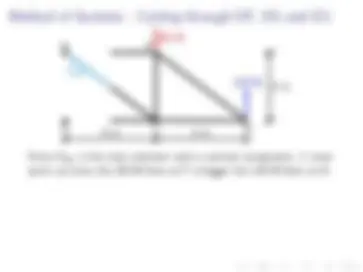
Let’s create a section by cutting through members AC, BC and BD. Recall that we want to cut through at most three members.
Let’s slide the rest of the truss out of the way.
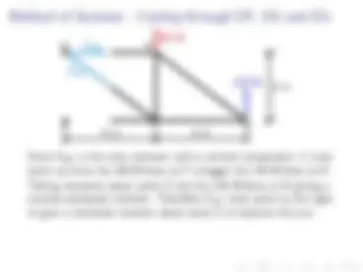
Let’s create a section by cutting through members AC, BC and BD. Recall that we want to cut through at most three members.
Let’s slide the rest of the truss out of the way.
Let’s create a section by cutting through members AC, BC and BD. Recall that we want to cut through at most three members.
b
(^) b
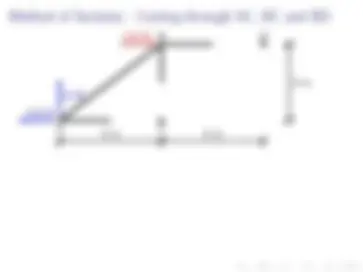
Let’s redraw this section enlarged.
120 N (^) b
b
4 m 4 m
3 m
120 N (^) b
b
4 m 4 m
3 m
FBC FAC
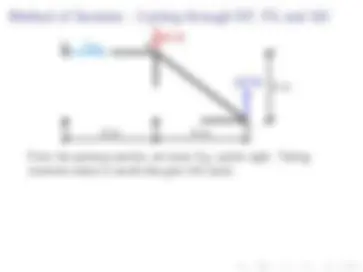
Since FBC is the only force that has a vertical component, it must point down to balance the 15 N force (Ay ). Taking moments about point B has both forces at A giving clockwise moments. Therefore, FAC must point to the right to provide a counter-clockwise moment.
120 N (^) b
b
4 m 4 m
3 m
FBC FAC
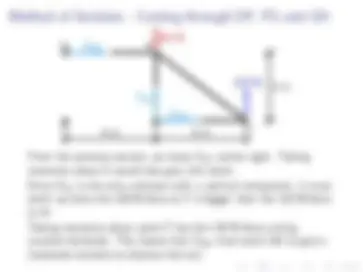
Since FBC is the only force that has a vertical component, it must point down to balance the 15 N force (Ay ). Taking moments about point B has both forces at A giving clockwise moments. Therefore, FAC must point to the right to provide a counter-clockwise moment. Taking moments about point C has the 15 N force acting at A and the 120 N acting at B giving clockwise moments. Therefore, FBD must point to the left to provide a counter-clockwise moment.
Solving in the order of the previous page:
↑ +^
Fy = +15N − FBC = 0
FBC = 15N (tension)
(360 + 60)Nm 3 m
= 140N (tension)
Solving in the order of the previous page:
↑ +^
Fy = +15N − FBC = 0
FBC = 15N (tension)
(360 + 60)Nm 3 m
= 140N (tension)
(60 + 360)Nm 3 m
= 140N (compression)