maquinas termicas, segunda ley, Schemes and Mind Maps of Innovation

Download maquinas termicas, segunda ley and more Schemes and Mind Maps Innovation in PDF only on Docsity!

La Segunda Ley de la Termodinámica establece una dirección para los procesos energéticos y define los límites del aprovechamiento de la energía térmica. A diferencia de la Primera Ley, que se enfoca en la conservación de la energía, la Segunda Ley introduce el concepto de irreversibilidad y entropía, señalando que no toda la energía puede transformarse en trabajo útil. Esta ley es fundamental para el estudio de las máquinas térmicas, dispositivos que convierten parte del calor absorbido desde una fuente caliente en trabajo mecánico, mientras liberan el resto del calor a una fuente fría. Las máquinas térmicas, como los motores de combustión interna o las plantas termoeléctricas, operan cíclicamente y están sujetas a un límite teórico de eficiencia impuesto por el ciclo de Carnot. El análisis de estas máquinas a través de la Segunda Ley permite entender por qué existen pérdidas energéticas inevitables y cómo se puede optimizar su funcionamiento dentro de los márgenes impuestos por la naturaleza.

𝑇 1 = 477 °𝐶 = 750. 15 °𝐾 𝑇2 = 25 °𝐶 = 298. 15 °𝐾 𝑄𝑖𝑛= 65 000 𝑘𝐽/ min = 1 083 333. 33 𝑊 η = 1 − 𝑇 2 𝑇 1 η = 1 −

298. 15 𝑇 1750. 15 η = 0. 6024 100% η = 60 .24% 𝑊𝑚𝑎𝑥 = η ∗ 𝑄𝑖𝑛 𝑊𝑚𝑎𝑥 = 0. 6024 ∗ 1 083 333. 33 𝑊𝑚𝑎𝑥 = 652. 500 𝑊

η = 1 − 𝑇𝑠𝑢𝑚 𝑇𝑓𝑢𝑒𝑛𝑡𝑒 η = 1 −

273. 15
274. 15 η = 0. 6359 ∗ 100% η = 63 .59% 𝑊𝑚𝑎𝑥 = η ∗ 𝑄𝑖𝑛 𝑊𝑚𝑎𝑥 = 0. 6359 ∗ 1 083 333. 33 𝑊𝑚𝑎𝑥 = 688 862. 23 W η = 1 − 𝑇𝑠𝑢𝑚 𝑇𝑓𝑢𝑒𝑛𝑡𝑒 η = 1 −
275. 15
276. 15 η = 0. 6025 ∗ 100% η = 60 .25% 𝑊𝑚𝑎𝑥 = η ∗ 𝑄𝑖𝑛 𝑊𝑚𝑎𝑥 = 0. 6025 ∗ 1 083 333. 33 𝑊𝑚𝑎𝑥 = 652 758. 34 W η = 1 − 𝑇𝑠𝑢𝑚 𝑇𝑓𝑢𝑒𝑛𝑡𝑒 η = 1 −
277. 15
278. 15 η = 0. 5692 ∗ 100% η = 56 .92% 𝑊𝑚𝑎𝑥 = η ∗ 𝑄𝑖𝑛 𝑊𝑚𝑎𝑥 = 0. 5692 ∗ 1 083 333. 33 𝑊𝑚𝑎𝑥 = 616 654. 45 W

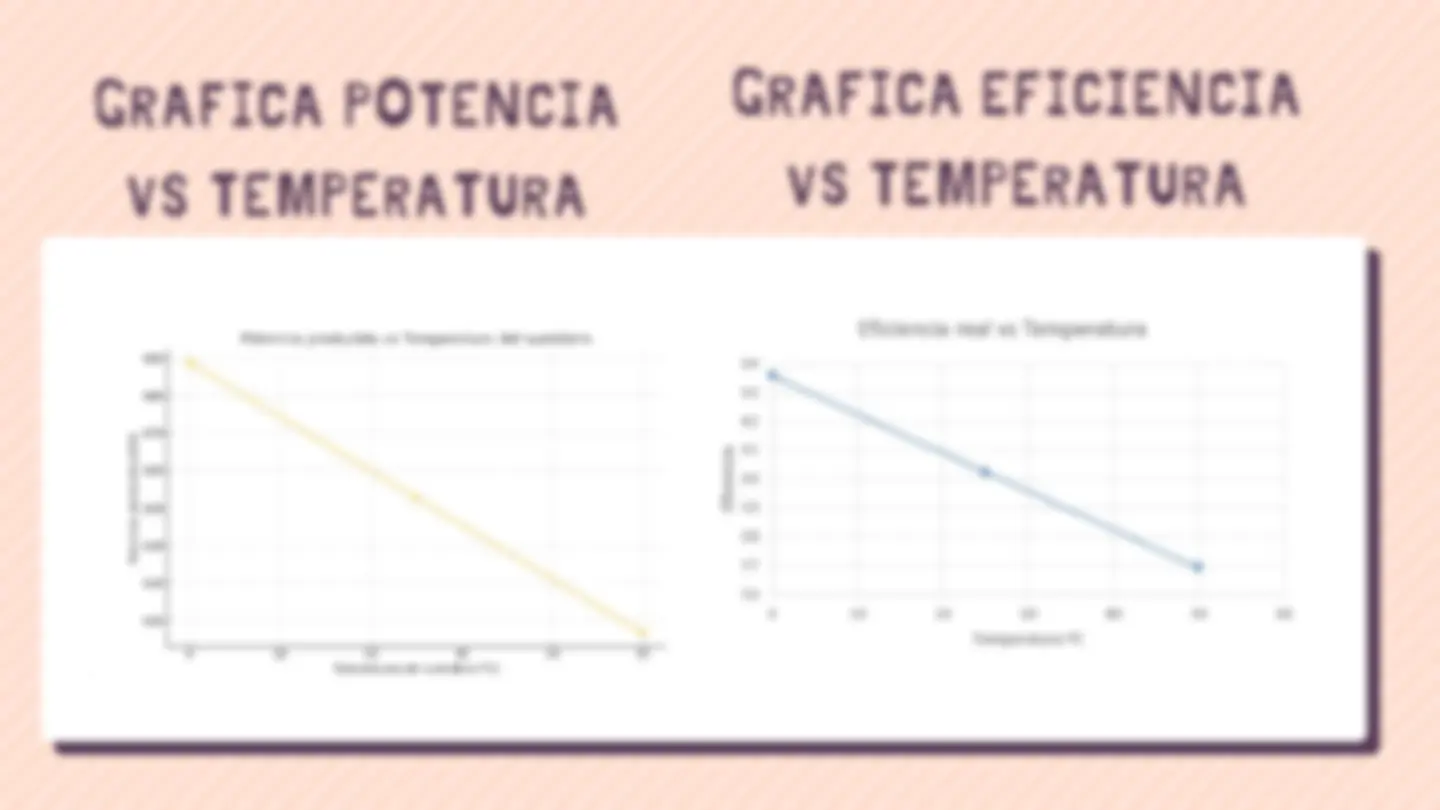
GRÁFICA 1: EFICIENCIA VS TEMPERATURA DE LA FUENTE

• A mayor temperatura de la fuente, aumenta la eficiencia térmica.
• Para un mismo sumidero, las curvas son crecientes, pero con rendimientos marginales decrecientes.
• La eficiencia es mayor cuando el sumidero es más frío (0 c), como se espera por la fórmula de carnot. GRÁFICA 2: POTENCIA VS TEMPERATURA DE LA FUENTE - La Potencia aumenta con la temperatura de la fuente. - Cuando el sumidero es más frío, se obtiene más potencia para la misma entrada de calor. - A bajas temperaturas de la fuente, la máquina entraga poca potencia (poca diferencia de temperaturas).

Una maquina térmica opera entre una fuente a 477 °C y un sumidero a 25 °C. Si se suministra calor a la maquina térmica a una tasa constante de 65000 KJ/min y se rechaza calor hacia un sumidero a razón de 27784 KJ/min, determine la producción de potencia en Watts y su eficiencia. Estudie los efectos de las temperaturas de la fuente de calor y del sumidero sobre la potencia y la eficiencia térmica del ciclo.

Por otro lado, el Caso 2 analiza el rendimiento de una máquina térmica basándose en el calor real rechazado al sumidero. Esto significa que los cálculos de potencia y eficiencia en el Caso 2 consideran las irreversibilidades inherentes a los procesos del mundo real, ya que la potencia se determina restando el calor de salida real del calor de entrada. En este ejemplo en específico, los valores de eficiencia y potencia obtenidos en el Caso 2 (por ejemplo, 60. 25 % de eficiencia y 652 , 766. 67 W de potencia para el sumidero a 25 °C) son muy cercanos a los del Caso 1. Esta cercanía sugiere que los valores de calor rechazado "reales" proporcionados para el Caso 2 están idealizados o representan un escenario en el que el motor se acerca mucho al rendimiento teórico.

La comparación resalta que, si bien el Caso 1 establece el máximo teórico de rendimiento que una máquina térmica puede alcanzar bajo condiciones ideales, el Caso 2 , al incorporar el calor rechazado real, se aproxima más a la realidad operativa. Las diferencias, aunque mínimas en este caso particular, generalmente se deben a irreversibilidades como la transferencia de calor a través de diferencias de temperatura finitas, la fricción, las caídas de presión del fluido y las pérdidas de calor al entorno. Estos factores son inherentes a cualquier máquina térmica real y siempre harán que su eficiencia y potencia sean menores que las de un ciclo de Carnot ideal.

Como conclusion puedo mencionar que la máquina térmica revela que la temperatura del sumidero tiene un efecto determinante sobre su rendimiento. A medida que esta temperatura aumenta, la capacidad del sistema para convertir calor en trabajo útil disminuye, reduciendo tanto la eficiencia como la potencia de salida. Al comparar los resultados con el ciclo ideal de Carnot, se observa que este siempre ofrece un rendimiento superior, aunque inalcanzable en la práctica debido a las irreversibilidades del sistema. Aun así, el modelo de Carnot es una herramienta útil para entender los límites teóricos del rendimiento térmico y guiar el diseño de tecnologías más eficientes. Para maximizar la eficiencia, es fundamental mantener una alta diferencia de temperatura entre la fuente caliente y el sumidero frío. Esto no solo mejora la conversión de energía en trabajo útil, sino que también promueve el desarrollo de sistemas más sostenibles. Además, el estudio destaca que incluso variaciones pequeñas en la temperatura del sumidero pueden afectar significativamente el rendimiento, lo que subraya la importancia de un control térmico preciso en el diseño de ciclos térmicos eficientes.

El análisis de la máquina térmica muestra que tanto la eficiencia como la potencia generada dependen fuertemente de las temperaturas de la Fuente caliente y del sumidero frío. Específicamente, se confirma que al aumentar la temperatura de la Fuente o disminuirá la del sumidero, la eficiencia del ciclo de Carnot mejora significativamente, lo cual se traduce directamente en una mayor producción de potencia útil. En el caso específico de operar entre 477 c y 25 c, se logra una eficiencia máxima teórica del 60.25% y una potencia de aproximadamente 652.76 kW, lo cual demuestra la alta capacidad de conversión energética bajo estas condiciones. Este estudio también evidencia que incluso pequeñas variaciones en la temperatura del sumidero pueden tener un impacto considerable en el rendimiento del sistema, por lo que controlar adecuadamente estas variables es clave en el diseño y la optimización de ciclos térmicos eficientes.