Manual de Cálculo: Guía para Estudiantes de Ingeniería y Ciencias, Study notes of Industrial management

Download Manual de Cálculo: Guía para Estudiantes de Ingeniería y Ciencias and more Study notes Industrial management in PDF only on Docsity!

Manual de Cálculo

Unidad de Acompañamiento y

Acceso a la Universidad

MANUAL DE CALCULO

UNIDAD D E ACOMPAÑAMIENTO Y ACCESO A L A U N I VERSIDAD 7

E

l objetivo de este instrumento es contribuir al desarrollo de los aprendizajes de estudiantes de primer año promoción 2018, pertenecientes a las carreras de Ingeniería civil, Ingeniería civil industrial, Ingeniería Civil Eléctrica, Ingeniería Civil Informática, Contador Auditor, Ingeniería comercial y Pedagogía en educación medía en matemáticas en los ramos de Álgebra, Cálculo e Introducción al Análisis, por ende se detalla con precisión cada procedimiento inmerso en la resolución de un problema y los contenidos que el educando debe saber para dar solución a las problemáticas planteadas.

INTRODUCCIÓN

Software de Apoyo

¿Has usado alguna vez una herramienta que te ayude a resolver tus ejercicios? En internet existe una gran cantidad de opciones y una de ellas es:

Escanéa el código QR para visitar el sitio web

¡Te invito a descubrir sus prestaciones! Y claro, a buscar otras opciones hasta que elijas la que más te acomode.

8 UNIDAD D E ACOMPAÑAMIENTO Y ACCESO A L A U N I VERSIDAD AD D E ACOMPAÑAMIENTO Y ACCESO A L A U N I VERSIDADUNID 9

Conjuntos numéricos

Los Números Naturales ℕ

Los Números Naturales son las primeras abstracciones que realiza el hombre al surgir los conceptos de "unidad" y de "cuenta". Los Números Naturales son un conjunto ordenado de infinitos elementos y que inicia con la unidad o 1. Cualquier otro elemento puede ser formado a partir de la adición sucesiva de unidades. Así, 2 = 1 + 1, 3 = 2 + 1 = 1 + 1 + 1, etc. En notación de conjunto, los Números Naturales se definen como: ℕ = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, .....} Cada número Natural posee un sucesor, y todos tienen un antecesor menos el primero, el 1. Dentro del conjunto de los números Naturales se pueden hallar importantes subconjuntos tales como, los numeros pares, los numeros impares, los numeros primos, lo numeros compuestos. Para un n particular tambien pueden definirse sus conjuntos de multiplos y divisores.

Los Números Cardinales ℕ 0

Luego del conocimiento de la existencia de los numeros Naturales, surge la necesidad de representar la ausencia o nulidad. Para esto se agrega el cero, generando así el conjunto de los Cardinales ℕ0 = ℕ ∪ {0}

Los Números Enteros ℤ

Ciertas situaciones de la naturaleza no pueden ser explicadas con las cantidades contenidas en el conjunto de los números Cardinales, como por ejemplo las temperaturas bajo cero, los pisos de un edificio bajo el nivel de la superficie, entre otros. En la antigüedad ya se vislumbró esta necesidad por ejmplo a partir de la sustraccion de cardinales. De esta manera, se agregan a los números Cardinales las cantidades negativas, formando asi el conjunto de los números Enteros. ℤ = { Números Negativos } U ℕo = {...–5, –4, –3, –2, –1, 0, 1, 2, 3, 4,... } Cumpliéndose la relación: ℕ ⊂ ℕo ⊂ ℤ

Los Números Racionales ℚ

Una fracción es una partición de “una cosa”. En matemática, las "cosas" que se parten o fraccionan son cantidades. Supongamos que el rectángulo de la figura representa una cantidad cualquiera que ha sido "fraccionada" o dividida en dos partes iguales. Cada parte de la división es una fracción del total y como el total se dividió en dos, cada fracción es una mitad del total, es decir, del todo.

Luego, el denominador de la fracción representa el total de partes y el numerador la cantidad de partes considerada en la cantidad.

Nota

La división por cero (denominador cero en una fracción) no existe debido a que no podemos considerar partes de un todo inexistente.

Al igual que los conjuntos anteriores, los números racionales son infinitos, no obstante esta infinidad de valores existe incluso entre cada valor que lo compone. Esto da origen a la propiedad de densidad del conjunto Q, lo que significa que siempre entre dos racionales cualesquiera, por muy próximos que estén, encontraremos un tercero al medio.

Asi, un número racional es todo número formado por el cuociente de dos números enteros cualesquiera, con la sola restricción que el denominador o divisor no sea el entero cero. Por extensión, este conjunto sería, aproximadamente

ℚ = {-∞ ; ... ;–2; ... ; ; ... ;–1; ... ; ; ... ;–0,5; ... ; 0 ; ... ; ; ... ; ; ... ;0,75; ... ; 1;....+∞}

Los Números Irracionales ℚ*

Existen números decimales infinitos que no son periódicos ni semiperiódicos. Un ejemplo familiar es el número π que por ejemplo se utiliza en el cálculo de áreas y perímetros de circunferencias. Este número π corresponde a la expresión 3,1415926..... que posee infinitas cifras decimales sin ningún período. Así como el número π existen infinitos números en el universo matemático que poseen la misma característica: tal es el caso de los números , etc. Al ser estos números infinitos no periódicos no es posible transformarlos en fracción, pues no existen dos números enteros cuyo cuociente sea igual a alguno de ellos y ello implica que no son números racionales. Dado que existen infinitos números con tales características, han sido agrupados en un solo conjunto denominado conjunto de los números irracionales el cual designamos por el símbolo ℚ. Podrás notar que si hacemos ℚ ⋂ ℚ, el conjunto intersección es vacío (φ).

Los Números Reales ℝ

Se define el conjunto de los números Reales como la unión de todos los números conocidos definido simbolicamente por: Los Números Reales = ℝ = ℚ ∪ ℚ* El conjunto de los números Reales es la base de estudio de la presente guía, es un conjunto ordenado, denso y de cardinalidad infinita. Sus elementos pueden ser representados en la recta Real.

12 UNIDAD D E ACOMPAÑAMIENTO Y ACCESO A L A U N I VERSIDAD AD D E ACOMPAÑAMIENTO Y ACCESO A L A U N I VERSIDADUNID 13

Ejemplo

Sea A=

Decidir si A es acotado superior y/o inferiormente

Las raíces serían: x 1 =-2 ; x 2 =-1,05 ; x 3 =1, Siendo la solución: A = ]-2,-1,05 [ ∪ ] 1,162, + ∞[ Por lo tanto A es acotado inferiormente pero no superiormente. En el análisis de supremo e ínfimo de A: inf(A)=-2 y sup(A)=no existe En el análisis de máximo y mínimo de A: min(A)=∄ y máx(A)=∄

Sea S⊂R 1.- Si S es acotado superiormente, diremos que uo es supremo de S si se cumple que uo es cota superior de S ᴧ uo ≤u para cualquier cota superior u. 2.- Si S es acotado inferiormente, diremos que vo es ínfimo de S si se cumple que vo es cota inferior de S ᴧ vo ≥v para cualquier cota inferior v.

Nota

uo =sup(S) vo =(S) Si el supremo pertenece a S, entonces se llamará máximo. De la misma forma, si el ínfimo pertenece a S, entonces se llamará mínimo. Una importante relación a tener en cuenta es Sea S⊂R, sup(S)=-{-x:x∈S}

Ejemplo

Demuestre que (ab)-1=a-1^ b - (ab)-1^ = (ab) -11 , por inverso multiplicativo (ab)-1^ = (ab) -1^ * (a * a-1^ ), por neutro multiplicativo (ab)-1^ = [(ab) -1^ * (aa-1^ )]1, por inverso multiplicativo (ab)-1^ = [(ab) -1^ (aa-1^ )](bb -1), por asociatividad (ab)-1^ = (ab) -1^ * [(bb -1)(aa-1^ )], por asociatividad (ab)-1^ = (ab) -1^ * [a(a-1b)b -1^ ], por conmutatividad (ab)-1^ = (ab) -1^ * [a(ba-1)b -1^ ], por asociatividad (ab)-1^ = (ab) -1^ * [(ab)(a-1*b -1)], por asociatividad (ab)-1^ = [(ab) -1^ (ab)](a-1b -1^ ), por inverso multiplicativo: x(-1)^ x= (ab)-1^ = 1(a-1^ * b -1^ ), por neutro multiplicativo (ab)-1^ = (a-1^ *b -1^ ) Por lo tanto, (ab)-1=a-1^ b -

Nota

Debes ir resolviendo el ejercicio enunciado, paso a paso, declarando la propiedad utilizada.

Intervalos reales

Los Números Reales los podemos representar en una recta, llamada Recta Real. Se elige un punto a la izquierda y el otro a la derecha y a cada punto le corresponde un Número Real. Por lo que si x<y , “x” estará a la izquierda de “y”. Así los números positivos estarán a la derecha del “0” y los negativos a la izquierda de este. Existe un conjunto de puntos que se van a encontrar entre “a” y “b” al que le denominaremos intervalo. Un intervalo es un conjunto infinito de números reales, veamos los diferentes tipos.

Intervalo cerrado

Intervalo abierto

Intervalo semi abierto

Intervalos no acotados

Pueden ser abiertos o semi abiertos en el extremo acotado

Te invitamos a ver:

14 UNIDAD D E ACOMPAÑAMIENTO Y ACCESO A L A U N I VERSIDAD AD D E ACOMPAÑAMIENTO Y ACCESO A L A U N I VERSIDADUNID 15

Ilustración 1 Supremos e Ínfimos para distintos tipos de intervalos

Nota

Todo subconjunto no vacío y acotado superiormente de R tiene supremo.

Ejemplo

1. Dibuje el intervalo que represente cada expresión
   2. Escriba la desigualdad que represente el intervalo dado

18 UNIDAD D E ACOMPAÑAMIENTO Y ACCESO A L A U N I VERSIDAD AD D E ACOMPAÑAMIENTO Y ACCESO A L A U N I VERSIDADUNID 19

Inecuaciones con denominador numérico

Son desigualdades que involucran términos fraccionarios cuyo denominador no contiene variables.

Ejemplo

2/3 (a+1)+1/5 (a-2)≽3/2 (a-2)+1/15(a-1) /MCM= 20(a+1)+6(a-2)≽45(a-2+2(a-1) / Se resuelven los productos 20a+20+6a-12≽45a-90+2a-2 /Se reducen términos semejantes 26a+8≽47a-92 /-47a -21a+8≽-92 /- -21a≽-100 /(-1) 21a≼100 /: a≼100/

Inecuaciones con producto de polinomios

Son desigualdades que al efectuar los productos se obtienen polinomios de grados mayores o iguales a dos, lo cual da lugar a un análisis mas acabado de los valores para los que la relación establecida en la desigualdad es cierta.

Ejemplo

Encuentre el conjunto solución de la inecuación x^2 -5x+4≤ Obtenemos las raíces de x^2 -5x+4=0.

x^2 -5x+4≤0 →(x-4)(x-1)≤

Luego estas raíces, que constituyen los valores de x que anulan la expresión definen intervalos relevantes de análisis del comportamiento de cada factor. Así establecemos tres zonas de análisis y estudiamos con la tabla francesa en cuales cada factor es positivo o negativo y en la última efectuamos la multiplicación de signos de cada columna.

(-∞,1] [1,4] [4,∞)

(x-1) - + +

(x-4) - - +

(x-1)(x-4) + - +

Sólo la zona 2 satisface la ecuación, es decir la solución final es x∈[1,4]

Inecuaciones con denominador variable

Son desigualdades que involucran términos fraccionarios cuyo denominador si contiene variables. Usualmente este tipo de inecuaciones da lugar a expresiones de mayor complejidad que deben ser analizadas por casos utilizando la tabla francesa.

Ejemplo

Determinamos los valores de x que anulan esta expresión (numerador y denominador) y obtenemos los valores críticos x = -1,1,2 con lo cual establecemos cuatro zonas de análisis y estudiamos con la tabla francesa

en cuales cada factor es positivo o negativo y en la última efectuamos la multiplicación de signos de cada columna.

20 UNIDAD D E ACOMPAÑAMIENTO Y ACCESO A L A U N I VERSIDAD AD D E ACOMPAÑAMIENTO Y ACCESO A L A U N I VERSIDADUNID 21

Asi, la solución es: x ∈ ] – ∞ , –1[ ∪ ]1, 2 [

Ejemplo

Luego esta expresión final será mayor o igual a cero en dos casos Si tanto numerador como denominador son positivos Si tanto numerador como denominador son negativos Analizamos para que valores de x el numerador y el denominador son positivos. x^2 +x+2≥0 ; (x+1)(x-1)≥ Solución para x^2 +x+2≥0: x^2 +x+2=0 No tiene soluciones. Además el valor del coeficiente a es positivo. O sea y=x^2 +x+2 nunca corta al eje x y siempre está por encima del eje x(solo tiene raíces complejas). Así que la inecuación se verifica para todos los valores de x, x∈(-∞,∞). Solución para (x+1)(x-1)>0: Determinamos los valores de x que anulan esta expresión y obtenemos x=-1 y x=1 con lo cual establecemos tres zonas de análisis y estudiamos con la tabla francesa en cuales cada factor es positivo o negativo y en la última efectuamos la multiplicación de signos de cada columna.

(x+1) - + +

(x-1) - - +

(x+1)(x-1) + - +

Entonces los intervalos que satisfacen la inecuación son x∈(-∞,-1)∪(1,∞) La solución sería x∈(-∞,∞)∪{x∈(-∞,-1)∪(1,∞)}→x∈(-∞,-1)∪(1,∞)

Cuando el numerador y el denominador son negativos. x^2 +x+2≤0 ; (x+1)(x-1)<

Entonces la solución es x ∈ (-∞,-1) ∪ (1,∞) La inecuación x^2 +x+2≤0 no se satisface nunca, no teniendo solución en los reales. Como en esta ecuación no posee solución y sabiendo que la solución del sistema es la intersección de las soluciones correspondientes, podemos afirmar que el intervalo solución es vacío.

EJERCICIOS PROPUESTOS

Resolver x^2 +5x + 6 > 0

24 UNIDAD D E ACOMPAÑAMIENTO Y ACCESO A L A U N I VERSIDAD AD D E ACOMPAÑAMIENTO Y ACCESO A L A U N I VERSIDADUNID 25

Plano Real

ℝ^2 es un conjunto de pares ordenados compuesto por números reales. (a,b)≠(b,a) (a,b)=(b,a)↔a=b

Eje de Coordenadas

Primer cuadrante: I = {(X,Y) ∈ ℝ 2 : x>0˄y > 0} Segundo cuadrante: II = {(X,Y) ∈ ℝ 2 : x<0˄y > 0} Tercer cuadrante: III = {(X,Y) ∈ ℝ 2 : x<0˄y < 0} Cuarto cuadrante: IV = {(X,Y) ∈ ℝ 2 : x>0˄y < 0}

Distancia entre dos puntos

Dado los puntos P(x 1 ,y 1 ) y Q(x 2 ,y 2 ) del plano, La distancia entre A y B está dada por d (P,Q)=√((x 2 -x 1 )^2 +(y 2 -y 1 )^2 )

Punto Medio

Dado los puntos P(x 1 ,y 1 ) y Q(x 2 ,y 2 ) del plano. El punto medio entre P y Q es el punto M que se encuentra en el segmento que une P y Q además equidista de ambos extremos.

d (M,P) = d(M,Q) ˄ M ∈ (PQ) Y las coordenadas están dadas por:

División de un segmento en una razón

Dado los puntos P(x 1 ,y 1 ) y Q(x 2 ,y 2 ) del plano. El punto R que divide el segmento (PQ) en una razón r> está dado por

Lugar Geométrico

Un Lugar geométrico en ℝ^2 es un conjunto de puntos del plano que verifican una o más condiciones geométricas y/o algebraicas. En general, podemos escribirlos como conjunto R={ (x,y) ∈ ℝ 2 : F(x,y) = 0 }

El lugar geométrico de una ecuación es una curva que contiene aquellos puntos y sólo aquellos puntos cuyas coordenadas satisfacen la ecuación.

Recta

Lugar geométrico de los puntos del plano tales que si tomamos dos de ellos, la razón entre la diferencia en la segunda coordenada respecto a la diferencia en la primera coordenada se mantiene constante. Razón que se llama pendiente. m es la pendiente y P(x 0 ,y 0 ) y Q(x,y) ∈ recta L

Nota

Si conocemos dos puntos podemos determinar la pendiente de la recta.

Si conocemos la pendiente de la recta, podemos conocer el ángulo formado por el eje x y la recta. m=tanα

Forma Principal

L: y=mx+b

m es la pendiente y b el coeficiente de posición (intersección de la recta con el eje y)

Forma General

L: Ax+By+C=

Distancia Punto-Recta

Considerar L: Ax+By+C=0 y un punto en el plano P(x 0 ,y 0 ). La distancia está dada por:

26 UNIDAD D E ACOMPAÑAMIENTO Y ACCESO A L A U N I VERSIDAD AD D E ACOMPAÑAMIENTO Y ACCESO A L A U N I VERSIDADUNID 27

Ejemplos

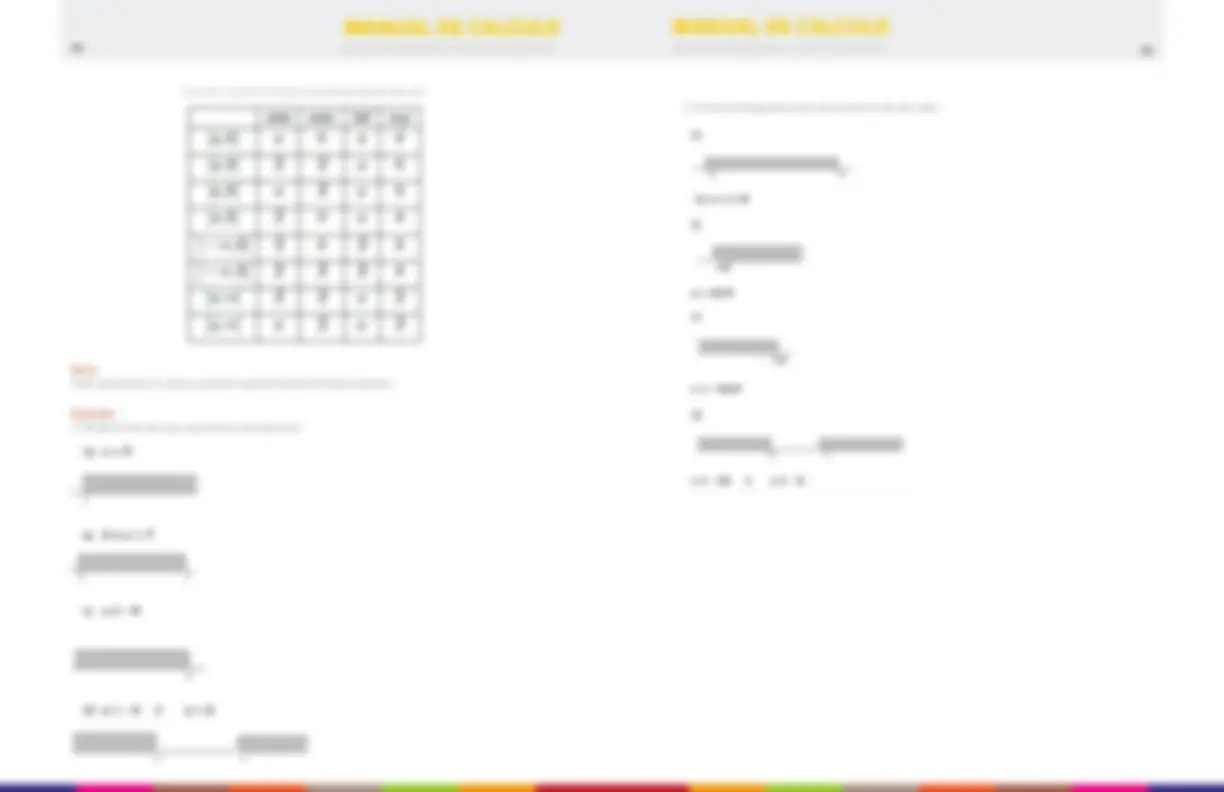
Calcular la distancia entre los puntos A (2,5) y B(-4,-3)

d (A,B) = √((-4-2)^2 +(-3-5)^2 ) =√(36+64) =√ =

Los vértices de un cuadrilátero son A (4,5), B(-2,4), C(-3,-2), D(2,-3), calcule su perimetro P=d(A,B)+d(B,C)+d(C,D)+d(D,A)

Calculemos por separado las distancias: d(A,B)=√((-2-4)^2 +(4-5)^2 )=√

d(B,C)=√((-3+2)^2 +(-2-4)^2 )=√

d(C,D)=√((2+3)^2 +(-3+2)^2 )=√

d(D,A)=√((4-2)^2 +(5+3)^2 )=√

Luego calculamos P sumando las distancias calculadas P=√37+√37+√37+√ P=2√37+√26+2√

Circunferencia

Lugar geométrico de puntos P del plano que equidistan de un punto conocido C, llamado centro. La distancia del centro a cualquier punto de la circunferencia la llamaremos radio (r). C = { (x,y) ∈ R 2 : d(P,C) = r }

Ecuación Principal: d(P,C) = r ↔ √((x-h)^2 + (y-k)^2 ) = r

Ecuación General: x^2 +y^2 +Cx+Dy+E=

Ejemplo

Determinar la ecuación de una circunferencia que pasa por el punto P (1,0), sabiendo que es concéntrica a la representada por la ecuación: x^2 +y^2 -2x-8y+13= Completando los trinomios cuadrados perfectos: (x^2 -2x+1-1)+(y^2 -8y+16-16)+13= (x-1)^2 +(y-4)^2 = De la expresión anterior encontramos que el centro es C (1,4), es decir h=1 y k=4. Como a 2 =4, entonces a=2. El radio a de la circunferencia buscada, se calcula como la distancia del punto P al centro C. a=(PC)= √((1-1)^2 + (0-4)^2 ) = 4 Por lo tanto a 2 =16. Sustituyendo este valor y los de h y k en la fórmula (x-h)^2 +(y-k)^2 =a^2 , encontramos: (x-1)^2 +(y-4)^2 =

Parábola

Lugar geométrico de puntos del plano P que equidistan de un punto conocido F (foco) y de una recta llamada directriz (D). P={(x,y)∈ R^2 :d(P,F)=d(P,D)} Ecuación Principal vertical: (x-h)^2 =4p(y-k) Ecuación General vertical: x^2 +Cx+Dy+E= Ecuación Principal horizontal: (y-k)^2 =4p (x-h)

30 UNIDAD D E ACOMPAÑAMIENTO Y ACCESO A L A U N I VERSIDAD AD D E ACOMPAÑAMIENTO Y ACCESO A L A U N I VERSIDADUNID 31

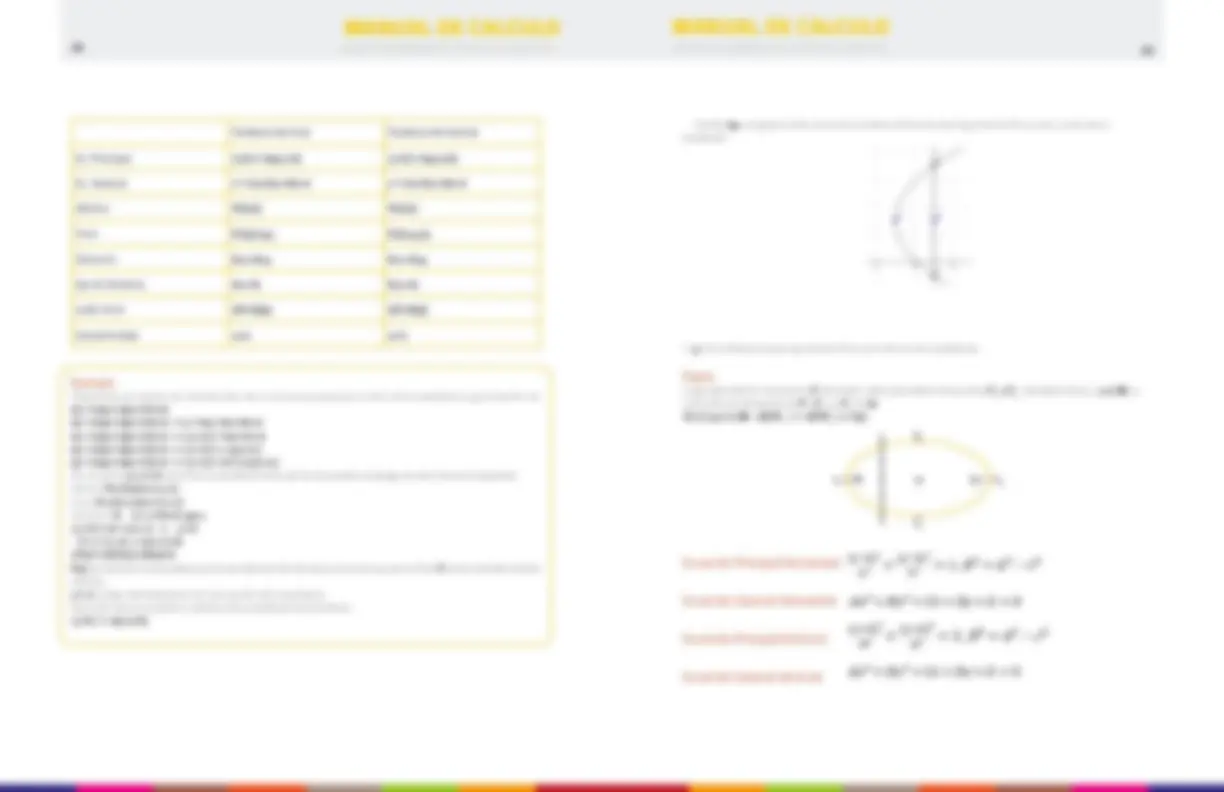
Elipse Horizontal Elipse Vertical

Ec. Principal

Ec. General Ax 2 + By^2 + Cx + Dy + E = 0

Centro C(h,k)

Focos F 1 (h-c,k),F 2 (h+c,k) F 1 (h,k-c),F 2 (h,k+c)

Vértices (Eje mayor)

Vértices (Eje menor)

V 1 (h-a,k),V 2 (h+a,k)

V 3 (h,k-b),V 4 (h,k+b)

V 1 (h,k-a),V 2 (h,k+a)

V 3 (h-b,k),V 4 (h+b,k)

Excentricidad

Resumen Elipse:

Nota

El valor de a indicará la forma de la elipse. Eje Focal: Segmento que une los focos. Su longitud es 2c. Eje Mayor: Segmento que contiene a los focos y sus extremos son puntos de la elipse. Su longitud es 2ª. Eje Menor: Segmento perpendicular al eje mayor, sus extremos son puntos de la elipse y su punto medio coincide con el del eje mayor. Su longitud es 2b. Centro: Punto intersección entre el eje mayor y el menor. Vértices: Son los puntos extremos de los ejes mayor y menor

Ejemplo

Se construye una plataforma de skate con forma de arco semi elíptico de 20 mts lineales de largo y una profundidad de 4mts. Para su construcción se consideran 4 pilares, 2 en los extremos y dos postes interiores ubicados a tres metros de éstos. Determinar la altura de los postes interiores: Para calcular la altura es necesario ubicar la plataforma en un sistema de ejes coordenados. El eje mayor tiene longitud 20 por lo tanto 2a=20→a= La profundidad es 4 , por lo tanto b=4 teniendo como centro (0,4) Reemplazando los valores se tiene

Para determinar la altura de los postes interiores, basta con evaluar x=7 en la ecuación

Se concluye que la altura de los postes es de 1,14 mts, ya que la plataforma corresponde a la semi elipse inferior. El eje mayor es horizontal por lo tanto la ecuación de la elipse que se considera es:

Hipérbola

Lugar geométrico de puntos P del plano, tales que dados dos puntos F 1 y F 2 , llamados focos, y a ∈ ℝ+, el valor absoluto de la diferencia de las distancias de P a F 1 y a F 2 es 2a. E = { (x,y) ∈ ℝ 2 : | d(P,F 1 )-d(P,F 2 )|=2a}

32 UNIDAD D E ACOMPAÑAMIENTO Y ACCESO A L A U N I VERSIDAD AD D E ACOMPAÑAMIENTO Y ACCESO A L A U N I VERSIDADUNID 33

Ecuación Principal Horizontal:

Ecuación General Horizontal: Ax^2 +By^2 +Cx+Dy+E=

Ecuación Principal Vertical:

Ecuación General Vertical:

Elementos de una Hipérbola

Eje Focal: Segmento que une los focos. Su longitud es 2c. Vértices: Son los puntos de intersección del eje focal y la hipérbola. Centro: Punto medio eje focal. Eje Transverso: Segmento que une los vértices. Su longitud es 2a. Eje Conjugado: Segmento perpendicular al eje focal, cuyo punto medio es el centro. Su longitud.

La ecuación debe tener la forma dada por la fórmula (x-h)^2 +(y-k)^2 =a^2 debiendo ser las coordenadas h y k del centro, las mismas que la de la circunferencia dada y las calculamos llevando a la forma común, la ecuación de la circunferencia conocida. Resumen hipérbola:

Hipérbola Horizontal Hipérbola Vertical

Ec. Principal

Ec. General Ax^2 +By^2 +Cx+Dy+E=

Centro C(h,k)

Focos F 1 (h-c,k),F 2 (h+c,k) F 1 (h,k-c),F 2 (h,k+c)

Vértices V 1 (h-a,k),V 2 (h+a,k) V 1 (h,k-a),V 2 (h,k+a)

Excentricidad

Asíntotas

Ejemplo

Encuentre la ecuación de la hipérbola vertical con centro en (2,-1) cuya distancia entre los vértices es 12 y su excentricidad es 3. Solución:

Sea C=(2,-1) centro de la hipérbola vertical y cuya distancia entre los vértices es 12 y su excentricidad

luego los vértices son V 1 =(2,5)y V 2 =(2,-7),pues d(V 1 ,V 2 )=

Entonces y c 2 =a^2 +b^2 ↔b^2 =c^2 -a^2

Por lo tanto

EJERCICIOS PROPUESTOS

1. Determine la distancia que existe entre las rectas: L1: y = 2x – 3 L2: y = 2x + 5
2. Los vértices de un triángulo son A(-1, 2), B(3, 5), C(1, 7) Determine y grafique: a) Ecuación de sus lados en forma principal y general b) Perímetro del triángulo ABC c) Ecuación de las transversales de gravedad d) Ecuación de las alturas e) Ecuación de las medianas f) Área de triángulo ABC
3. Hallar la ecuación de la circunferencia con centro en C(3, -2) y que es tangente al eje x.
4. Una circunferencia pasa por los puntos (-3, 3) y (1, 4), y su centro está sobre la recta 3x – 2y – 23 = 0. Hallar su ecuación.
5. Hallar el vértice, foco, directriz, longitud del lado recto y gráfica de: y^2 +16x= 2y-3x^2 = 5x^2 +4y=
6. Determine en cada caso centro, vértices, ejes mayor y menor, excentricidad y gráfica de la elipse. 25x^2 +9y^2 +100x-54y-44= 4x^2 +9y^2 -8x+36y+4=
7. Obtener la ecuación de la hipérbola si un vértice está en (0, 4) y un foco en (0, 5).
8. ¿Cuántas hipérbolas tienen su centro en (0, 0) y su foco en (1, 0)? Determine sus ecuaciones.

Ax^2 +By^2 +Cx+Dy+E=

Te invitamos a ver:

36 UNIDAD D E ACOMPAÑAMIENTO Y ACCESO A L A U N I VERSIDAD AD D E ACOMPAÑAMIENTO Y ACCESO A L A U N I VERSIDADUNID 37

Otros límites importantes

1.- lim =

2.- lim =

Álgebra de límites

Sean f y g funciones, tales que:

limf(x)=L 1 y limg(x)=L 2

Entonces:

1.- lim (f(x)+g(x))=L 1 +L (^2)

2.- lim (a(x))=a

3.- lim (f(x)*g(x))=L 1 *L 2

4.- lim

Teorema del sándwich:

Sean f y g y h funciones tales que f(x) ≤ g(x) ≤ h(x) para x ∈ v(x 0 ), salvo tal vez en x 0 entonces:

Si lim f(x)= lim h(x)= L se tiene lim g(x)=L

Teorema de composición:

Sean f y g dos funciones. Si para x∈v(x 0 ), salvo tal vez en x 0 entonces:

lim f(x)=l y lim g(x)= L entonces lim (g o f)(x)=L

Ejemplos

3x-1=3(2)-1=

-x^2 +x-2=-(1)^2 +1-2=-

4. Para levantar la indeterminación debemos factorizar
   5. Determine, si es posible, el valor de los siguientes límites:

38 UNIDAD D E ACOMPAÑAMIENTO Y ACCESO A L A U N I VERSIDAD AD D E ACOMPAÑAMIENTO Y ACCESO A L A U N I VERSIDADUNID 39

Límites laterales

Hay casos donde la función tiene distintas expresiones en el punto de interés, tanto a la izquierda como derecha, entonces se hace necesario analizar el límite en ambos sentidos. Sean f:A⊆R→R y x 0 ∈ R Sean v+^ (x 0 )=v(x 0 ) ∩ (x 0 ,+∞) y v-^ (x 0 )=v(x 0 )∩(-∞,x 0 ) Llamaremos “limite lateral por la derecha de la función f en x 0 ” a: limf(x)=L Si y sólo si (∀ϵ>0),(∃δ>0) ∶ (x∈v+^ (x 0 )) → (f(x) ∈ v (L) ) Es decir (∀ϵ>0),(∃δ>0) ∶ 0<x-x 0 <δ→|f(x)-L|<ϵ Llamaremos “limite lateral por la izquierda de la función f en x 0 ” a: lim f(x)=L

Si y sólo si (∀ϵ>0),(∃δ>0) ∶ (x∈v+^ (x 0 ))→(f(x)∈v(L)) Es decir (∀ϵ>0),(∃δ>0) ∶ 0<x 0 -x<δ→| f(x)-L|<ϵ El límite existe y es L si y sólo si ambos límites laterales existen y son iguales a L.

Ejemplo

Dada la siguiente función determine si existe el límite cuando x tiende a 2

Por lo cual el límite no existe.

Ejemplo

Dada la siguiente función determine si existe el límite cuando x tiende a -

Por tanto,el límite existe y es igual a-

Ejemplo

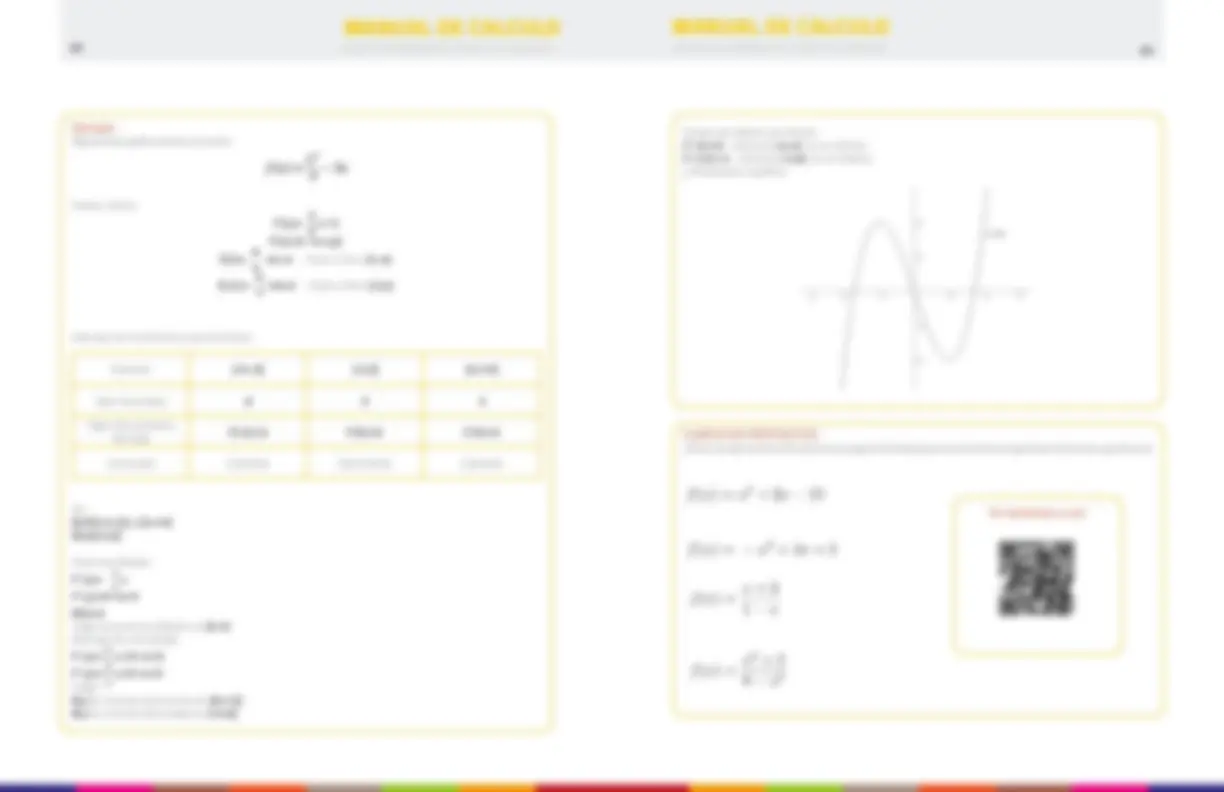
Determina para que valores de a y b es continua la función:

Si x≠0 y x≠2, la función es continua por ser trozos de parábolas y rectas. Si calculamos los límites laterales en x=0 y en x=2.

Si queremos que en x=0 sea continua, entonces -b=b→b=

Si queremos que en x=2 sea continua, entonces 2a+b=4b y como b=0, debe ser a=

La función es: