Machine Learning for Macrofinance, Summaries of Machine Learning

Download Machine Learning for Macrofinance and more Summaries Machine Learning in PDF only on Docsity!

Machine Learning for Macrofinance

Jes´us Fern´andez-Villaverde^1 August 8, 2022 (^1) University of Pennsylvania

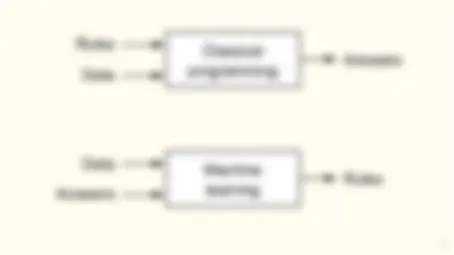
What is machine learning?

• Wide set of algorithms to detect and learn from patterns in the data (observed or simulated) and use them for decision making or to forecast future realizations of random variables.
• Focus on recursive processing of information to improve performance over time.
• In fact, this is clearer to see in its name in other languages: Apprentissage automatique or aprendizaje autom´atico.
• Even in English: Statistical learning.
• More formally: we use rich datasets to select appropriate functions in a dense functional space.

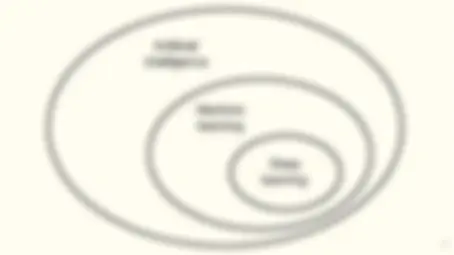
Artificial

intelligence

Machine learning

Deep learning

Figu

mac 4

The many uses of machine learning in macrofinance

• Recent boom in economics:
  1. New solution methods for economic models: my own work on deep learning.
  2. Alternative to older bounded rationality models: reinforcement learning.
  3. Data processing: Blumenstock et al. (2017).
  4. Alternative empirical models: deep IVs by Hartford et al. (2017) and text analysis.
• However, important to distinguish signal from noise.
• Machine learning is a catch-all name for a large family of methods.
• Some of them are old-fashioned methods in statistics and econometrics presented under alternative names.

A formal approach

The problem

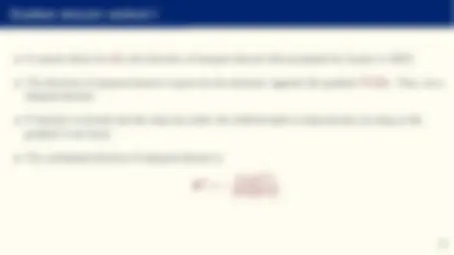
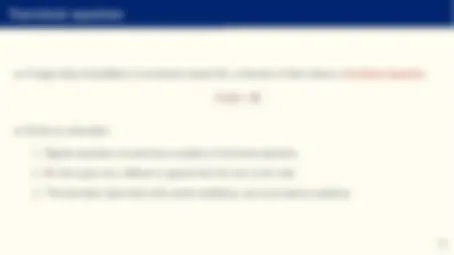
• Let us suppose we want to approximate (“learn”) an unknown function:

y = f (x)

where y is a scalar and x = {x 0 = 1, x 1 , x 2 , ..., xN } a vector (why a constant?).

• We care about the case when N is large (possibly in the thousands!).
• Easy to extend to the case where y is a vector (e.g., a probability distribution), but notation becomes cumbersome.
• In economics, f (x) can be a value function, a policy function, a pricing kernel, a conditional expectation, a classifier, ...

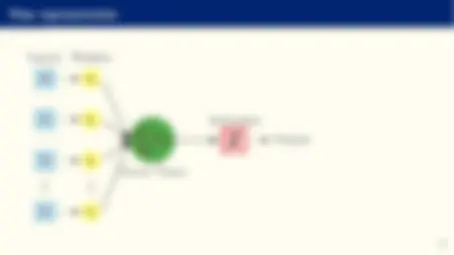
Flow representation

Inputs Weights

x 0 θ 0

x 1 θ 1

x 2 θ 2

xn θn

X^ n

i=

θi xi

Linear Trans.

Activation

Output

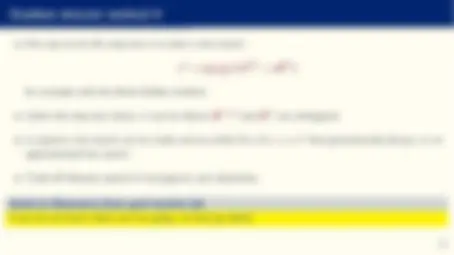
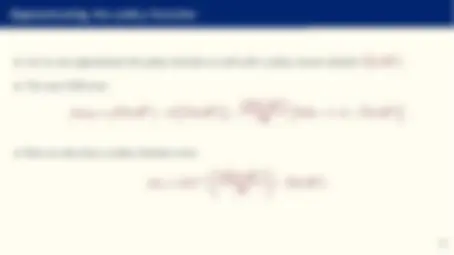
Comparison with other approximations

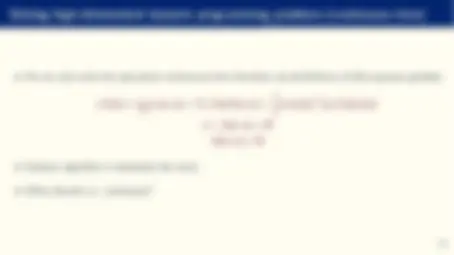
• Compare: y ∼= g NN^ (x; θ) = θ 0 +

X^ M

m=

θmϕ

X^ N

n=

θn,mxn

with a standard projection:

y ∼= g CP^ (x; θ) = θ 0 +

X^ M

m=

θmϕm (x)

where ϕm is, for example, a Chebyshev polynomial.

• We exchange the rich parameterization of coefficients for the parsimony of basis functions.
• In a few slides, I will explain why this is often a good idea. Suffice it to say now that evaluating a neural network is straightforward.
• How we determine the coefficients is also different, but this is less important.

x 0

x 1

x 2

Input Values

Input Layer

Hidden Layer 1

Hidden Layer 2

Output Layer

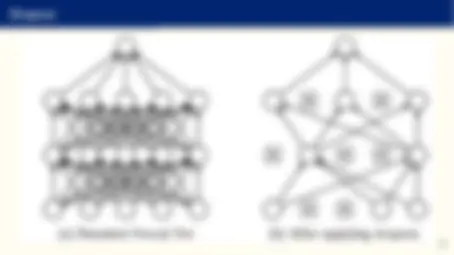
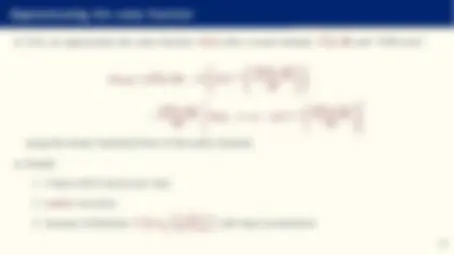
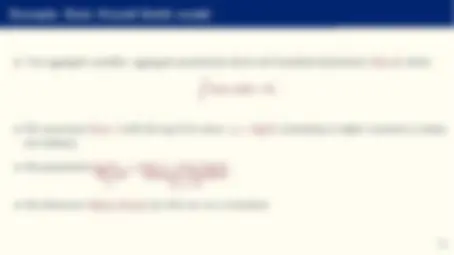
Deep learning II

• J is known as the depth of the network (deep vs. shallow networks). The case J = 1 is the neural network we saw before.
• From now on, we will refer to neural networks as including both single and multilayer networks.
• As before, we select θ such that g DL^ (x; θ) approximates a target function f (x) as closely as possible under some relevant metric.
• We can also add multidimensional outputs.
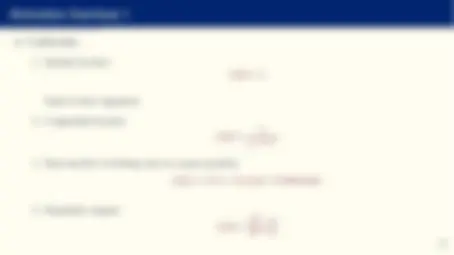
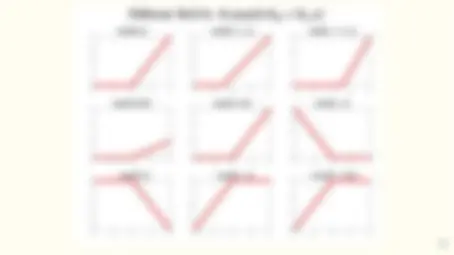
• Or even to produce a probability distribution as output, for example, using a softmax layer:

ym = ez J m− 1 PM m=1 ez

J m− 1

• All other aspects (selecting ϕ(·), J, M, ...) are known as the network architecture. We will discuss extensively at the of this slide block how to determine them.

tool for uncrumpling paper balls, that is, for disentang

A deep learning model is basically a very high-dime

Why do deep neural networks “work” better?

• Why do we want to introduce hidden layers?
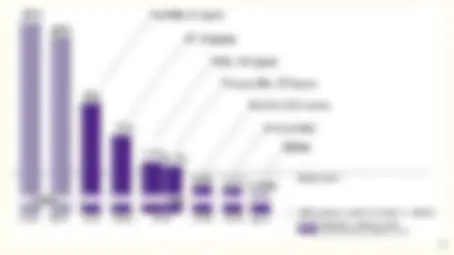
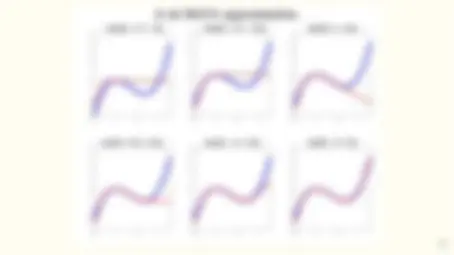
  1. It works! Evolution of ImageNet winners.
  2. The number of representations increases exponentially with the number of hidden layers while computational cost grows linearly.
  3. Intuition: hidden layers induce highly nonlinear behavior in the joint creation of representations without the need to have domain knowledge (used, in other algorithms, in some form of greedy pre-processing).