




























Study with the several resources on Docsity

Earn points by helping other students or get them with a premium plan


Prepare for your exams
Study with the several resources on Docsity

Earn points to download
Earn points by helping other students or get them with a premium plan
Community
Ask the community for help and clear up your study doubts
Discover the best universities in your country according to Docsity users
Free resources
Download our free guides on studying techniques, anxiety management strategies, and thesis advice from Docsity tutors
Lie group actions, surveying a variety of applications, including geometry, differential equations, computer vision, numerical analysis, the calculus of variations, and invariant flows.
Typology: Summaries
1 / 35

This page cannot be seen from the preview
Don't miss anything!




























Peter J. Olver† School of Mathematics University of Minnesota Minneapolis, MN 55455
Abstract. This article presents the equivariant method of moving frames for finite- dimensional Lie group actions, surveying a variety of applications, including geometry, differential equations, computer vision, numerical analysis, the calculus of variations, and invariant flows.
According to Akivis, [ 1 ], the method of moving frames originates in work of the Esto- nian mathematician Martin Bartels (1769–1836), a teacher of both Gauss and Lobachevsky. The field is most closely associated with Elie Cartan, [´ 21 ], who forged earlier contributions by Darboux, Frenet, Serret, and Cotton into a powerful tool for analyzing the geometric properties of submanifolds and their invariants under the action of transformation groups. In the 1970’s, several researchers, cf. [ 24 , 36 , 37 , 48 ], began the process of developing a firm theoretical foundation for the method. The final crucial step, [ 31 ], is to define a moving frame simply as an equivariant map from the manifold back to the transformation group. All classical moving frames can be reinterpreted in this manner. Moreover, the equivariant approach is completely algorithmic, and applies to very general group actions. Cartan’s normalization construction of a moving frame can be interpreted as the choice of a cross-section to the group orbits. This enables one to algorithmically construct an equivariant moving frame along with a complete systems of invariants through the induced invariantization process. The existence of an equivariant moving frame requires freeness of the underlying group action, i.e., the isotropy subgroup of any single point is trivial.
† (^) Supported in part by NSF Grant DMS 11–08894.
Classically, non-free actions are made free by prolonging to jet space, leading to differential invariants and the solution to equivalence and symmetry problems via the differential in- variant signature. Alternatively, applying the moving frame method to Cartesian product actions leads to the classification of joint invariants and joint differential invariants, [ 77 ]. Finally, an amalgamation of jet and Cartesian product actions dubbed multi-space was pro- posed in [ 78 ] to serve as the basis for the geometric analysis of numerical approximations, and systematic construction of invariant numerical algorithms, [ 54 ].
With the basic moving frame machinery in hand, a plethora of new, unexpected, and significant applications soon appeared. In [ 75 , 7 , 55 , 56 ], the theory was applied to produce new algorithms for solving the basic symmetry and equivalence problems of poly- nomials that form the foundation of classical invariant theory. In [ 20 , 10 , 2 , 6 , 91 , 72 ], the characterization of submanifolds via their differential invariant signatures was applied to the problem of object recognition and symmetry detection, [ 16 , 17 , 30 , 87 ]. Appli- cations to the classification of joint invariants and joint differential invariants appear in [ 31 , 77 , 11 ]. In computer vision, joint differential invariants have been proposed as noise- resistant alternatives to the standard differential invariant signatures, [ 28 , 69 ]. The ap- proximation of higher order differential invariants by joint differential invariants and, gen- erally, ordinary joint invariants leads to fully invariant finite difference numerical schemes, [ 19 , 20 , 10 , 78 , 54 ]. The all-important recurrence formulae lead to a complete charac- terization of the differential invariant algebra of group actions, and lead to new results on minimal generating invariants, even in very classical geometries, [ 79 , 43 , 81 , 47 , 44 ]. The general problem from the calculus of variations of directly constructing the invariant Euler-Lagrange equations from their invariant Lagrangians was solved in [ 57 ]. Applica- tions to the evolution of differential invariants under invariant submanifold flows, leading to integrable soliton equations and signature evolution in computer vision, can be found in [ 80 , 50 ].
Applications of equivariant moving frames that are being developed by other research groups include the computation of symmetry groups and classification of partial differ- ential equations [ 60 , 70 ]; geometry of curves and surfaces in homogeneous spaces, with applications to integrable systems, [ 61 , 62 , 63 ]; symmetry and equivalence of polygons and point configurations, [ 12 , 49 ], recognition of DNA supercoils, [ 90 ], recovering struc- ture of three-dimensional objects from motion, [ 6 ], classification of projective curves in visual recognition, [ 41 ]; construction of integral invariant signatures for object recognition in 2D and 3D images, [ 32 ]; determination of invariants and covariants of Killing tensors, with applications to general relativity, separation of variables, and Hamiltonian systems, [ 27 , 67 , 66 ]; further developments in classical invariant theory, [ 7 , 55 , 56 ]; computation of Casimir invariants of Lie algebras and the classification of subalgebras, with applica- tions in quantum mechanics, [ 13 , 14 ]. A rigorous, algebraically-based reformulation of the method, suitable for symbolic computations, has been proposed by Hubert and Kogan, [ 45 , 46 ].
Finally, in recent work with Pohjanpelto, [ 83 , 84 , 85 ], the theory and algorithms have recently been extended to the vastly more complicated case of infinite-dimensional Lie pseudo-groups. Applications to infinite-dimensional symmetry groups of partial differential equations can be found in [ 22 , 23 , 71 , 94 ], and to the classification of Laplace invariants
Definition 2.4. The invariantization of a function F : M → R is the unique invariant function I = ι(F ) that agrees with F on the cross-section: I | K = F | K.
In practice, the invariantization of a function F (z) is obtained by first transforming it according to the group, F (g · z) and then replacing the group parameters by their moving frame formulae g = ρ(z), so that ι[ F (z) ] = F (ρ(z) · z). In particular, invariantization of the coordinate functions yields the fundamental invariants: Iν (z) = ι(zν ). Once these have been computed, the invariantization of a general function F (z) is simply given by
ι
F (z 1 ,... , zn)
= F (I 1 (z),... , Ir(z)). (2.4)
In particular, the functions defining the cross-section (2.2) have constant invariantization, ι(Zν ) = cν , and are known as the phantom invariants. Thus, there are precisely m − r functionally independent fundamental invariants. Moreover, if I(z) is any invariant, then clearly ι(I) = I, which implies the elegant and powerful Replacement Rule
I(z 1 ,... , zn) = I(I 1 (z),... , In(z)), (2.5)
that can be used to immediately rewrite I(z) in terms of the fundamental invariants. Of course, most interesting group actions are not free, and therefore do not admit moving frames in the sense of Definition 2.1. There are two well-known methods that con- vert a non-free (but effective) action into a free action. The first is to look at the Cartesian product action of G on several copies of M , which leads to joint invariants. The second is to prolong the group action to jet space, which is the natural setting for the traditional moving frame theory, leading to differential invariants. Combining the two methods of jet prolongation and Cartesian product results in joint differential invariants. In applications of symmetry constructions to numerical approximations of derivatives and differential in- variants, one requires a unification of these different actions into a common framework, called multispace, [ 54 , 78 ]. These are discussed in turn in the following sections.
Traditional moving frames are obtained by prolonging the group action to the nth order submanifold jet bundle Jn^ = Jn(M, p), which is defined as the set of equivalence classes of p-dimensional submanifolds S ⊂ M under the equivalence relation of nth^ order contact at a single point; see [ 73 ; Chapter 3] for details. Since G preserves the contact equivalence relation, it induces an action on the jet space Jn, known as its nth^ order prolongation and denoted by G(n). The formulas for the prolonged group action are found by implicit differentiation. We can assume, without significant loss of generality, that G acts effectively on open subsets of M , meaning that the only group element that fixes every point in any open U ⊂ M is the identity element. This implies, [ 76 ], that the prolonged action is locally free on a dense open subset Vn^ ⊂ Jn^ for n ≫ 0 sufficiently large. In all known examples, the prolonged action is, in fact, free on such a Vn^ although there is, frustratingly, no general proof of this property. The points z(n)^ ∈ Vn^ are known as regular jets. The normalization construction based on a choice of local cross-section Kn^ ⊂ Vn^ to the prolonged group orbits can be used to produce a (locally defined) nth^ order equivariant
moving frame ρ(n): Jn^ → G in a neighborhood of any regular jet. Once the moving frame is established, the induced invariantization process will map general differential functions F (x, u(n)) to differential invariants I = ι(F ). The fundamental differential invariants are obtained by invariantization of the coordinate functions:
Hi^ = ι(xi), IJα = ι(uαJ ), α = 1,... , q, #J ≥ 0. (3.1)
These naturally split into two classes: The r = dim G combinations defining the cross- section will be constant, and are known as the phantom differential invariants. The re- mainder, called the basic differential invariants, form a complete system of functionally independent differential invariants. Indeed, if I(x, u(n)) = I(... xi^... uαJ.. .) is any dif- ferential invariant, then the Replacement Rule (2.5) allows one to immediately rewrite I = I(... Hi^... IJα.. .) in terms of the fundamental differential invariants. The moving frame also produces p independent invariant differential operators by invariantizing the usual total derivative operators, D 1 = ι(D 1 ),... , Dp = ι(Dp), which can be iteratively applied to lower order differential invariants to generate the higher order differential in- variants; see below for full details.
Example 3.1. The paradigmatic example is the action of the orientation-preserving Euclidean group SE(2) on plane curves C ⊂ M = R^2. The group transformation g ∈ SE(2) maps the point z = (x, u) to the point w = (y, v) = g · z, given by
y = x cos φ − u sin φ + a, v = x sin φ + u cos φ + b, (3.2)
where g = (φ, a, b) ∈ SE(2) are the group parameters. The prolonged group transforma- tions are obtained by successively applying the implicit differentiation operator
Dy = (cos φ − ux sin φ)−^1 Dx (3.3)
to v, producing
vy =
sin φ + ux cos φ cos φ − ux sin φ
, vyy =
uxx (cos φ − ux sin φ)^3
Observe that the prolonged action is locally free on the first order jet space J^1. (To simplify the exposition, we gloss over the remaining discrete ambiguity caused by a 180◦^ rotation; see [ 77 ] for a more precise development.) The classical moving frame is based on the cross-section K^1 = { x = u = ux = 0 }. (3.5)
Solving the corresponding normalization equations y = v = vy = 0 for the group parame- ters produces the right moving frame
φ = − tan−^1 ux , a = −
x + uux √ 1 + u^2 x
, b =
xux − u √ 1 + u^2 x
The classical left-equivariant Frenet frame, [ 39 ], is obtained by inverting the Euclidean group element given by (3.6). Invariantization of the coordinate functions, which is done
Theorem 4.3. If S ⊂ M is a fully regular p-dimensional submanifold of differential invariant rank t, then its symmetry group GS is an (r − t)–dimensional subgroup of G that acts locally freely on S.
A submanifold with maximal differential invariant rank t = p, and hence only a discrete symmetry group, is called nonsingular. The number of symmetries of a nonsingular submanifold is determined by its index , which is defined as the number of points in S map to a single generic point of its signature:
ind S = min
∣ ζ^ ∈ S(s+1)^
Theorem 4.4. If S is a nonsingular submanifold, then its symmetry group is a discrete subgroup of cardinality ind S.
At the other extreme, a rank 0 or maximally symmetric submanifold, [ 82 ], has all constant differential invariants, and so its signature degenerates to a single point.
Theorem 4.5. A regular p-dimensional submanifold S has differential invariant rank 0 if and only if its symmetry group is a p-dimensional subgroup H ⊂ G and hence S is an open submanifold of an H–orbit: S ⊂ H · z 0.
Remark : “Totally singular” submanifolds may have even larger, non-free symmetry groups, but these are not covered by the preceding results. See [ 76 ] for details, including Lie algebraic characterizations.
Remark : See [ 72 ] for some counterexamples when one tries to relax the regularity assumptions in the above results.
Example 4.6. The Euclidean signature for a curve C ⊂ M = R^2 is the planar curve S(C) = { (κ, κs) } parametrized by the curvature invariant κ and its first derivative with respect to arc length. Two fully regular planar curves are equivalent under an oriented rigid motion if and only if they have the same signature curve. The maximally symmetric curves have constant Euclidean curvature, and so their signature curve degenerates to a single point. These are the circles and straight lines, and, in accordance with Theorem 4.5, each is the orbit of its one-parameter symmetry subgroup of SE(2). The number of Euclidean symmetries of a nonsingular curve is equal to its index — the number of times the Euclidean signature is retraced as we go around the curve.
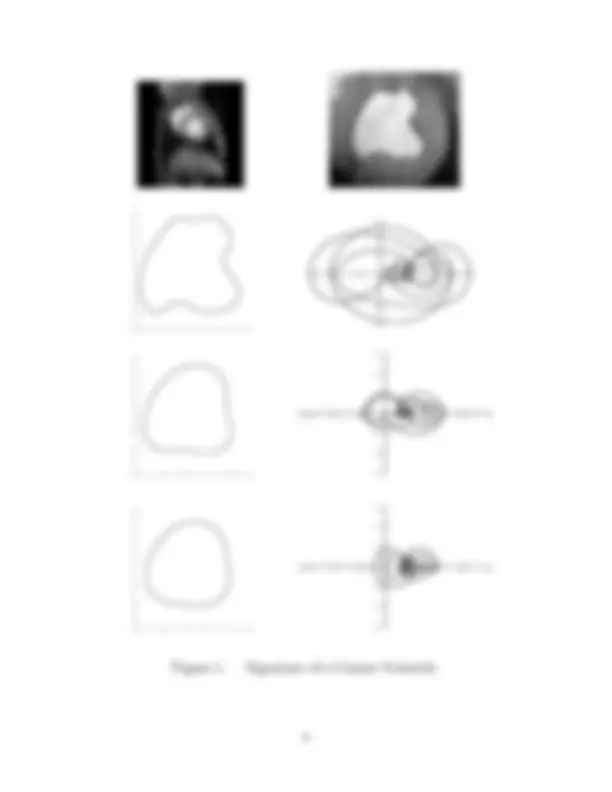
In Figure 1 we display some signature curves computed from the left ventricle of a gray-scale digital MRI scan of a canine heart. The boundary of the ventricle has been automatically segmented through use of the conformally Riemannian snake flow proposed in [ 51 , 96 ]. The ventricle boundary curve is then smoothed with the Euclidean-invariant curve shortening flow (see the final section for details) and the Euclidean signatures of the resulting curves computed. As the progressively smoothed curves approach circularity, their signatures exhibit less variation in curvature and wind more and more tightly around a single point, which is the signature of a circle of area equal to the area inside the evolving curve. Despite the rather extensive smoothing involved, except for an overall shrinking as the contour approaches circularity, the basic qualitative features of the different signature curves appear to be remarkably robust.
10 20 30 40 50 60
20
30
40
50
60
-0.15 -0.1 -0.05 0.05 0.1 0.15 0.
-0.
-0.
-0.
10 20 30 40 50 60
20
30
40
50
60
-0.15 -0.1 -0.05 0.05 0.1 0.15 0.
-0.
-0.
-0.
10 20 30 40 50 60
20
30
40
50
60
-0.15 -0.1 -0.05 0.05 0.1 0.15 0.
-0.
-0.
-0.
z 0 z 1
z 2 z 3
a
b d (^) c e
f
Figure 2. Four-Point Euclidean Curve Invariants.
which parametrize the joint signature Ŝ = Ŝ (C) that uniquely characterizes the curve C up to Euclidean motion. Since this signature avoids any differentiation, it is insensitive to noisy image data. There are two local syzygies
Φ 1 (a, b, c, d, e, f ) = 0, Φ 2 (a, b, c, d, e, f ) = 0, (5.7)
among the the six interpoint distances. One of these is the universal Cayley–Menger syzygy
det
2 a^2 a^2 + b^2 − d^2 a^2 + c^2 − e^2 a^2 + b^2 − d^2 2 b^2 b^2 + c^2 − f 2 a^2 + c^2 − e^2 b^2 + c^2 − f 2 2 c^2
which is valid for all possible planar configurations of the four points, cf. [ 8 ]. The second syzygy in (5.7) is curve-dependent and serves to effectively characterize the joint invariant signature.
A variety of additional examples, including curves and surfaces in two and three- dimensional space under the Euclidean, equi-affine, affine and projective groups, are inves- tigated in detail in [ 77 ].
In modern numerical analysis, the development of numerical schemes that incorpo- rate additional structure enjoyed by the problem being approximated, e.g., symmetries, conservation laws, symplectic structure, etc., is now known as geometric numerical inte- gration, [ 18 , 29 , 40 , 65 ]. In practical applications of invariant theory to computer vision, group-invariant numerical schemes to approximate differential invariants have been ap- plied to the problem of symmetry-based object recognition, [ 10 , 20 , 19 ]. In this section., I discuss the use of moving frame methods to construct symmetry-preserving numerical approximations.
The first step is to construct a suitable manifold that incorporates both the differential equation under consideration and its numerical approximations. Currently, only the case of ordinary differential equations, involving p = 1 independent variables, is completely understood, and so we restrict ourselves to this context.
Finite difference approximations to the derivatives of a function u = f (x) rely on its values u 0 = f (x 0 ),... , un = f (xn) at several distinct points zi = (xi, ui) = (xi, f (xi)) on the graph. Thus, discrete approximations to jet coordinates on Jn^ are functions F (z 0 ,... , zn) defined on the (n + 1)-fold Cartesian product space M ×(n+1). As the points z 0 ,... , zn coalesce, the approximation F (z 0 ,... , zn) will not be well-defined unless we specify the “direction” of convergence. Thus, strictly speaking, F is not defined on all of M ×(n+1), but, rather, on the “off-diagonal” part
M ⋄(n+1)^ =
(z 0 ,... , zn)
∣ (^) zi 6 = zj for all i 6 = j
⊂ M ×(n+1).
As two or more points come together, the limiting value of F (z 0 ,... , zn) will be governed by the derivatives (or jet) of the appropriate order governing the direction of convergence. This motivates our construction of the nth^ order multi-space M (n).
Definition 6.1. An (n + 1)-pointed curve C = (z 0 ,... , zn; C) consists of a smooth curve C and n + 1 not necessarily distinct points z 0 ,... , zn ∈ C thereon. Two (n + 1)-
pointed curves C = (z 0 ,... , zn; C), C˜ = (˜z 0 ,... , ˜zn; C˜), have nth^ order multi-contact if
and only if zi = ˜zi, and j#i− 1 C|zi = j#i− 1 C˜|zi , where #i = #{ j | zj = zi }, for each i = 0,... , n.
Definition 6.2. The nth^ order multi-space, denoted M (n)^ is the set of equivalence classes of (n + 1)-pointed curves in M under the equivalence relation of nth^ order multi- contact. The equivalence class of an (n + 1)-pointed curves C is called its nth^ order multi-jet, and denoted jnC ∈ M (n).
We can identify the subset of multi-jets of multi-pointed curves having distinct points with the off-diagonal Cartesian product space M ⋄(n+1)^ ⊂ Jn. On the other hand, the multi-space equivalence relation reduces to the ordinary jet space equivalence relation on the set of coincident multi-pointed curves, and in this way Jn^ ⊂ M (n). Intermediate cases, when some but not all points coincide, correspond to “off-diagonal” Cartesian products of jet spaces
Jk^1 ⋄ · · · ⋄ Jki^ ≡
(z 0 (k 1 ),... , z( i ki^ )) ∈ Jk^1 × · · · × Jki
∣ π(z ν(k ν^ )) are distinct
where
kν = n and π: Jk^ → M is the usual jet space projection. Theorem 6.3. If M is a smooth m-dimensional manifold, then its nth^ order multi- space M (n)^ is a smooth manifold of dimension (n + 1)m, which contains the off-diagonal part M ⋄(n+1)^ of the Cartesian product space as an open, dense submanifold, and the nth order jet space Jn^ as a smooth submanifold.
Just as local coordinates on Jn^ are provided by the coefficients of Taylor polynomials, local coordinates on M (n)^ are provided by the coefficients of interpolating polynomials, which are the classical divided differences of numerical interpolation theory, [ 78 ].
Definition 6.4. Given an (n + 1)-pointed graph C = (z 0 ,... , zn; C), its divided differences are defined by [ zj ]C = f (xj ), and
[ z 0 z 1... zk− 1 zk ]C = lim z→zk
[ z 0 z 1 z 2... zk− 2 z ]C − [ z 0 z 1 z 2... zk− 2 zk− 1 ]C x − xk− 1
and their divided differences
I(k)^ = ι( [ z 0 z 1... zk ] ) = [ I 0... Ik ] =
[ I 0... Ik− 2 Ik ] − [ I 0... Ik− 2 Ik− 1 ] Hk − Hk− 1
Example 6.6. For the planar Euclidean action (3.2), the multi-prolonged action is locally free on M (n)^ for n ≥ 1. We can thereby determine a first order multi-frame and use it to completely classify Euclidean multi-invariants. The first order transformation formulae are
y 0 = x 0 cos φ − u 0 sin φ + a, v 0 = x 0 sin φ + u 0 cos φ + b,
y 1 = x 1 cos φ − u 1 sin φ + a, v(1)^ =
sin φ + u(1)^ cos φ cos φ − u(1)^ sin φ
where u(1)^ = [ z 0 z 1 ] = (u 1 − u 0 )/(x 1 − x 0 ). Normalization based on the cross-section y 0 = v 0 = v 1 = 0 results in the right moving frame
a = −x 0 cos φ + u 0 sin φ = −
x 0 + u(1)^ u 0 √ 1 + (u(1))^2
b = −x 0 sin φ − u 0 cos φ =
x 0 u(1)^ − u 0 √ 1 + (u(1))^2
tan φ = −u(1)^. (6.8)
Substituting the moving frame formulae (6.8) into the lifted divided differences produces a complete system of (oriented) Euclidean multi-invariants. These are easily computed by beginning with the fundamental joint invariants
Hk = ι(xk) =
(xk − x 0 ) + u(1)^ (uk − u 0 ) √ 1 + (u(1))^2
= (xk − x 0 )
1 + [ z 0 z 1 ] [ z 0 zk ] √ 1 + [ z 0 z 1 ]^2
Kk = ι(uk) =
(uk − u 0 ) − u(1)^ (xk − x 0 ) √ 1 + (u(1))^2
= (xk − x 0 )
[ z 0 zk ] − [ z 0 z 1 ] √ 1 + [ z 0 z 1 ]^2
The higher order multi-invariants are obtained by forming divided difference quotients
[ I 0 Ik ] =
Kk − K 0 Hk − H 0
Kk Hk
(xk − x 1 )[ z 0 z 1 zk ] 1 + [ z 0 zk ] [ z 0 z 1 ]
where, in particular, I(1)^ = [ I 0 I 1 ] = 0. The second order multi-invariant
2 [ z 0 z 1 z 2 ]
1 + [ z 0 z 1 ]^2 ( 1 + [ z 0 z 1 ] [ z 1 z 2 ]
1 + [ z 0 z 1 ] [ z 0 z 2 ]
u(2)
1 + (u(1))^2 [ 1 + (u(1))^2 + 12 u(1)u(2)(x 2 − x 0 )
1 + (u(1))^2 + 12 u(1)u(2)(x 2 − x 1 )
provides a Euclidean–invariant numerical approximation to the Euclidean curvature:
lim z 1 ,z 2 →z 0 I(2)^ = κ =
u(2) (1 + (u(1))^2 )^3 /^2
−4 −3 −2 −1 0
−
−
−
−
−
−
−
−
−
−
(a) Starting at x = 5
Log(Step Size)
Log(Error)
−4 −3 −2 −1 0
−
−
0
5
10
15
20
(b) Starting at x = 0.
Log(Step Size)
Log(Error)
RK IRK RK IRK
Figure 3. Invariantized Runge–Kutta Schemes for Ames’ Equation.
Similarly, the third order multi-invariant
will form a Euclidean–invariant approximation for the normalized differential invariant κs = ι(uxxx), the derivative of curvature with respect to arc length, [ 20 , 31 ]. In [ 26 ], my undergraduate student Derek Dalle makes detailed comparisons between the various divided difference approximations to differential invariants, and shows a number of advan- tages of such moving frame-based approximations.
Given a symmetry group of an ordinary differential equation, we can construct a mov- ing frame on the associated multispace and apply the induced invariantization procedure to standard numerical schemes, e.g., Runge–Kutta methods, to systematically derive invari- antized schemes that respect the symmetries. As emphasized by Pilwon Kim, [ 52 , 53 , 54 ], the key to the success of the invariantized numerical scheme lies in the intelligent choice of cross-section for the moving frame. Let us look at one simple illustrative example taken from [ 52 ].
Example 6.7. Ames’ equation
uxx = −
ux x
− eu^ (6.9)
is a well-studied stiff ordinary differential equation that arises in a wide range of fields, including kinetics and heat transfer, vortex motion of incompressible fluids, and the mass distribution of gaseous interstellar material under influence of its own gravitational fields,
d = πH ◦^ d + πV ◦^ d = dH + dV , which results in the variational bicomplex on J∞. If F (x, u(n)) is any differential function, its horizontal differential is
dH F =
∑^ p
i=
(DiF ) dxi, (7.2)
in which Di = Dxi denote the usual total derivatives with respect to the independent variables. Thus, dH F can be identified with the “total gradient” of F. Similarly, its vertical differential is
dV F =
α,J
∂uαJ
θαJ =
α,J
∂uαJ
DJ θα^ = DF (θ), (^) (7.3)
in which the total derivatives act as Lie derivatives on the contact forms θ = (θ^1 ,... , θq)T^ , and DF denotes the formal linearization operator or Fr´echet derivative of the differential function F. Thus, the vertical differential dV F can be identified†^ with the (first) variation, hence the name “variational bicomplex”.
Let πn: J∞^ → Jn^ be the natural jet space projections. Choosing a cross-section Kn^ ⊂ Vn^ ⊂ Jn, we extend the induced nth^ order moving frame ρ(n)^ to the infinite jet bundle by setting ρ(x, u(∞)) = ρ(n)(x, u(n)) whenever (x, u(n)) = πn(x, u(∞)) lies in the domain of definition of ρ(n). We will employ our moving frame to invariantize the vari- ational bicomplex. As before, the invariantization of a differential form is the unique invariant differential form that agrees with its progenitor on the cross-section. In particu- lar, the invariantization process does not affect invariant differential forms. In practice, one determines the invariantization by first transforming the differential form by the prolonged group action and then substituting the moving frame formulae for the group parameters.
As in (3.1), the fundamental differential invariants are obtained by invariantizing the jet coordinates: Hi^ = ι(xi), IJα = ι(uαJ ). Let
̟^ i^ = ι(dxi) = ωi^ + ηi, where (^) ωi^ = πH (̟ i), ηi^ = πV (̟ i), (7.4)
denote the invariantized horizontal one-forms. Their horizontal components ω^1 ,... , ωp prescribe, in the language of [ 74 ], a contact-invariant coframe for the prolonged group ac- tion, while the contact forms η^1 ,... , ηp^ are required to make ̟^1 ,... ,̟ p^ fully G-invariant. Finally, the invariantized basis contact forms are denoted by
ϑαJ = ι(θαJ ), α = 1,... , q, #J ≥ 0. (7.5)
Invariantization of more general differential forms relies on the fact that it preserves the exterior algebra structure, and so
ι(Ω + Ψ) = ι(Ω) + ι(Ψ), ι(Ω ∧ Ψ) = ι(Ω) ∧ ι(Ψ), (7.6)
for any differential forms (or functions) Ω, Ψ on J∞.
† (^) This becomes clearer when you rewrite θα J =^ δu α J.
As in the ordinary bicomplex construction, the decomposition of invariant one-forms on J∞^ into invariant horizontal and invariant contact components induces a decomposition of the differential. However, now d = dH + dV + dW splits into three constituents, where dH adds an invariant horizontal form, dV adds a invariant contact form, while dW replaces an invariant horizontal one-form with a combination of wedge products of two invariant contact forms. They satisfy the “quasi-tricomplex” identities
d^2 H = 0, dH dV + dV dH = 0, d^2 W = 0, dV dW + dW dV = 0,
d^2 V + dH dW + dW dH = 0. (7.7)
Fortunately, the third, anomalous component dW plays no role (to date) in the applica- tions; in particular, dW F = 0 for any differential function F. Even better, if the group acts projectably, dW ≡ 0. The corresponding dual invariant differential operators D 1 ,... , Dp are then defined so that
dH F =
∑^ p
i=
(DiF ) ̟ i, dH Ω =
∑^ p
i=
̟^ i^ ∧ Di Ω, (^) (7.8)
for any differential function F and, more generally, differential form Ω, on which the Di act via Lie differentiation. Keep in mind that, in general, the invariant differential operators do not commute; see (7.17) below. The most important fact underlying the moving frame construction is that, while it does preserve algebraic structure, the invariantization map ι does not respect the dif- ferential. The recurrence formulae, [ 31 , 57 ], which we now review, provide the missing “correction terms”, i.e., dι(Ω) − ι(dΩ). Remarkably, they can be explicitly and algorithmi- cally constructed using merely linear differential algebra — without knowing the explicit formulas for either the differential invariants or invariant differential forms, the invariant differential operators, or even the moving frame!
Let v 1 ,... , vr be a basis for the infinitesimal generators of our transformation group. For conciseness, we will retain the same notation for the corresponding prolonged vector fields on J∞^ which, in local coordinates, take the form
vκ =
∑^ p
i=
ξiκ(x, u)
∂xi^
∑^ q
α=
j=#J≥ 0
ϕαJ,κ(x, u(j))
∂uαJ
, κ = 1,... , r. (7.9)
The coefficients ϕαJ,κ = vκ(uαJ ) can be successively constructed by Lie’s recursive prolon- gation formula, [ 73 , 74 ]:
ϕαJi,κ = DiϕαJ,κ −
∑^ p
j=
uαJj Diξκj. (7.10)
With this in hand, we can formulate the universal recurrence formula.
Theorem 7.1. If Ω is any differential function or form on J∞, then
d ι(Ω) = ι(d Ω) +
∑^ r
κ=
νκ^ ∧ ι [vκ(Ω)], (7.11)
where
Y (^) jki = − Y (^) kji =
∑^ r
κ=
Rκk ι(Dj ξiκ) − Rκj ι(Dk ξκi)
are called the commutator invariants, since they prescribe the commutators of the invariant differential operators:
[ Dj , Dk ] =
∑^ p
i=
Y (^) jki Di. (7.17)
The terms in (7.15) involving wedge products of a horizontal and a contact form yield
dV ̟ i^ =
∑^ r
κ=
[ (^) q ∑
α=
ι
∂ξiκ ∂uα
Rκj ̟ i^ ∧ ϑα^ −
∑^ p
k=
ι(Dk ξκi) Sακ,J ̟ k^ ∧ ϑαJ
Finally, the remaining terms, involving wedge products of two contact forms, provide the formulas for the anomalous third component of the differential:
dW ̟ i^ =
∑^ r
κ=
∑^ q
α=
ι
∂ξiκ ∂uα
Sακ,J ϑαJ ∧ ϑα. (7.19)
In a similar fashion, we derive the recurrence formulae (7.11) for the differentiated invariant contact forms: In particular, the horizontal components
DiϑαJ = ϑαJi +
∑^ r
κ=
Rκi ι
vκ(θαJ )
can be inductively solved to express the higher order invariantized contact forms as certain invariant derivatives of those of order 0:
ϑαJ = EJα (ϑ) =
∑^ q
β=
EJ,βα (ϑβ^ ), (7.21)
in which ϑ = (ϑ^1 ,... , ϑq)T^ denotes the column vector containing the order zero invari- antized contact forms, while EJα = (EJ,α 1 ,... , EJ,qα ) is a row vector of invariant differential
operators, i.e., each EJ,α =
AKJ,αDK^ for certain differential invariants AKJ,α. Combining these formulae allows us to express the invariant vertical derivative or invariant variation of any differential invariant K in the form
dV K = AK (ϑ), (7.22)
in which AK is a row vector of invariant differential operators. Formula (7.22) can be viewed as the invariant version of the vertical differentiation formula (7.3), and so will refer to AK as the invariant linearization operator associated with the differential invariant K. Similarly, we derive the recurrence formulae for the vertical differentials of the invariant horizontal forms:
dV ̟ i^ =
∑^ p
j=
∑^ q
α=
Bijα(ϑα) ∧ ̟ j^ =
∑^ p
j=
Bij (ϑ) ∧ ̟ j^ (7.23)
in which Bij = (Bij 1 ,... , Bijq ) is a family of p^2 row-vector-valued invariant differential operators, known, collectively, as the invariant Hamiltonian operator complex , stemming from its role in the calculus of variations, cf. [ 57 , 88 ].
Example 7.3. Let us return to the Euclidean group acting on plane curves initiated in Example 3.1. The basic invariant horizontal one-form ̟ = ι(dx) is obtained by first transforming dx by a general group element:
dx 7 −→ dy = (cos φ − ux sin φ) dx + (sin φ)θ, (7.24)
where θ = du − ux dx, θx = dux − uxx dx,... , (7.25)
are the ordinary basis contact forms. Substituting the moving frame formulae (3.6) for the group parameters into (7.24) yields the basic invariant horizontal one-form
̟ = ι(dx) =
dx + ux du √ 1 + u^2 x
1 + u^2 x dx +
ux √ 1 + u^2 x
θ. (7.26)
Its (non-invariant) horizontal component is the contact-invariant arc length form
ω = πH (̟ ) = ds =
1 + u^2 x dx,
and so the corresponding invariant differential operator is the usual arc length derivative D = Ds. In the same manner we obtain the basis invariant contact forms
ϑ = ι(θ) =
θ √ 1 + u^2 x
, ϑ 1 = ι(θx) =
(1 + u^2 x) θx − uxuxxθ (1 + u^2 x)^2
To construct the recurrence formulae for the differentiated functions and forms, we begin with the prolonged infinitesimal generators of SE(2):
v 1 = ∂x, v 2 = ∂u, v 3 = − u ∂x + x ∂u + (1 + u^2 x) ∂ux + 3 uxuxx ∂uxx + (4 uxuxxx + 3 u^2 xx) ∂uxxx + · · ·.
The pulled back dual Maurer–Cartan forms ν^1 , ν^2 , ν^3 are found by applying the universal recurrence formulae (7.11) to the phantom invariants:
0 = dH = ι(dx) + ι(v 1 (x)) ν^1 + ι(v 2 (x)) ν^2 + ι(v 3 (x)) ν^3 = ̟ + ν^1 , 0 = dI 0 = ι(du) + ι(v 1 (u)) ν^1 + ι(v 2 (u)) ν^2 + ι(v 3 (u)) ν^3 = ϑ + ν^2 , 0 = dI 1 = ι(dux) + ι(v 1 (ux)) ν^1 + ι(v 2 (ux)) ν^2 + ι(v 3 (ux)) ν^3 = κ̟ + ϑ 1 + ν^3 ,
since du = ux dx + θ, dux = uxx dx + θx. Therefore,
ν^1 = −̟ , ν 2 = − ϑ, ν^3 = − κ̟ − ϑ 1. (7.28)
We are now ready to substitute the non-phantom invariants into (7.11):
dκ = dι(uxx) = ι(duxx) + ι(v 1 (uxx)) ν^1 + ι(v 2 (uxx)) ν^2 + ι(v 3 (uxx)) ν^3 = ι(uxxx dx + θxx) − ι(3 uxuxx) (κ̟ + ϑ 1 ) = I 3 ̟ + ϑ 2 , dI 3 = dι(uxxx) = ι(duxxx) + ι(v 1 (uxxx)) ν^1 + ι(v 2 (uxxx)) ν^2 + ι(v 3 (uxxx)) ν^3 = ι(uxxxx dx + θxxx) − ι(4 uxuxxx + 3u^2 xx) (κ̟ + ϑ 1 ) = (I 4 − 3 κ^3 )̟ + ϑ 3 − 3 κ^2 ϑ 1 ,