Vectors in Three-Dimensional Space: Concepts and Formulas - Prof. J. R. Buchanan, Assignments of Advanced Calculus

Download Vectors in Three-Dimensional Space: Concepts and Formulas - Prof. J. R. Buchanan and more Assignments Advanced Calculus in PDF only on Docsity!

Vectors in Space

MATH 311, Calculus III

J. Robert Buchanan

Department of Mathematics

Fall 2007

Three-dimensional Space R^3

Ordered triples ( a , b , c ) Right-handed coordinate system Octants Coordinate planes

Vectors in R^3

The space of all vectors in R^3 will be denoted V 3.

V 3 = {〈 x , y , z 〉 : x , y , z ∈ R}

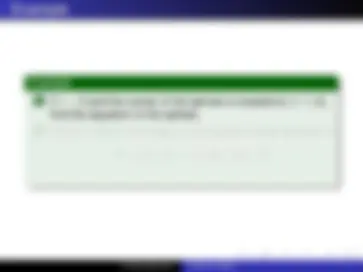
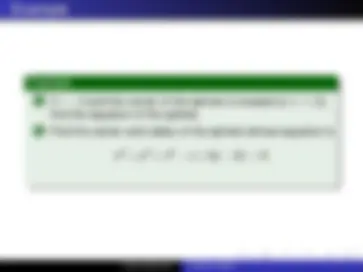
The vector with initial point P 1 = ( x 1 , y 1 , z 1 ) and terminal point P 2 = ( x 2 , y 2 , z 2 ) is −−−→ P 1 P 2 = 〈 x 2 − x 1 , y 2 − y 1 , z 2 − z 1 〉

Vectors in R^3

The space of all vectors in R^3 will be denoted V 3.

V 3 = {〈 x , y , z 〉 : x , y , z ∈ R}

The vector with initial point P 1 = ( x 1 , y 1 , z 1 ) and terminal point P 2 = ( x 2 , y 2 , z 2 ) is −−−→ P 1 P 2 = 〈 x 2 − x 1 , y 2 − y 1 , z 2 − z 1 〉

Examples

Example Let a = 〈 2 , 4 , − 1 〉 and b = 〈 5 , − 4 , 3 〉 and calculate the following. (^1) a + b (^2) ‖ b ‖ (^3 3) a − 2 b

Special Vectors

(^1) Zero vector: 0 = 〈 0 , 0 , 0 〉 (^2) Standard basis vectors: i = 〈 1 , 0 , 0 〉 j = 〈 0 , 1 , 0 〉 k = 〈 0 , 0 , 1 〉

Any vector a in V 3 can be written as

a = 〈 a 1 , a 2 , a 3 〉 = a 1 i + a 2 j + a 3 k.

Unit Vectors and Midpoints

For any a 6 = 0 the vector of length one (unit vector) in the same direction as a is given by

u =

‖ a ‖

a.

The midpoint of the line segment joining points P 1 = ( x 1 , y 1 , z 1 ) and P 2 = ( x 2 , y 2 , z 2 ) is given by ( x 1 + x 2 2

y 1 + y 2 2

z 1 + z 2 2

Unit Vectors and Midpoints

For any a 6 = 0 the vector of length one (unit vector) in the same direction as a is given by

u =

‖ a ‖

a.

The midpoint of the line segment joining points P 1 = ( x 1 , y 1 , z 1 ) and P 2 = ( x 2 , y 2 , z 2 ) is given by ( x 1 + x 2 2

y 1 + y 2 2

z 1 + z 2 2

Equation of a Sphere

A sphere is the set of all points in R^3 whose distance from a fixed point ( a , b , c ) called the center is r > 0 called the radius.

( x − a )^2 + ( y − b )^2 + ( z − c )^2 = r

( x − a )^2 + ( y − b )^2 + ( z − c )^2 = r^2

Example

Example (^1) If r = 2 and the center of the sphere is located at ( 1 , 1 , 2 ), find the equation of the sphere. (^2) Find the center and radius of the sphere whose equation is

x^2 + y^2 + z^2 − x + 2 y − 2 z = 0.

Homework

Read Section 10.2. Pages 802–804: 1–63 odd.