Linear Algebra I - Solving Linear Equations and Matrix Operations, Study notes of Linear Algebra

Download Linear Algebra I - Solving Linear Equations and Matrix Operations and more Study notes Linear Algebra in PDF only on Docsity!

Lecture 17

Linear Algebra I

Outline

• Motivation
  • Linear equations, Linear systems
• Vectors
  • Length, Dot Product
• Matrices
  • Matrix Vector Product, Matrix Multiplication
• Solving systems of linear equations

Linear Equations

• y = mx+b is a linear function
• Setting mx + b = c is a linear equation
• A “system” of equations contains multiple equations

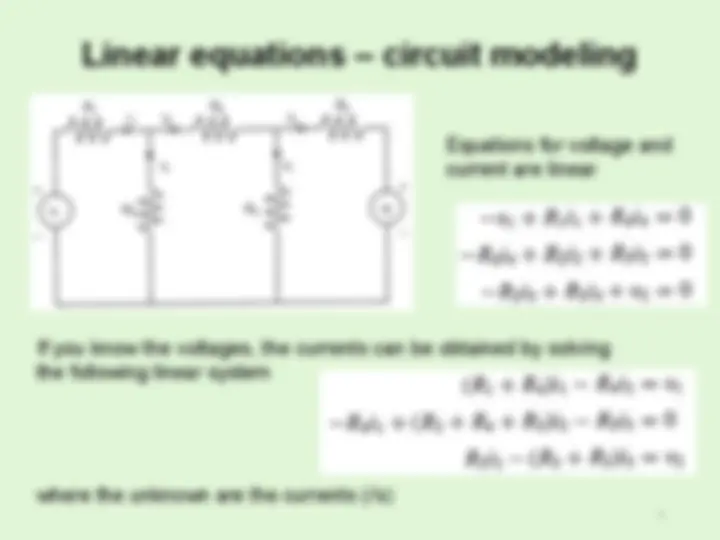
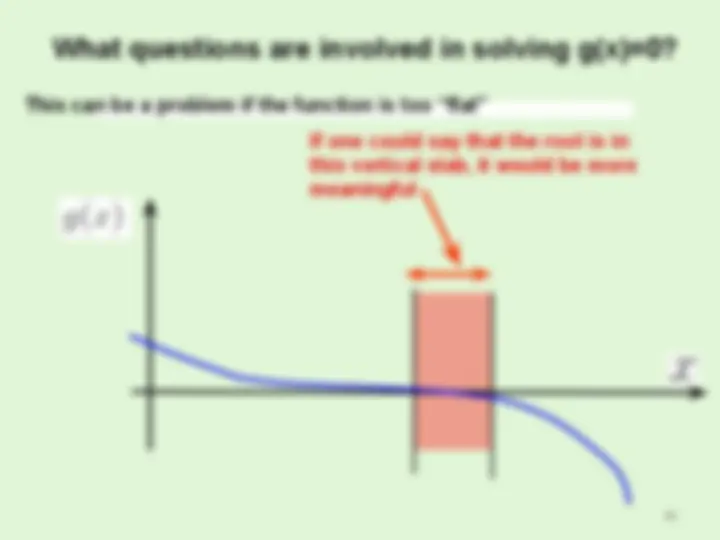
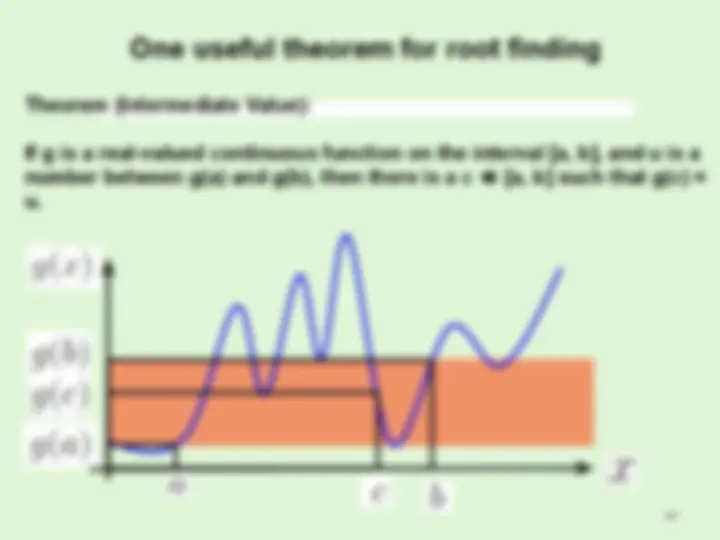
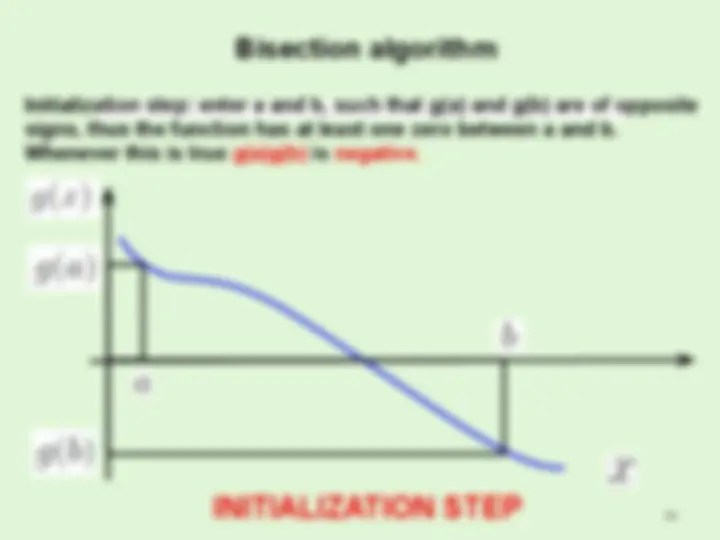
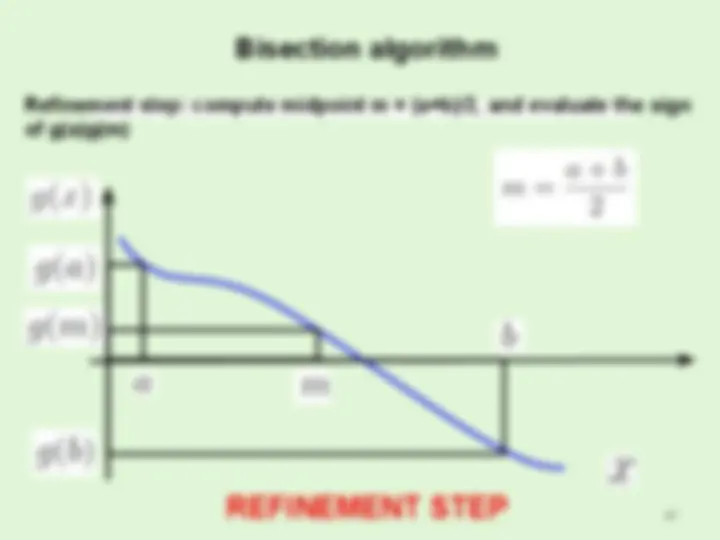
Solving a system of equations involves finding a set values that allow all the equations to hold.

- This is not always possible

Systems of Equations

Examples

Linear Equations: y = mx + b

• One solution
• No solution
• Infinite number of solutions

Disks in the plane (non-linear): (x - x0)^2 + (x - y0)^2 = r

• What are the possibilities?

Linear equations in Matrix Form

m linear equations with n variables:

Can be written in matrix form where

Matrices - Review

• A matrix consists of a rectangular array of elements represented by a single symbol e.g., A
• An individual entry of a matrix is an element e.g., a 23 , can also write A (^23)

Matrix Operations

• isequal(A,B)

Two matrices are considered equal if and only if every element in the first matrix is equal to every corresponding element in the second. This means the two matrices must be the same size.

• A+B, A-B

Matrix addition and subtraction are performed by adding or subtracting the corresponding elements. This requires that the two matrices be the same size.

• A*c

Scalar matrix multiplication is performed by multiplying each element by the same scalar

Matrix-Vector multiplication

If A is an n-by-m matrix, and x is an m-by-1 vector, then the “product Ax ” is a n-by-1 vector, whose i’th component is

n-by-m^ =

m-by-1 n-by-

n-by-m =

m-by-1 (^) n-by-

Example norms

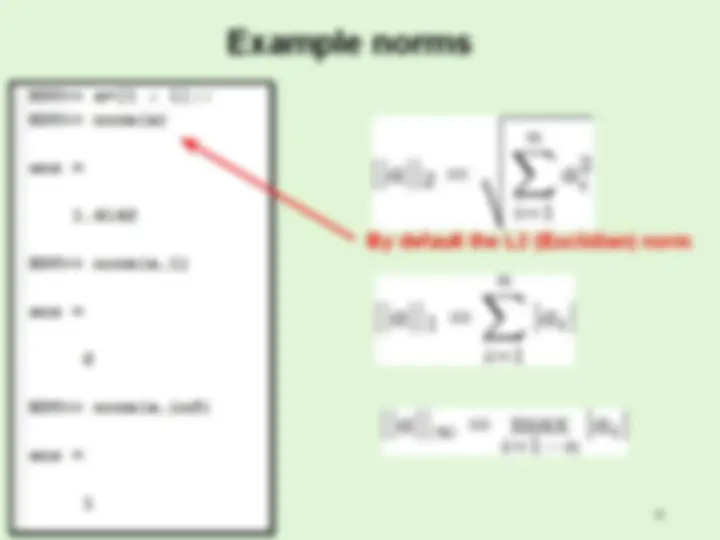
By default the L2 (Euclidian) norm

Dot Product - Definition

Dot Product – Geometric

interpretation

The Dot Product equivalent to

where and are the lengths (L2 norm) of x and y, and is the angle between vectors x and y.

Remark: Derivation can be done in 2D: express x and y in polar form, and take the usual dot product

Dot Product – Geometric

interpretation

When applied to a unit vector the dot product is the length of the projection onto that unit vector, when the two vectors are placed tail to tail.

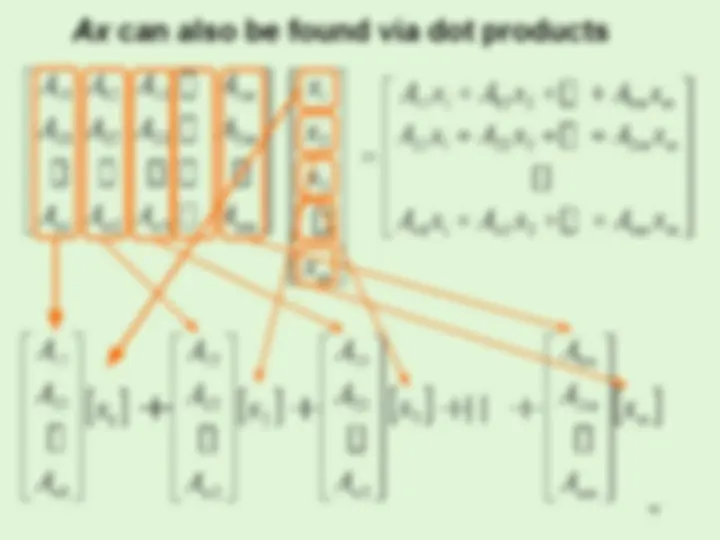
Ax can also be found via dot products

Ax as a collection of dot products

If A is an n-by-m matrix, and x is an m-by-1 vector, then the “product Ax ” is a n-by-1 vector, whose i’th component is