Notes—Chap. 10b Introduction to Numerical Methods
(pp. 413 – 420)
- Provides functions for arithmetic mean, standard deviation, linear regression,
and provides formula for correlation coefficient.
- Arithmetic mean gives the average of values in a set, xi , i = 1, ..., n.
∑ xi
x = arithmetic mean = ────
n
- C++ function that implements arithmetic mean (Figs. 10.5 slightly revised):
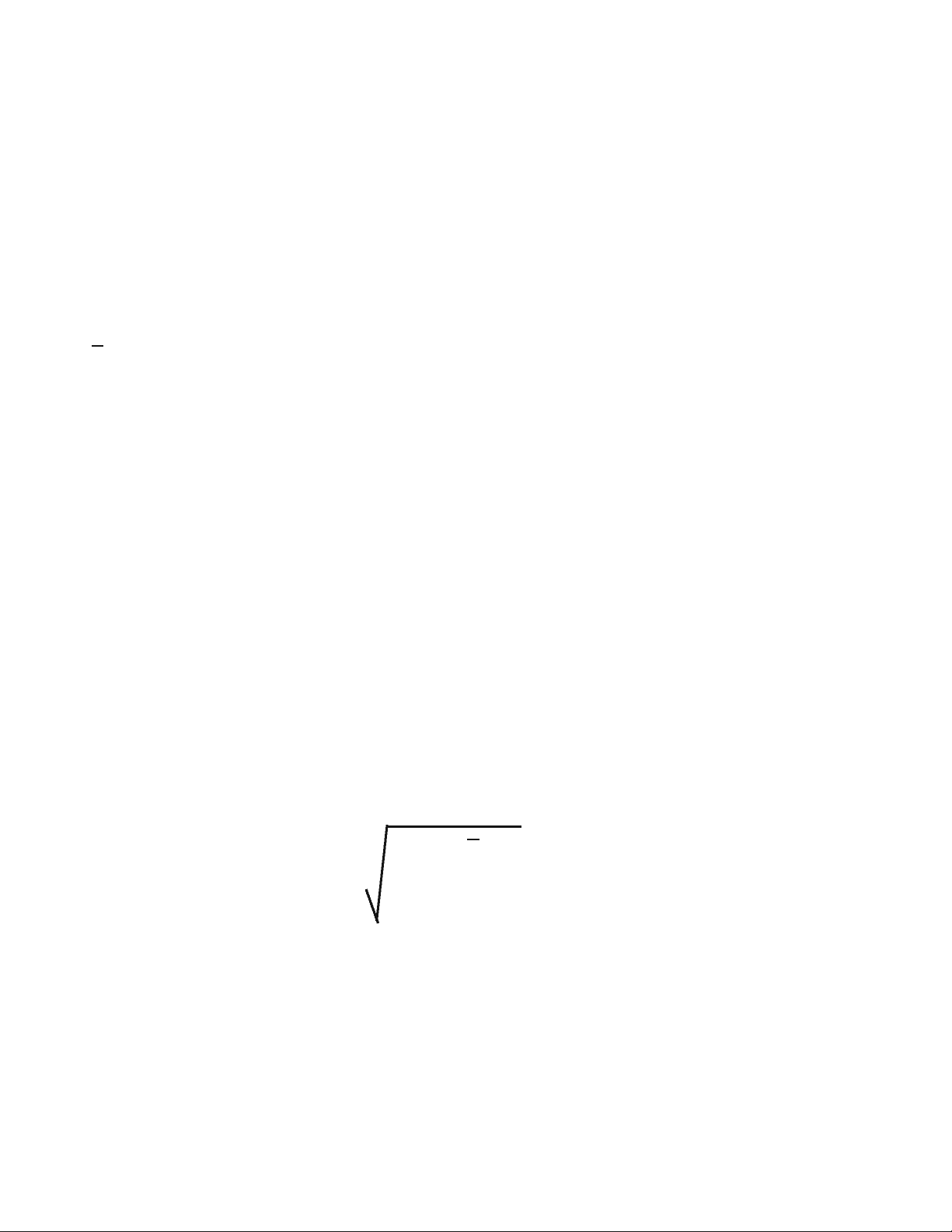
double arithmeticMean(const double x[], int n)
// Compute the arithmetic mean (average) of the first n elements of x.
// Pre: n > 0
{
int i;
double sum = 0; // running sum of elements in list
for (i = 0; i < n; ++i)
sum += x[i];
return (sum / n);
}
- Standard deviation measures the variance of values in a set, xi , i = 1, ..., n.
∑ (xi - x)2
s = standard deviation = ────────
n
- C++ function that implements standard deviation (Figs. 10.7 slightly revised):
#include <cmath>
double arithmeticMean(const double x[], int n);
double stdDev(const double x[], int n)
// Calculate standard deviation of first n elements of x.
// Pre: n > 0
