Download Inductors and Capacitors: Understanding Energy Storage and Power in Electrical Circuits and more Study notes Electrical Circuit Analysis in PDF only on Docsity!
6. Inductance and Capacitance, and Mutual
Inductance
Two new circuit elements
Inductor
An inductor is an electrical component that opposes any
change in electrical current. It is composed of a coil of wire
wound around a supporting core. An inductor can store
energy.
Capacitor
A capacitor is an electrical component that consists of two
conductors separated by an insulator or dielectric material. A
capacitor can store electrical charge.
Inductors and capacitors are classified as passive elements
and they cannot generate energy.
6.1 Inductor
The symbol for impedance is L and measured in henrys [H].
The relationship between the voltage and current at the
terminals of an inductor:
t
t
vd i t L
i t
dt
di v L
0
- If current is constant, the voltage across the ideal
inductor is zero
- Current cannot change instantaneously in the inductor
Example 6.1a
For t<0, i(t)=
For 0<t≤1,
i t d i t
t
0
For 1<t≤2,
1
i t d i t
t
τ
Example 6.1b
5 = >
− i t te t
i t t
t
Find the voltage, power of the inductor. When the current
reaches its maximum?
The maximum value of current is:
te e t s dt
di (^) t t 10 ( 5 ) 0 0. 2
5 5 = − + = → =
− −
Voltage on the inductor
5 5 5 = = − + = − >
− − − te e e t V t dt
di v t L
t t t
p t vi te t e W
10 t 2 10 t ( ) 10 50
− − = = −
t
w pd
0
Figure: The variables for example 6.1b
6.2 Capacitor
It is represented by C and is measured in farads (F). The
relationship between the voltage and current at the terminals
of a capacitor:
0
id v t C
v t
dt
dv i C
t
t
The power is:
dt
dv p = vi = Cv
The energy is:
2
2
w = cv
- A capacitor does not permit an instantaneous change in
its terminal voltage.
- If voltage is constant, a capacitor behaves as an open
circuit.
- Only a time-varying voltage can produce a displacement
current.
Example 6.
t s
tA t s
tA t s
t
i t
Voltage:
For t≤0, v=
For 0<t≤ 20 μs,
v t d t V
t
= ⋅ + =
0
6 9 2 ( ) 5 10 5000 τ τ 0 ( 12. 5 ) 10
For 20<t≤ 40 μs
v t d t t V
t
( ) 5 10 ( 0. 2 5000 ) 5 ( 10 ( 12. 5 ) 10 10 )
20
6 6 9 2 = ⋅ − + = − −
F
or t ≥ 40 μs
v(t)=v(40 μ s)=10V
For t≥ 40 μs
w(t)=?
Example 6.
t
t t
t
i t
For t<
−∞
t
i d C
v t τ τ
For 0 ≤ t<
2
0
2
0 0
t t i d d C
v t v
t
t t
= + = + = =
For t≥ 2
2
2
2
t t
i d d C
v t v τ τ τ
Capacitors in serial
Total capacitor value:
t
t
i d v t C
v t
C C C C
0
0
1 2 3
τ τ
Capacitors in parallel
Total capacitor value:
dt
dv t i t C
C C C C
1 2 3
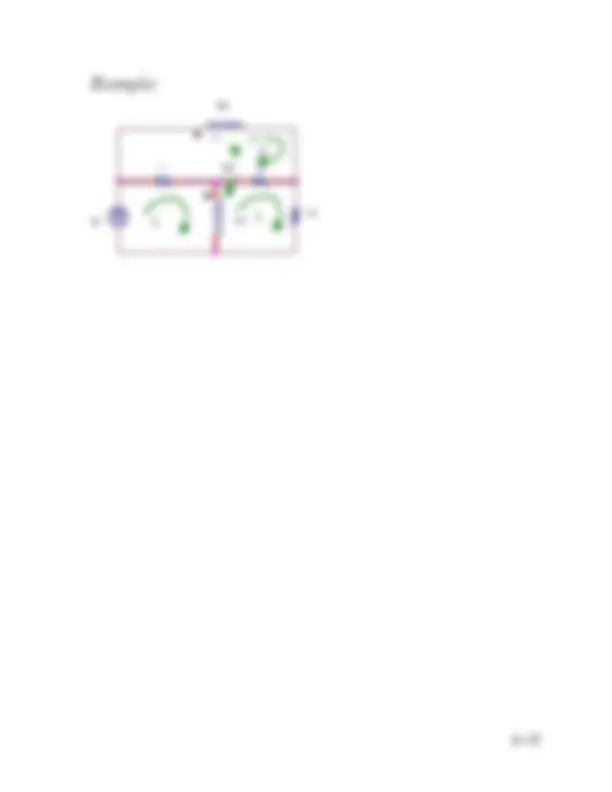
6.4 Mutual Inductance
Inductance/self-inductance: is the parameter that relates a
voltage to a time-varying current in the same circuit.
Mutual inductance: Two circuits are linked by a magnetic
field. If current is time varying in the first circuit, it will be
resulting magnetic field. This magnetic field induces voltage
in the second circuit that related to current in the first circuit
by parameter mutual inductance which is labeled M. Two
coils are labeled L 1 and L 2.
Let’s write the mesh currents equation:
2 1 2 2 2
1 2 1 1 1
dt
di M dt
di i R L
dt
di M dt
di v (^) g iR L
Dot convention: used to keep track the polarity of induced
voltage. When the reference direction for a current enters the
dotted terminal of a coil, the reference polarity of the voltage
that it induces in the other coil is positive at its dotted terminal.
