The University of Portland
School of Engineering
EE352
Electronic Circuits II
HOMEWORK 6
Assigned: Mon, Mar 16, 2009
Due: Wed, Mar 25, 2009
Problems:
1) Text 8.64. Note, solve for ω
180
by hand using “iteration”.
2) Text 8.73.
3) Text 8.81. Use matlab to solve.
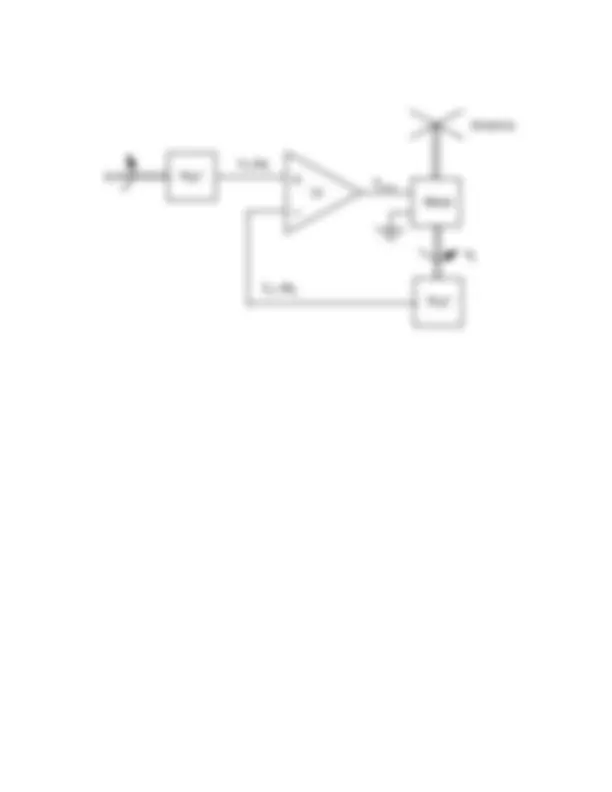
4) A negative feedback servo-system used to rotate a roof-top antenna is
schematically shown in the Figure on the reverse page. This is a “position-
sensitive” feedback system as discussed in class. The two potentiometers convert
the angular positions, θ
i
and θ
o
, to corresponding voltages, V
i
and V
o
, through the
transfer function, V=K
p
θ where K
p
=5V/rad. The output voltage, V
o
, is subtracted
from the input voltage, V
i
, and the result is multiplied by 10V/V through a gain stage
yielding V
error
=10(V
i
-V
o
). V
error
then drives the motor. Assume the following: (1) the
total Moment of Inertia of the entire output mechanism (antenna, antenna shaft,
motor rotor, and potentiometer) is J=2kg-m
2
, (2) the torque provided by the motor is
G=10N-m/A multiplied by the armature current, I
a
(i.e. τ=GI
a
=10I
a
) and, (3) the
motor can be modeled as an armature resistor, R
a
=10Ω, in series with an ω-
dependent voltage generator known as the “Back-EMF Voltage” where V
BEMF
=Gω
as shown in class.
a) Sketch the closed-loop, negative feedback block diagram which relates θ
o
and θ
i
. Find the closed-loop Transfer Function, A
f
(s)=θ
o
(s)/θ
i
(s).
b) Determine the Bode Plots of A
f
(s) using matlab. What is the
“characterisic frequency”, ω
n
, of this electromechancial servo-system ?
c) Plot by hand the location of the closed-loop poles of A
f
(s) in the complex
plane (σ vs jω). By inspection, is the system stable ? If so, is this system
underdamped, overdamped or critically damped ?
d) Calculate the Loop Gain, LG(s) of this servo-system. Determine the
system’s Phase Margin and Gain Margin using matlab.
