




















Study with the several resources on Docsity

Earn points by helping other students or get them with a premium plan


Prepare for your exams
Study with the several resources on Docsity

Earn points to download
Earn points by helping other students or get them with a premium plan
Community
Ask the community for help and clear up your study doubts
Discover the best universities in your country according to Docsity users
Free resources
Download our free guides on studying techniques, anxiety management strategies, and thesis advice from Docsity tutors
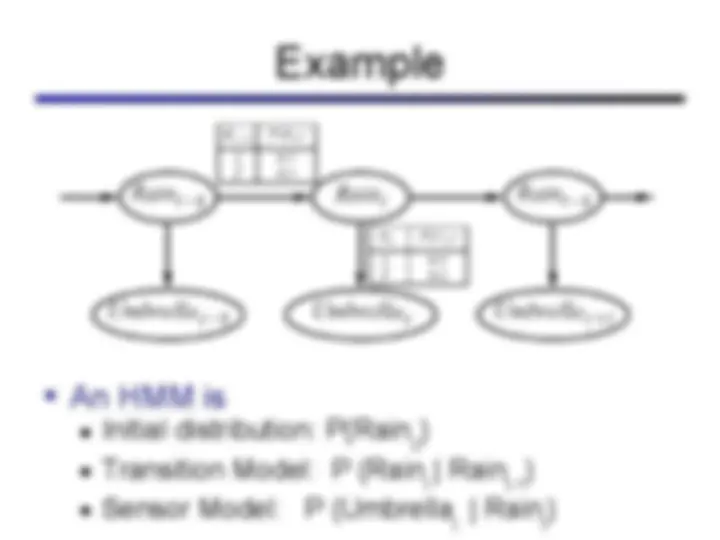
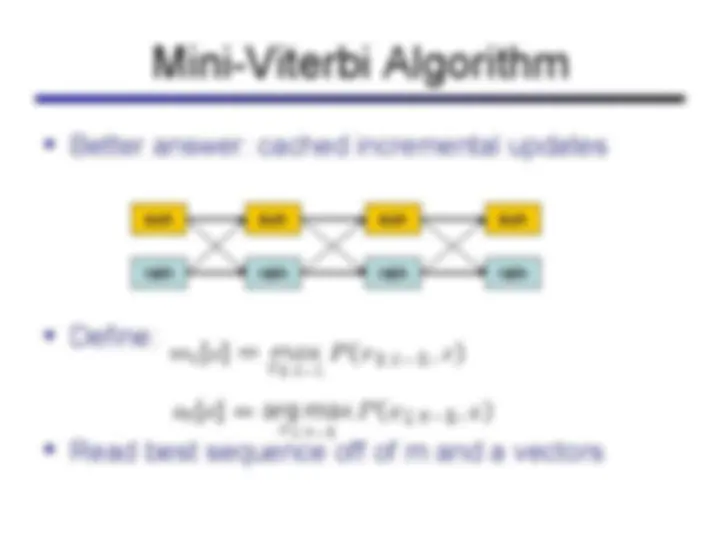
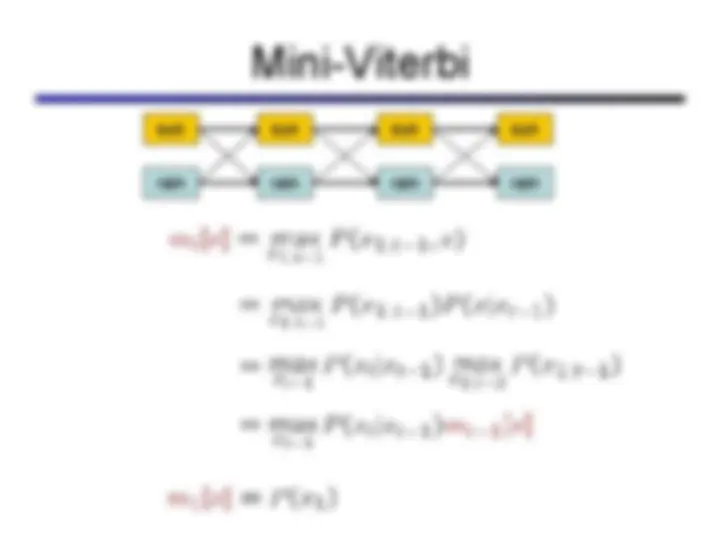
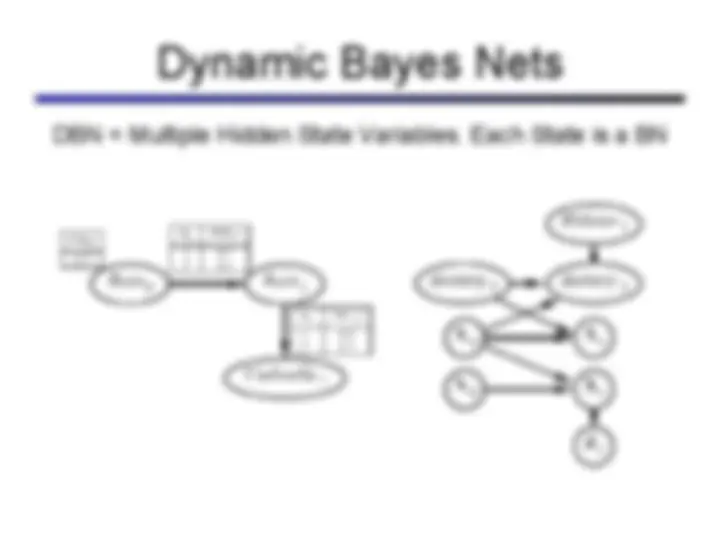
Hidden markov models (hmms), a probabilistic model used for reasoning about sequences of observations. Hmms are particularly useful for problems involving time and uncertainty, such as speech recognition, robot localization, and medical monitoring. The concepts of states, observations, stationary assumption, markov assumption, and the role of hidden variables in hmms. It also covers the forward algorithm and viterbi algorithm for finding the most likely sequence of hidden states given observations.
Typology: Study notes
1 / 34

This page cannot be seen from the preview
Don't miss anything!



























Derek Harter – Texas A&M University – Commerce Slides adapted from Srini Narayanan – ICSI and UC Berkeley
(^) Speech recognition (^) Robot localization (^) User attention (^) Medical monitoring
t
t
t
t
t
t
t
0:t
0:t-
t
t
0
t
t-
t
t
(^) Past and future independent of the present (^) Each time step only depends on the previous (^) This is called the (first order) Markov property
(^) We can always use generic BN reasoning on it (if we truncate the chain)
2
1
3
4
0
1
t
1
t
0
i=1,t
i
i-
i
i
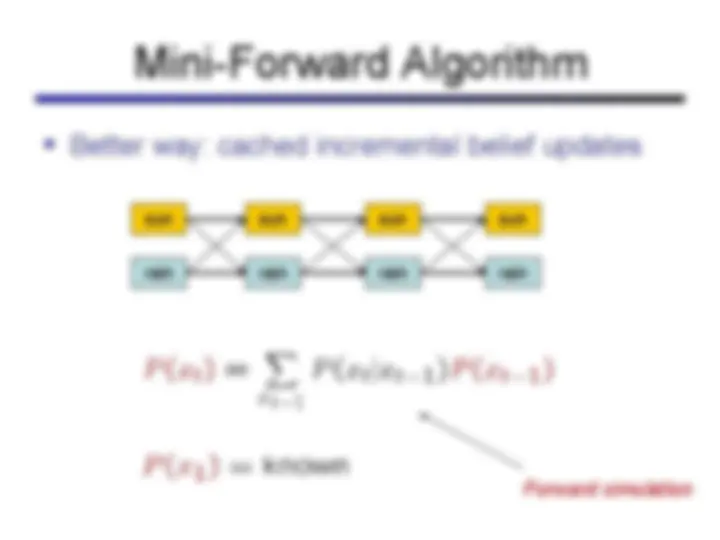
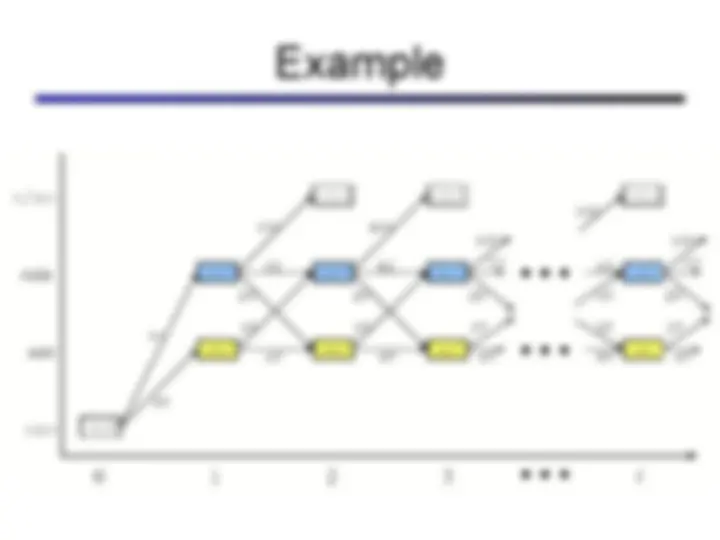
(^) Enumerate all sequences of length t which end in s (^) Add up their probabilities
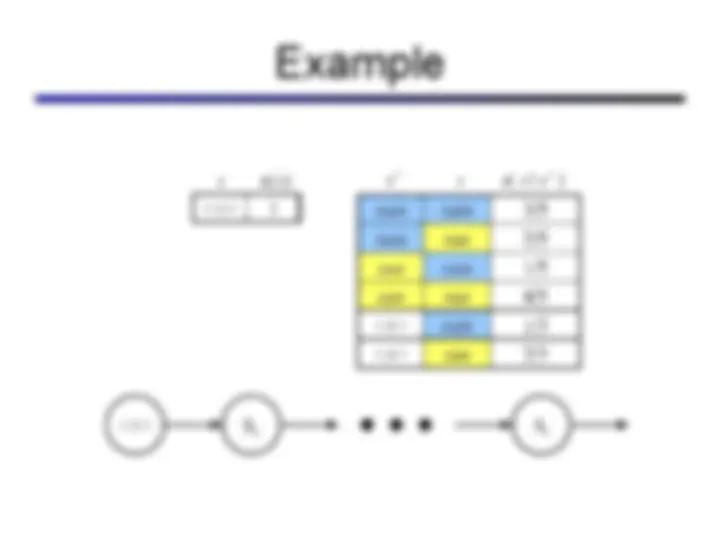
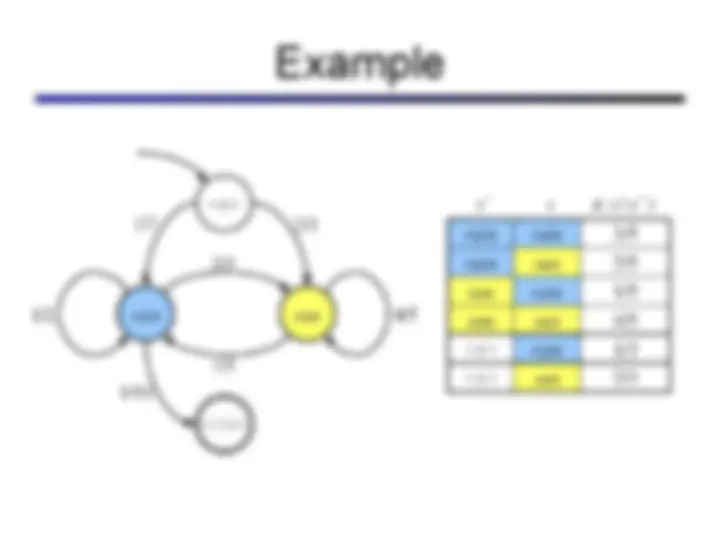
sun rain sun rain sun rain sun rain Forward simulation
(^) What happens? (^) Uncertainty accumulates (^) Eventually, we have no idea what the state is!
(^) For most chains, the distribution we end up in is independent of the initial distribution (^) Called the stationary distribution of the chain (^) Usually, can only predict a short time out
(^) PageRank over a web graph (^) Each web page is a state (^) Initial distribution: uniform over pages (^) Transitions: (^) With prob. c, uniform jump to a random page (dotted lines) (^) With prob. 1-c, follow a random outlink (solid lines) (^) Stationary distribution (^) Will spend more time on highly reachable pages (^) E.g. many ways to get to the Acrobat Reader download page! (^) Somewhat robust to link spam (^) Google 1.0 returned the set of pages containing all your keywords in decreasing rank, now all search engines use link analysis along with many other factors
sun rain sun rain sun rain sun rain
sun rain sun rain sun rain sun rain