







Study with the several resources on Docsity

Earn points by helping other students or get them with a premium plan


Prepare for your exams
Study with the several resources on Docsity

Earn points to download
Earn points by helping other students or get them with a premium plan
Community
Ask the community for help and clear up your study doubts
Discover the best universities in your country according to Docsity users
Free resources
Download our free guides on studying techniques, anxiety management strategies, and thesis advice from Docsity tutors
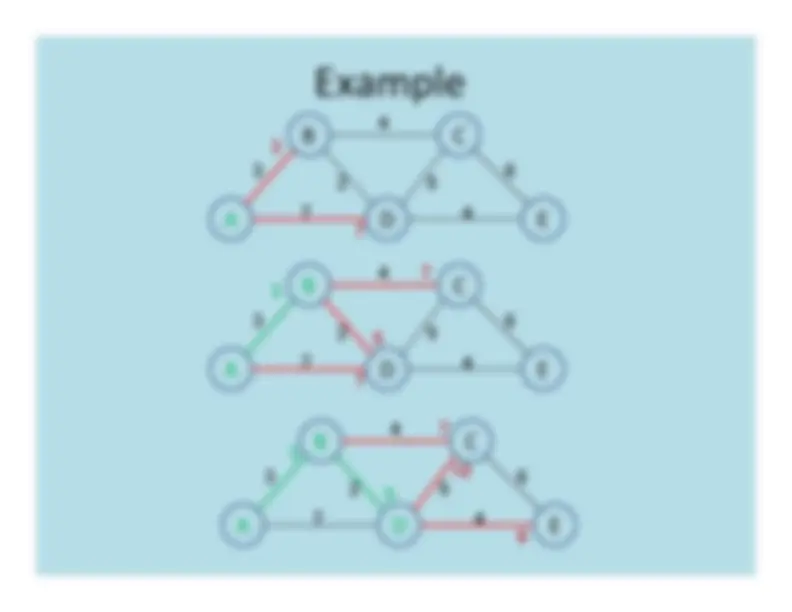
Dijkstra's algorithm is a popular greedy strategy used to find the shortest path between nodes in a weighted connected graph. The concept of greedy techniques, the applications of dijkstra's algorithm, and its working. The algorithm constructs a tree through the graph, where each node in the tree is a node for which the shortest path is already determined. It adds one node to the tree at a time by finding the vertex with the smallest sum of the length of the shortest path from the source and the weight of the edge connecting it to the already selected node. Applications of dijkstra's algorithm include finding optimal solutions for change making, minimum spanning trees, and single-source shortest paths, as well as approximations for the traveling salesman problem and knapsack problem.
Typology: Study notes
1 / 15

This page cannot be seen from the preview
Don't miss anything!










-^ feasible –^ locally
optimal
-^ irrevocable For^ some^
C DB 2 (^6) A^2
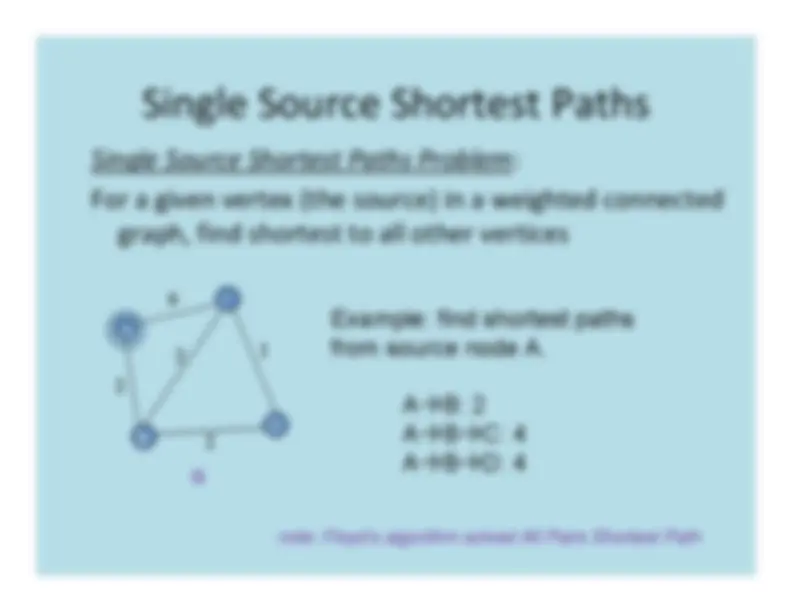
Example: find shortest paths 1 from source node A. G
note: Floyd’s algorithm solved All Pairs Shortest Path
Dijkstra’s
algorithm:
-^ Builds
a^ tree^ through
the^ graph, where^ each
node^ in
the^ tree
is^ a^ node
for^ which
the^ shortest
path^ is^
already^
determined.
-^ Each^
pass^ through
the^ algorithm
adds^ one
node^ to
the^ tree,
by^ finding
vertex^ u
with^ the
smallest
sum^ dv^
+^ w ( v , u
where^ v^ is^ a^ vertex
for^ which
shortest
path^ has
been^ already
found
on^ preceding
iterations
(such^ vertices
form^ a^ tree)
d^ is^ the v^
length^ of
the^ shortest
path^ form
source^
to^ v
w ( v , u )^ is
the^ length
(weight)
of^ edge
from^ v^ to
u
6 2 2 1 C DB 2 (^6) A^2
(^1) G
3
2
5
6 7
4
3
2
5
6 7
(^47) (^57) A
3
2
5
6 7
4 5 3
7 10
9 7 3
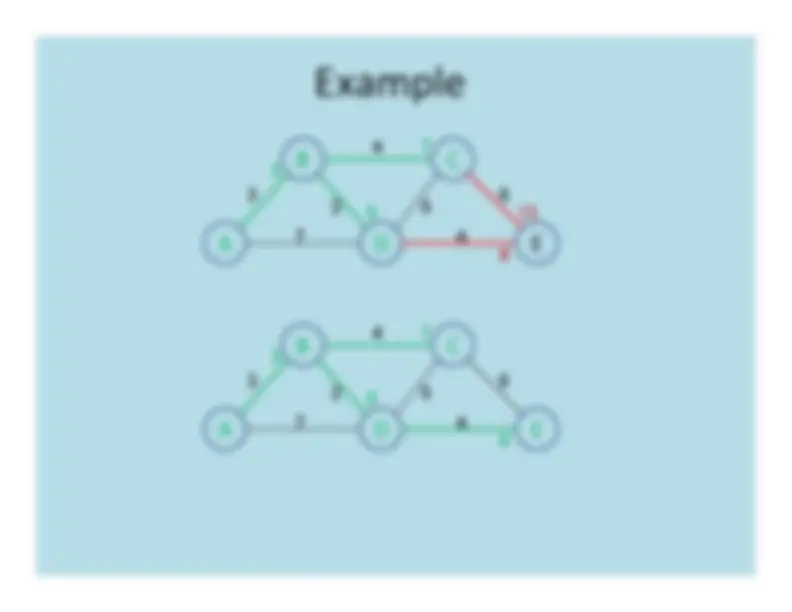
-^ Identify
u*^ =^ fringe
vertex
with^ min
cost
-^ move
u*^ from
fringe
to^ tree
-^ for^ each
fringe
vertex
u^ connected
to^ u*
if^ d^ +w(u,u)u^
<^ d^ :u^ p^ =^ uu^ d^ =^ d^ u^ u
+w(u*,u)
Tree^
Remaining vertices a(-,0)^
b(a,3) c(-,
∞) d(a,7) e(-,
b(a,3)^
c(b,3+4) d(b,3+2) e(-,
d(b,5)^
c(b,7)^
e(d,5+4) c(b,7)^
e(d,9) e(d,9)
b a 4 c d
e 3 7
(^62 ) b a 4 c d
e 3 7
(^652 ) b a 4 c d
e 3 7
(^4) d 62 5 4 b^ a 4
e 3 7
6 c 2 5 d (^4) bc ad e 3 7
(^652 )
-^ Doesn’t
work^
for^ graphs
with^
negative
weights • Applicable
to^ both
undirected
and^ directed
graphs • Efficiency^ –^ O(|V|
2 )^ for^ graphs
represented
by^ weight
matrix
and^ array
implementation
of^ priority
queue
-^ O(|E|log|V|)
for^ graphs
represented
by^ adj.^ lists
and^ min
‐heap^ implementation
of^ priority
queue
BFS :^ visit
all^ nodes
-^ adj^ matrix:
adj^ list:^
-^ TSP^ (Brute
Force):^
shortest
tour
-^ O(n!) • Warshall
(DP):^ transitive
closure
Floyd^ (DP):
all^ pairs
shortest
path (^3) – Θ(|V
-^ Prim^
(greedy):
minimum
spanning
tree
Dijkstra
(greedy):
single^ source
shortest
path
-^ matrix/array:
list/heap:
O(|E|log|V|)
-^ Kruskal
(greedy):
minimum
spanning
tree
-^ O(|E|log|E|)