







Study with the several resources on Docsity

Earn points by helping other students or get them with a premium plan


Prepare for your exams
Study with the several resources on Docsity

Earn points to download
Earn points by helping other students or get them with a premium plan
Community
Ask the community for help and clear up your study doubts
Discover the best universities in your country according to Docsity users
Free resources
Download our free guides on studying techniques, anxiety management strategies, and thesis advice from Docsity tutors
Main points of this past exam paper are: Balloon Catheter Design, Design, Circumferential Stress, Thin-Walled High Pressure, Inflation, Internal Pressure, Tensile Forces, Dilation Fluid, Resist Bursting, Longitudinal Stress
Typology: Exams
1 / 11

This page cannot be seen from the preview
Don't miss anything!







Exam Code(s) 4BG
Exam(s) 4 th Engineering – Biomedical
Module Code(s) ME
Module(s) Medical Implant and Device Design
Paper No. I
External
Examiner(s)
Professor David Taylor
Internal
Examiner(s)
Professor Peter McHugh
Dr. Laoise McNamara
Dr. Patrick McGarry
Instructions: Answer 5 questions.
All questions will be marked equally.
Use a separate answer book for each section.
Duration 3hrs
No. of Pages 11
Department(s) Mechanical and Biomedical Engineering
Requirements Statistical Tables
Graph Paper
Log Graph Paper
Other Material
Release to Library: Yes
Question 1:
(a) Identify the two main classifications of balloon catheter design and the features of
the design that provide the main function. ( 3 )
(b) Derive an expression for the circumferential stress in a thin-walled high pressure
balloon catheter device during inflation if the balloon has an internal pressure, p,
exerted from the dilation fluid (Figure 1a), and experiences tensile forces that
resist bursting (Figure 1b). ( 6 )
Figure 1(a) Figure 1(b) Figure 1(c)
(c) Derive an expression for the longitudinal stress in the balloon (Figure 1c) (5)
(d) An angioplasty balloon is designed to have a length of 20mm, a wall thickness of
0.05mm and the diameter of the balloon when it is inflated is 5. 8 mm. The balloon
is made from Polyethylene terephthalate (PET), which has a tensile modulus of
4GPa and a Poisson’s ratio of 0.37. Calculate the maximum strain in the axial and
circumferential directions if an internal pressure of 17 atm is required to dilate a
stenosed artery. (5)
(e) If PET is plastically deformed above 2% strain, will it be safe to operate the
balloon to dilate the stenosis? ( 1 )
Question 3 :
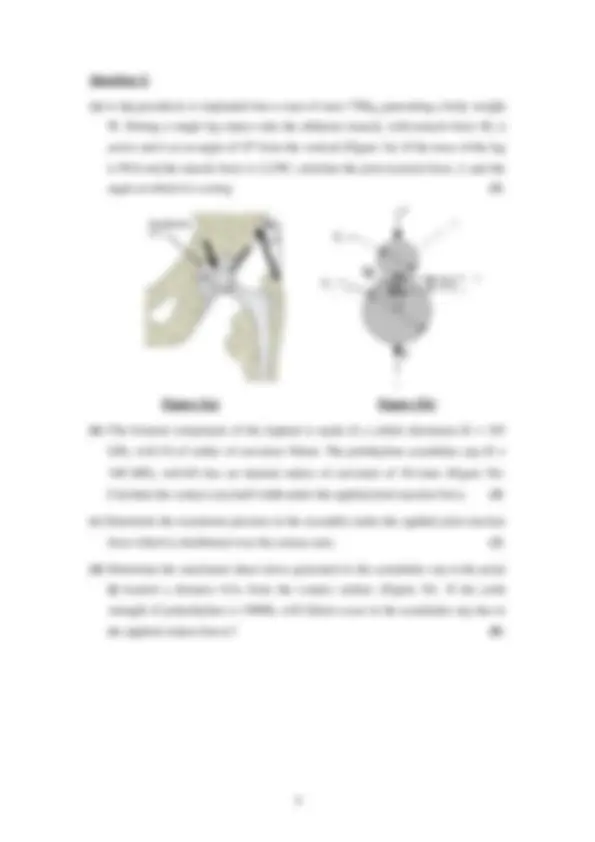
(a) A hip prosthesis is implanted into a man of mass 75Kg, generating a body weight
W. During a single leg stance only the abductor muscle, with muscle force M, is
active and is at an angle of 35º from the vertical (Figure 3a). If the mass of the leg
is W/6 and the muscle force is 2.22W, calculate the joint reaction force, J, and the
angle at which it is acting. (5)
Figure 3 (a) Figure 3 (b)
(b) The femoral component of the implant is made of a cobalt chromium (E = 105
GPa, =0.3 3 ) of radius of curvature 58 mm. The polethylene acetabular cup (E =
190 MPa, =0.4 5 ) has an internal radius of curvature of 58 .1mm (Figure 3b).
Calculate the contact area half width under the applied joint reaction force. (4)
(c) Determine the maximum pressure in the assembly under the applied joint reaction
force which is distributed over the contact area. ( 2 )
(d) Determine the maximum shear stress generated in the acetabular cup at the point
Q located a distance 0.5 a from the contact surface (Figure 3 b). If the yield
strength of polyethylene is 19 MPa, will failure occur in the acetabular cup due to
the applied contact forces? ( 8 )
0.5 a
Question 4 :
(a) What are the goals of fracture fixation and what medical devices are used to
encourage fracture fixation? (3)
(b) A fracture fixation plate is implanted to encourage fracture healing in a patient
(Figure 4a). It is anticipated that the plate will be subject to a bending load, M, of
35 Nm. The plate has a width, W, of 2 5mm, the thickness, h, of the plate is 6 mm
and there are bolt holes in the plate for bone screws of diameter, d, 12 mm (Figure
4b). Find the stress concentration factor caused by the bolt hole on the fracture
fixation plate. ( 5 )
Figure 4 (a) Figure 4 (b)
(c) Compute the maximum stress in the plate by taking into account the stress
concentration caused by a transverse hole in flat plate in bending. ( 5 )
(d) If the plate in Figure 4 (a) is redesigned to have a thickness, h, of 10 mm, what
effect will this have on the stress concentration factor? ( 6 )
(e) Compute the maximum stress in the revised design of the fixation plate. ( 3 )
h
d
w
Question 6 :
(a) For plane stress (zero out-of plane stress components, i.e.zz = xz = xz = 0)
write down expressions, in terms of xx, yy and xy, for the von Mises yield
criterion. (2)
Figure 6
(b) Figure 6 shows an NIR 316L stainless steel stent unit cell following balloon
deployment to a diameter of 2mm. The recommended deployment diameter is
3mm. The stresses at three points in the stent, A, B and C, are given as:
A: xx=-300MPa yy= 0MPa xy=90MPa
B: xx= 0MPa yy=300MPa xy= 0MPa
C: xx= 150MPa yy= 10MPa xy=50MPa
The yield stress of 316L stainless steel is 240MPa. Using the von Mises yield
criterion determine if plastic yielding occurs at points A, B and C. ( 5 )
Comment on the effectiveness of the stent design. (1)
(c) At the end of the systole the stress state at point A (Figure 1) is
xx=-310MPa yy= 5MPa xy=95MPa
At the end of diastole the stress at the same point is
xx=-300MPa yy= 0MPa xy=0MPa
The Paris equation for the rate of fatigue crack growth is given as
B
A
C
m C K
dN
da
where a is the crack length, N is the number of cycles, K is the change in the
stress intensity factor and C and m are material parameter constants.
For 316L stainless steel m =3.4 and C =1.2x
used for crack length and stress respectively. If the stent contains a crack of length
0.5m at point A, determine the number of cardiac cycles before the crack grows
to a length of 50m. (1 1 )
Are FDA guidelines for fatigue life satisfied? (1)
Table 1: Area and stress relationships for contact between elastic bodies
3
1 2
2
2
2
1
2 1
d d
a
2
2
1
max
1 tan
a
z a
a^ z
z
p x y
1 2
2
2
2
1
2
1
d d
l
b
b
z
b
z
p x (^) 2
2
max
b
z
b
z
b
z
p y
2
2
2
max (^2)
2
2
max
b
z
p
z