Download Temperature Dependence of van't Hoff Equation and Equilibrium Constant and more Study notes Physical Chemistry in PDF only on Docsity!
Lecture 22 Chapter 13 & 14 – Extent of reaction and equilibrium
Remember next exam is 1 week from Friday. Today will be last quiz before exam. GRE practice today
Outline :
van’t Hoff partition function phase diagrams
Review
∆ mix G =? nRT(XA ln X (^) A + XB ln XB )
G
Greact
Gprod
∆GMix
∆GRxn
∆GTot
ξ
without mixing
Recall we looked at N 2 O 4 Æ 2NO 2
N 2 O 4 (g) <-> 2 NO 2 (g)
Initial amounts 1 0 Equilibrium amounts (^) 1 - ξ 2 ξ Total amount = 1 + ξ Equilibrium mole fractions (^) (1 - ξ)/(1 + ξ) 2 ξ/(1 + ξ)
( ) {[ ] }
2
(^22)
2 4
2 2 2 4
2 2 1
[( 1 )/( 1 )]
reactants
products ξ
ξ ξ ξ
ξ ξ −
− + ×
+ ×
P
P
P
X P
X P
P
P
K
NO Tot
NO Tot NO
NO p
Solving for ξ 2
1 [ 1 ( 4 /K)P]
ξ=
OK then to clarify from last time: The equilibrium constant is constant ONLY with respect to concentration. In the case above we are using pressure to measure concentration so K is constant w.r.t. pressure, but not Temperature.
So, when we see ∆rG^0 = - RT ln K the ∆rG^0 must be constant; T and K both move to balance each other.
Response of equilibria to temperature
We can use Le Chatelier’s principle to guide what to expect for temperature dependence.
Exothermic reactions generate heat Æ heat is one of the products. So if we increase the temperature? The equilibrium will shift to make less heat (less products).
Endothermic reactions absorb heat Æ heat is a reactant. If we increase T, we can expect that the equilibrium will shift to absorb more heat (more products).
OK, so now we are going to do a little derivation in that direction. (FAST) Recall that ∆rG^0 = - RT ln K
so R K T
r G ln
0 = −
Recall also that ∆G = ∆H - T∆S or ∆G^0 /T = ∆H^0 /T - ∆S^0 If we take a derivative wrt T:
T^2
H
T
G
T
r p
r
(Hº and Sº do not depend on T)
substitute for G^0.
2
ln T
H
dT
d R K ∆ r^ ∅
A little cleanup gives us the van’t Hoff (a Dutch guy) equation:
d K dT
H
RT
ln (^) = r
∆^ ∅
2 or in a different form that is sometimes more convenient:
d K d T)
H
R
ln r ( / 1
∆^ ∅
We can see from the first form of the van’t Hoff equation that if a reaction is exothermic (∆H < 0), d ln K/ dT will be negative. Therefore as the temperature rises, K will become smaller. Similarly, if the reaction is endothermic (∆H > 0), K will increase as the temperature is raised.
Stop for a second and think about what this means… Draw version of Figure 13. Population will distribute itself among all energy states of the system according to Boltzmann, irrespective of the molecular identities.
Okay, then let’s get back to K. Recognizing that concentration is N/V
b B
a A
z Z
y Y
c
V
q V
q
V
q V
q
K T
Of course qi = qtrans qrot qvib qelec for each species i in the chemical reaction
For the H 2 + I 2 -> 2 HI reaction we have
2 2 2 2
2
2
H I
HI H I
HI
c q q
q
V
q V
q
V
q
K T =
the expression is ( similar to example 13.2 in Dill )
RT
2 D D D /T 2
/T /T HI^2 rot
I 2 rot
H 2 rot
3 / 2
H 2 I 2
2 HI c
HI 0 H 02 I 02 HIvib
Hvib 2 Ivib 2 e ( 1 e )
4 ( 1 e )( 1 e ) m m
m K (T)
− − −Θ
−Θ −Θ
−
translational rotational vibrational electronic
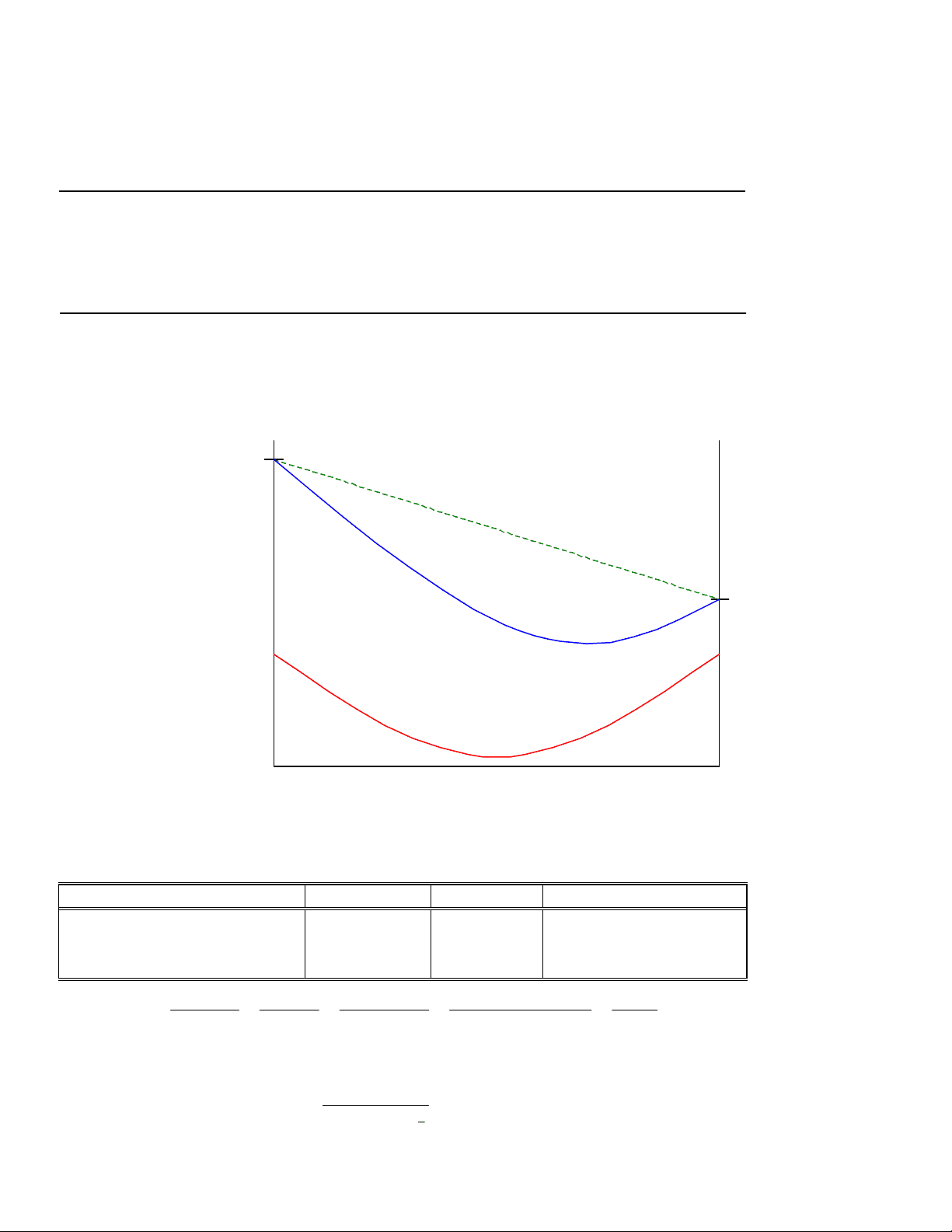
Where is our T dependence? Only in the vibrational and electronic parts of the expression, and the biggest contributor is vibrational part again! (With our usual approximation that T >> ΘRot )
Let’s look at how K changes as temp changes. As T increases, the exponential term goes toward 1 and (1- exponential) goes toward zero. A big Θvib means that the (1-exp) term decreases more slowly. So, if reactant Θvib > product Θvib then numerator (reactant) decreases more slowly than denominator (product): therefore, K increases as T increases.
Because Θvib = hν/kB and ν = 1/2π (k/μ) 1/ -> Θvib is proportional to k (force constant)
So, if product has weaker bonds than reactant, than indeed: reactant Θvib > product Θvib and K increases with temp – just like endothermic reaction – makes sense if product bonds are weak! Stronger bonds are more stable than weaker ones – weak bonds are higher in energy than strong ones.
The reverse (K decreases with increasing T) is the case for the H 2 + I 2 -> 2HI reaction, since the HI bond is modest but the I 2 bond is very weak. Note that the weak I 2 bond offsets the relatively strong H 2 bond.
Note that the book example uses H 2 and D 2 going to 2HD, so bond strengths are basically identical. The important thing then is the factor of 4 coming from rotational symmetries.
Okay then next time we’ll move into chapter 14, where we get into phase equilibria. I will not be describing his liquids lattice model today, but we will be using it in the future. So, please please please read through it carefully. It is a little long, but he explains things thoroughly I think.
Vibrational contributions to equilibrium constant
0
1
0 500 1000 1500 2000 2500 3000 3500 4000 Temperature (K)
H2 contribution I2 contribution HI contribution Total vibrational contribution
